Сложение движений твердого тела в теоретической механике

Содержание:

Сложение движений твердого тела:

Во многих вопросах техники приходится встречаться со случаями, когда твердое тело участвует в нескольких движениях. Совокупность всех движений твердого тела, как будет показано ниже, может быть сведена к двум простым движениям — поступательному и вращательному вокруг некоторой оси.

Рассмотрим следующие случаи сложения движений твердого тела.

1. Сложение двух поступательных движений тела. Нетрудно видеть, что этот случай движения тела сводится к сложению движений точки.
2. Сложение вращательного движения с поступательным, происходящим перпендикулярно к оси вращения.

Пусть тело (рис. 224) вращается с угловой скоростью

Так как переносная и относительная скорост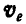и и 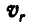направлены по одной прямой в противоположные стороны, а относительная скорость зависит от расстояния 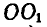и равна 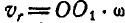, то можно подобрать такое положение точки 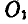когда будет выполнено равенство 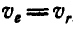, или, что то же самое, когда расстояние 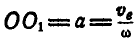, а следовательно, и вся прямая, проходящая через перпендикулярно к плоскости чертежа, будет в данный момент неподвижной. Поэтому тело будет вращаться около этой мгновенной оси с угловой скоростью:

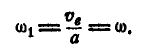
Итак, вращательное движение и поступательное в плоскости, перпендикулярной к оси вращения, складываются в одно вращательное движение с прежней угловой скоростью вокруг оси , параллельной данной оси О и отстоящей от нее на расстоянии .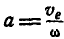

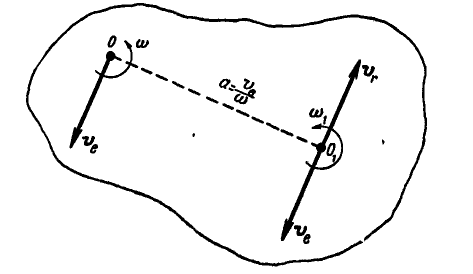
Рис. 224.

Ясно, что положение мгновенной оси 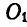будет непрерывно меняться.

Делая обратный переход от мгновенной оси 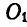к какой-либо другой оси О, заключаем, что ось вращения можно переносить параллельно самой себе, прибавив при этом поступательное движение со скоростью, равной произведению угловой скорости на расстояние между осями. Важно отметить, что угловая скорость 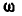от выбора оси не зависит.

3. Сложение двух вращательных движений вокруг параллельных осей. В качестве иллюстрации такого движения представим себе диск А (рис. 225), вращающийся вокруг вертикальной оси с угловой скоростью 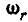. Пусть ось вращения диска проходит через линейку В, которая, в свою очередь, вращается вокруг неподвижной вертикальной оси с угловой скоростью 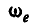. Таким образом, диск А участвует в сложном вращении — с одной стороны, он совершает относительное вращательное движение по отношению к линейке с угловой скоростью 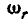, а с другой — переносное вращательное движение вместе с линейкой с угловой скоростью 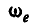. При этом относительное и переносное вращательные движения диска могут происходить в одну сторону и в противоположные стороны (на рисунке 225 вращения происходят в одну сторону).

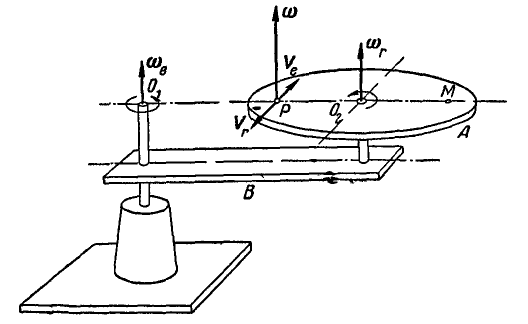
Рис. 225.

В качестве диска и линейки мы можем представить себе две неограниченные фигуры, совершающие свое вращательное движение в плоскости чертежа (рис. 226).

Соединяя точки 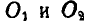прямой 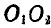, замечаем, что любая точка Р, расположенная на этой прямой и принадлежащая плоскости А (диску), будет иметь абсолютную скорость, равную разности относительной и переносной скоростей 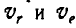, которые эта точка получает вследствие вращения диска вокруг осей 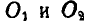. Всегда можно найти такую точку Р, для которой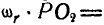 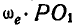; в таком случае эта точка окажется в данный момент неподвижной, а следовательно, плоскую фигуру А (диск) можно рассматривать, как вращающуюся мгновенно вокруг этой оси.

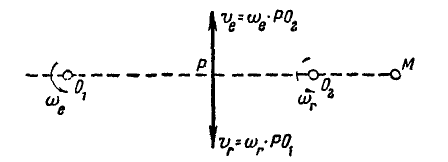
Рис. 226.

Итак, два вращения вокруг параллельных осей складываются в одно вращение вокруг оси, параллельной данным и отстоящей от них на расстояниях, обратно пропорциональных угловым скоростям составляющих вращений, т. е.:

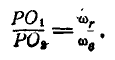
Ось этого вращения будет мгновенной осью, так как в следующий момент ось 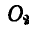переместится и прямая 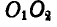займет другое положение.

Для определения мгновенной угловой скорости 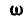абсолютного вращения плоскости А (диска) вокруг оси Р возьмем какую-либо точку М плоскости А;  скорость этой точки может быть, с одной стороны, выражена через произведение 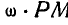, но, с другой стороны, та же скорость может быть записана в виде: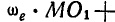 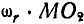 и, следовательно, .

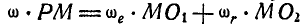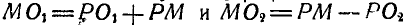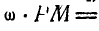
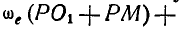
Подставляя значение , а также имея в виду, что находим: 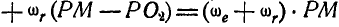. Отсюда:

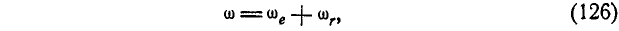
т. е. угловая скорость мгновенного вращения равна сумме угловых скоростей относительного и переноского вращений.

Изобразив угловые скорости относительного, переносного и абсолютного вращений в виде векторов 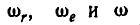(рис. 225), замечаем, что эти векторы, параллельные между собой, складываются по тем же правилам, как и параллельные силы. Отсюда следует, что два вращения, происходящие вокруг параллельных осей в противоположные стороны (рис. 227), складываются в одно вращение вокруг оси Р, лежащей за осью с большей угловой скоростью; при этом мгновенная угловая скорость абсолютного вращения .

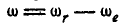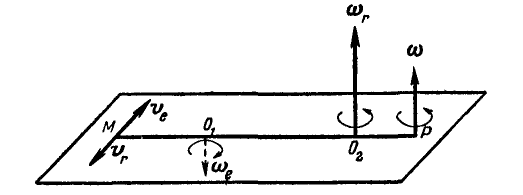
Рис. 227.

В приведенных выше случаях сложения вращений мы видим, что три центра —переносный 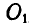относительный 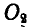и абсолютный Р (рис. 225, 226 и 227) — всегда лежат на одной прямой.

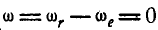Если , то в этом случае , и движение будет только поступательным. Линейная скорость любой точки М этого движения (рис. 227) будет:

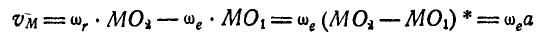
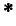Так как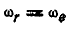

и будет одинаковой для всех точек фигуры, участвующей в двух вращениях и совершающей поступательное движение в плоскости, перпендикулярной к осям вращения.

Обратно, всякое поступательное движение можно заменить двумя вращательными. Такая совокупность вращений называется парой вращений.

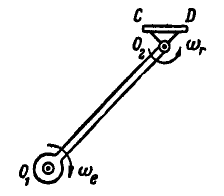
Рис. 228.

В качестве примера пары вращений может служить педаль велосипедного колеса (рис. 228), которая за полный оборот кривошипа совершает вокруг своей оси 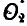тоже полный оборот, но в противоположную сторону, в силу того, что 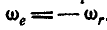. Сама же педаль совершает поступательное движение, так как плоскость CD все время сохраняет свое горизонтальное положение.

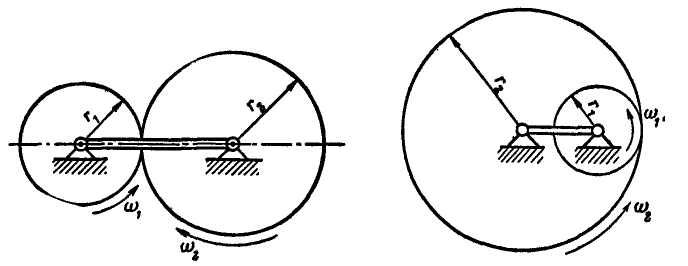
Рис. 229.                                                             Рис. 230.

Переходя к решению задач, условимся считать угловую скорость вращения против часовой стрелки положительной, а в обратную сторону — отрицательной. Кроме того, при неподвижных осях вращения колес полезно иметь в виду следующие очевидные равенства:

для внешнего зацепления колес (рис. 229)

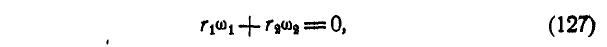
для внутреннего зацепления колес (рис. 230)

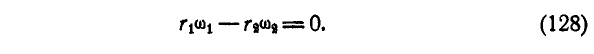
Задача №1

Маховик радиусом 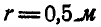вращается вокруг оси О, делая 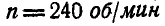(рис. 231).

Не изменяя характера движения маховика, перенести ось вращения его параллельно самой себе в положение .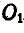

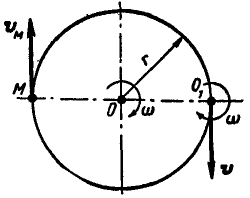
Рис. 231.

Решение. Мы знаем, что при параллельном переносе оси вращения из положения 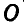в 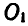маховик будет вращаться вокруг новой оси 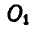с прежней угловой скоростью:

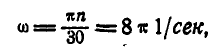
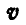но при этом сама ось вращения получит скорость  поступательного движения, равную:

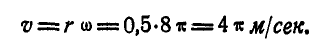
Нетрудно видеть, что скорость любой точки М маховика по отношению к осям вращения О и будет одинаковой:

Задача №2

На палец А кривошипа OA (рис. 232, а) свободно насажено зубчатое колесо II радиуса 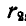, сцепленное с зубчатым колесом I радиуса 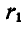имеющим неподвижную ось О. Определить абсолютную угловую скорость 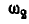, колеса II, если кривошип и колесо I вращаются с угловыми скоростями, соответственно равными .

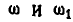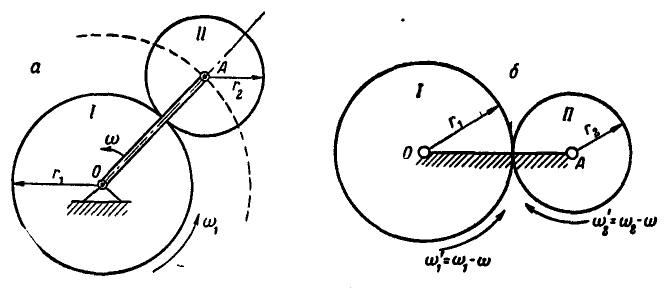
Рис. 232.

Решение. Найдем угловые скорости 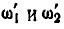вращения колес I и II относительно кривошипа OA, для чего следует мысленно встать на кривошип, или, что то же, закрепить кривошип OA неподвижно, сообщив для этого всей системе угловую скорость  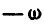(рис. 232, б). Тогда относительные угловые скорости сцепленных между собой колес I и II будут: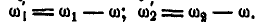

Так как зацепление колес внешнее, то по формуле (127) имеем: 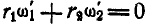, или 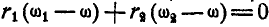, откуда

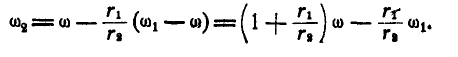
Если колесо I вращается в сторону, обратную вращению кривошипа, то 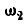увеличивается, так как 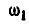будет иметь уже отрицательное значение. В этом случае:

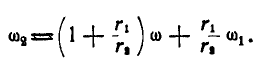
В частности, при неподвижном колесе I его угловая скорость 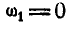и, следовательно: ,

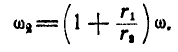
Задача №3

На неподвижной оси (рис. 233) насажены свободно два колеса I и III радиусами 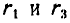и рама ОАВО.

На ось АВ рамы свободно насажены колеса II и IV радиусами 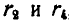, неизменно связанные между собой и находящиеся в зацеплении с колесами I и III. Определить угловую скорость  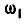первого колеса, если известны угловые скорости рамы 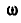и колеса  .

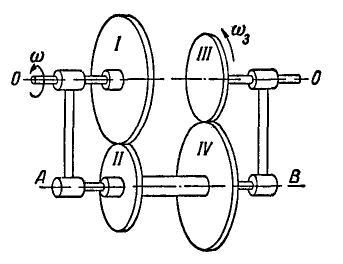
Рис. 233.

Решение. Найдем угловые скорости колес относительно рамы, для чего мысленно встанем на раму и будем двигаться вместе с нею.

Тогда относительные угловые скорости колес I, II и III будут: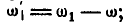   

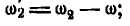
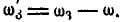
С другой стороны, на основании уравнения (127) находим: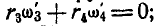  

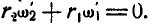
Исключая из последних двух равенств 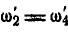, имеем: .

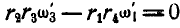Или

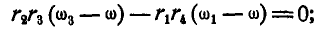
откуда

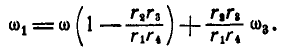
Если 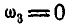, то:

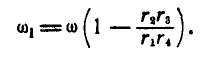
Задача №4

Механизм конного привода (рис. 234) состоит из большого зубчатого колеса I радиусом 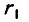, с направленными внутрь зубцами. В центре этого колеса укреплена ось А, на которую насажено зубчатое колесо III радиусом 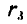, и водило АВ. На водиле имеется ось О, на которую насажено колесо II радиусом 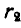, находящееся во внешнем зацеплении с колесом III и во внутреннем — с колесом I.

Определить абсолютную угловую скорость вращения 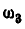, колеса III, если угловые скорости колеса I и водила соответственно равны .

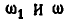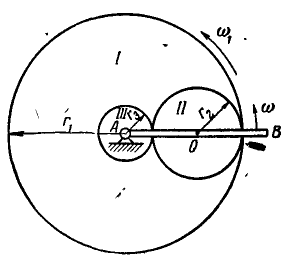
Рис. 234.

Указание: Находим угловые скорости колес I, II и III относительно водила: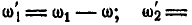

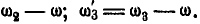
Далее на основании формул (127) и (128) имеем: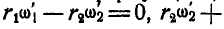

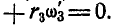
Ответ: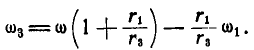

Задача №5

Найти число оборотов в минуту шестерни с числом зубцов 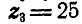(рис. 235), если кривошип ОА вращается вокруг оси О неподвижной шестерни с угловой скоростью, соответствующей 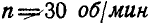, и несет на себе ось двойной шестерни с числом зубцов  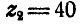и .

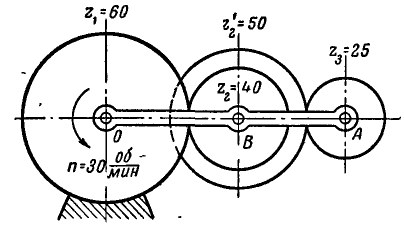
Рис. 235.

Решение. Обозначив число оборотов в минуту колес соответственно через 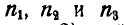 (по условию 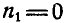), найдем число оборотов в минуту колес относительно кривошипа ОА:  

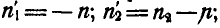
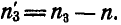
Считая, что при одинаковом модуле зацепления колес числа зубцов их пропорциональны радиусам, на основании равенства (127) имеем: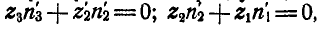 или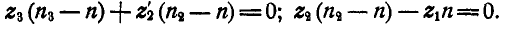

Мы получили систему двух уравнений с двумя неизвестными 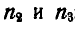; решая их, найдем:

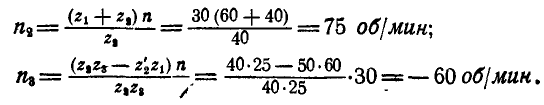
Задача №6

Редуктор скоростей с дифференциальной передачей состоит из четырех зубчатых колес (рис. 236), из которых первое — с внутренним зацеплением — делает 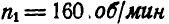и имеет 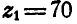зубцов; второе и третье спарены между собой и сидят на оси, соединенной жестко с осью ведущего вала I, совершающего 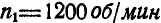; числа зубцов 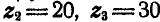; четвертое — с внутренним зацеплением — имеет 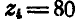зубцов и заклинено на ведомом валу II. Найти число оборотов в минуту ведомого вала, если вал I и колесо I вращаются, в противоположных направлениях.

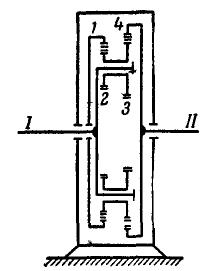
Рис. 236.

Решение. Пусть числа оборотов в минуту колес 1, 2, 3 и 4 будут 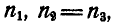, 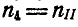и водила 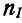. Числа оборотов в минуту колес относительно водила будут:

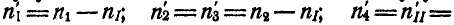
На основании равенства (128) можем написать: 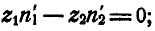 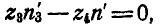или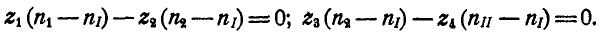 

Решая полученные уравнения относительно 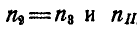, найдем:    

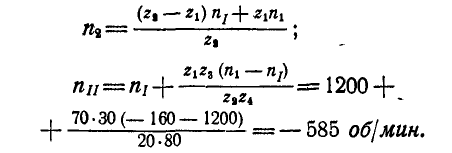
4. Сложение вращений вокруг пересекающихся осей.

Пусть диск А (рис. 237, а) вращается вокруг оси OD с относительной угловой скоростьй 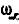; сама же ось OD, в свою очередь, вращается вокруг оси ОВ с переносной угловой скоростью 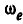. Изобразив угловые скорости  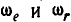в виде векторов, построим на них параллелограмм OBCD (рис. 237, б).

Определим скорость точки С, связав ее мысленно с диском А. Эта точка в результате вращения вокруг осей OD и ОВ будет иметь относительную и переносную скорости 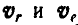, направленные перпендикулярно к плоскости параллелограмма OBCD. Величины этих скоростей соответственно равны:

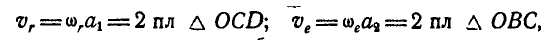
но-так как , то 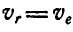, т. е. точка С в данный момент неподвижна.

Кроме точки С, имеется еще неподвижная точка О, поэтому неподвижной в данный момент будет вся прямая ОС.

Итак, два вращения, происходящие вокруг пересекающихсяосей, складываются водно вращение, происходящее вокруг мгновенной оси, совпадающей с диагональю параллелограмма, построенного на векторах относительной и переносной угловых скоростей.

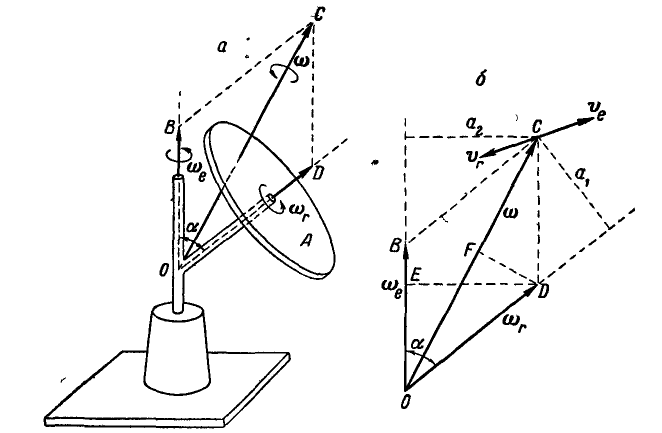
Рис. 237.

Легко показать, что абсолютная угловая скорость мгновенного вращения равна геометрической сумме относительной и переносной угловых скоростей:

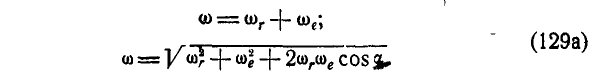
Это следует из того, что, определяя скорость точки D относительно осей ОВ и ОС, мы можем написать:

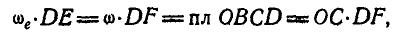
откуда

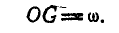
Задача №7

Дифференциал состоит из двух одинаковых зубчатых конических колес I и II, свободно насаженных на горизонтальную ось (рис. 238). С горизонтальной осбю наглухо скреплена перпендикулярная к ней ось, на которую свободно насажено коническое колесо III, сцепленной с колесами I и II. Зная, что колеса I к II имеют угловые скорости, равные 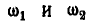, определить угловую скорость оси 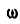и угловую скорость  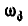вращения колеса III вокруг своей оси.

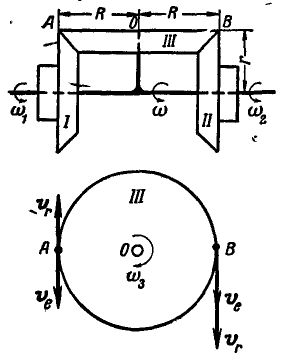
Рис. 238.

Решение. Абсолютные скорости точек обода А и В колес I и II соответственно равны: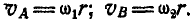

С другой стороны, отнеся эти точки к колесу III, можем сказать, что абсолютные скорости этих точек найдутся путем суммирования переносной скорости 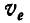центра О колеса III и относительной скорости 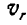получающейся вследствие вращения колеса III около этого центра.

Полагая для определенности имеем:

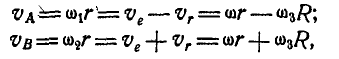
откуда находим:

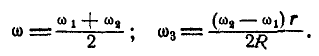
Задача №8

Коническое колесо радиусом 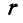обегает пять раз в минуту окружность радиуса R, оставаясь наклоненным к ее плоскости под углом 60° (рис. 239). Вычислить угловую скорость 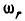колеса вокруг его оси и угловую скорость 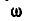вращения вокруг мгновенной оси.

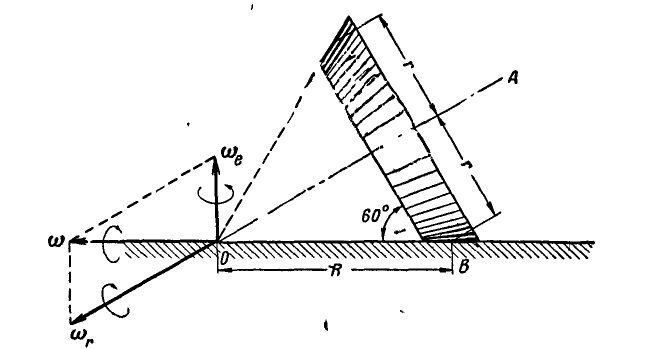
Рис. 239.

Решение. Движение колеса можно рассматривать, как вращение, происходящее вокруг вертикальной оси с переносной угловой скоростью 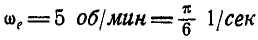и одновременно вокруг его оси ОА с неизвестной относительной угловой скоростью 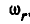. Оба упомянутых вращения могут быть заменены одним, а именно вращением вокруг мгновенной оси ОВ с угловой скоростью 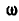, определяемой равенством (129):   

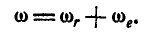
Построив параллелограмм векторов угловых скоростей, находим:

• Заказать решение задач по теоретической механике

Задача №9

Шаровая дробилка состоит из полого шара II, сидящего на оси CD, на которой заклинено коническое зубчатое колесо D радиусом 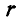. Ось CD сидит в подшипниках в раме I, составляющей одно целое с осью АВ и приводящейся во вращение при помощи рукоятки F. Колесо D сцепляется с неподвижным колесом Е радиусом R. Определить абсолютную угловую скорость шаровой дробилки 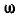и абсолютное угловое ускорение 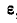, если рукоятка вращается с постоянной угловой скоростью 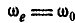; угол между осями АВ и CD равен 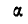(рис. 240).

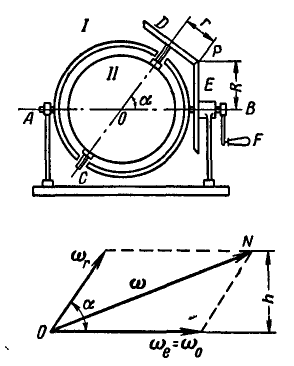
Рис. 240.

Решение. Колесо D, катясь без скольжения по неподвижному колесу Е, имеет полюс мгновенного вращения в точке Р касания колес. Следовательно, ось мгновенного вращения колеса D совпадает с прямой ОР. На основании этого построим параллелограмм угловых скоростей (рис. 240, внизу).

Для нахождения соотношения между 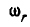 и 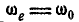сообщим всей системе угловую скорость 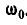. Тогда ось CD дробилки будет неподвижной, а неподвижное колесо Е начнет вращаться с угловой скоростью 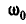. Оси конических колес D и Е будут неподвижны и, следовательно, можно применить равенство (127):

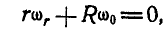
откуда

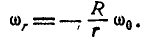
Из чертежа имеем:

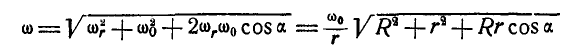
Вектор углового ускорения , как было показано выше, представляет скорость точки N — конца вектора , а поэтому:

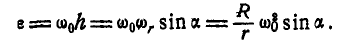
6. Сложение вращательного движения и поступательного, образующего с осью вращения любой угол. Пусть тело вращается вокруг оси О с угловой скоростью , сама же ось движется поступательно со скоростью 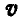, образующей с осью вращения угол 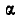(рис. 241). Разложим скорость 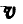на две составляющие: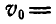 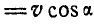, направленную по оси вращения, и 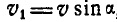, перпендикулярную к оси.

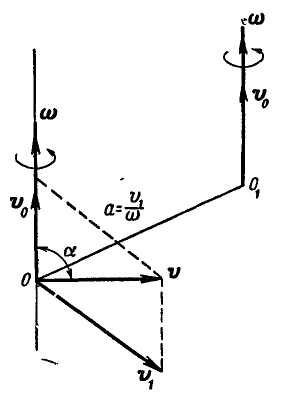
Рис. 241.

Совокупность движений 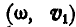, согласно случаю 2, может быть заменена одним вращением вокруг оси 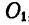параллельной оси О, с той же угловой скоростью, и отстоящей от оси О на расстоянии:

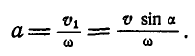
Скорость поступательного движения 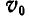может быть перенесена параллельно самой себе на ось .

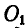Итак, вращательное движение и любое поступательное движение приводятся к вращательному движению с угловой, скоростью 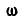вокруг оси 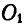и поступательному— вдоль этой оси. Такая совокупность более не упрощается и называется винтовым движением.

Все рассмотренные нами случаи являются частными этого общего случая.

Задача №10

Тело участвует в двух вращениях, происходящих с угловыми скоростями 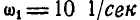 и 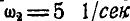вокруг непересекающихся осей 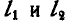, (рис. 242, а). Кратчайшее расстояние между осями 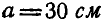. Привести данное движение тела к винтовому движению.

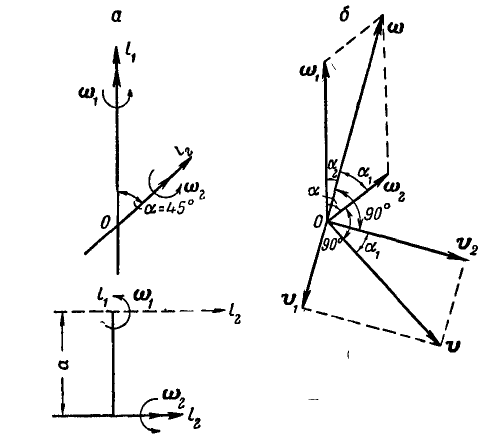
Рис. 242.

Решение. Перенесем ось 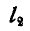 параллельно самой себе в точку О, добавив при этом скорость поступательного движения 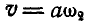. Сложив по правилу параллелограмма угловые скорост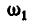и  и 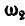, разложим скорость поступательного движения на две составляющие, из которых одна составляющая, равная 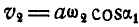, перпендикулярна к 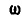, другая  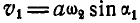— направлена вдоль вектора 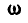(рис. 242, б). Совокупность движений 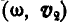может быть заменена одним вращением с угловой скоростью 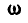вокруг мгновенной оси, параллельной 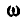и отстоящей от нее на расстоянии 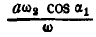. Итак, вращение тела вокруг непересекающихся осей привелось к винтовому движению, происходящему вокруг мгновенной оси, с угловой скоростью:

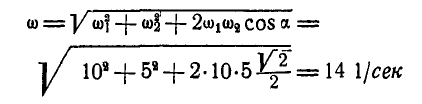
поступательного движения, направленной вдоль оси:

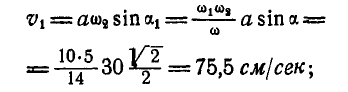
при этом мгновенная ось винтового движения отстоит от оси А на расстоянии:

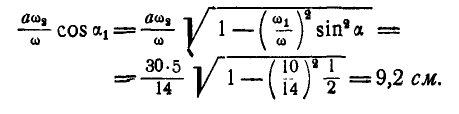
Сложение движений твердого тела

Сложение двух поступательных движений одного тела приводит к поступательному движению

Сложение поступательных движений

Изучив теоремы сложения скоростей и ускорений точки, заметим, что движение не только точки, но и тела часто приходится рассматривать как составное. Более сложные случаи составного движения тела, а именно сложение поступательного и вращательного движений и сложение поступательного и сферического мы будем изучать в следующих параграфах, а здесь коснемся лишь сложения скоростей при простейших движениях тела.

В случае поступательного движения тела все точки имеют одинаковые скорости, и движение любой из точек тела вполне характеризует движение всех остальных. Если телу сообщено не одно, а одновременно два или несколько поступательных движений, то все его точки продолжают находиться в совершенно идентичных условиях, параллелограммы скоростей всех точек одинаковы, так же как и параллелограммы ускорений, и тело совершает поступательное движение.

Угловые скорости складывают по правилам геометрического сложения

Сложение угловых скоростей

Пусть некоторое твердое тело (рис. 129) вращается с угловой скоростью ω_r вокруг оси OR, в то время как эта ось поворачивается вокруг оси OE с угловой скоростью ω_e. Представим эти угловые скорости в виде векторов OA и OB, отложенных по осям, и построим на них параллелограмм OACB. Легко показать, что скорости  точек тела, лежащих на диагонали ОС, равны нулю. В самом деле, точка C обладает двумя скоростями: относительной υ_r = ω_rCM, направленной перпендикулярно к чертежу на читателя, и переносной υe = ω_eCN, направленной в противоположную сторону. Но ω_rCM = ω_eCN, так как оба эти произведения выражают площадь одного и того же параллелограмма OACB. Следовательно, скорость точки C равна нулю, как и скорость точки О, находящейся на пересечении осей OR и OE. Отсюда заключаем, что мгновенная ось вращения совпадает с диагональю параллелограмма угловых скоростей.

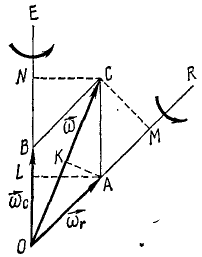
Рис. 129

Определим теперь угловую скорость ω тела при составном вращении вокруг этой оси ОС. Для этого удобно взять точку А. Скорость точки А в относительном движении тела вокруг оси OR равна нулю, а в переносном вращении вокруг оси OE равна ω_eAL. Но ω_eAL выражает площадь параллелограмма OACB и может быть представлена как произведение OC ^. AK, где AK—расстояние точки тела от мгновенной оси вращения. Следовательно, суммарная угловая скорость по величине и по направлению изображается диагональю параллелограмма, построенного на слагаемых угловых скоростях как на сторонах:

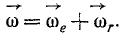
Результирующая угловая скорость эквивалентна двум слагаемым угловым скоростям, одновременно приложенным к телу. Таким образом, угловые скорости складывают как векторы и при сложении их можно менять местами:

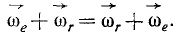
Обращаем внимание читателей, что это относится к сложению угловых скоростей, но не конечных вращений. Сложение вращений происходит не по правилам векторного исчисления, а по правилам введенного Гамильтоном исчисления кватернионов. Результат сложения двух конечных поворотов зависит от их последовательности и их нельзя менять местами.

Задача №11

Шаровая дробилка состоит из полого шара II (рис. 130, а), в котором находятся тяжелые дробящие шарики и дробимое вещество. Шар II  сидит на оси CD, на которой заклинено коническое зубчатое колесо К радиуса r. Ось CD сидит в подшипниках в раме /, составляющей одно целое с осью AB и приводящейся во вращение рукояткой с угловой скоростью ω_e. Колесо К сцеплено с неподвижным колесом L радиуса R. Определить абсолютную угловую скорость шаровой дробилки.

Решение. Рабочая камера дробилки имеет одновременно две угловые скорости: переносная направлена по оси AB и равна ω_e; относительная угловая скорость направлена по оси CD и величина ее неизвестна. Скорость зуба E подвижной шестеренки К, находящегося в данное мгновение в соприкосновении с неподвижной шестеренкой L, равна нулю, а потому мгновенная ось вращения проходит через центр О и эту точку (рис. 130, 6). Отсюда мы можем определить относительную угловую скорость:

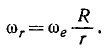
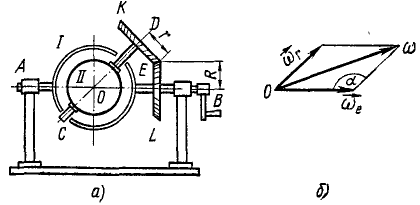
Рис. 130

Квадрат абсолютной угловой скорости определим по теореме косинусов:

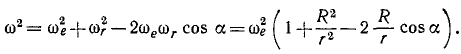
Ответ.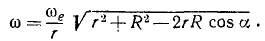 

Аналогично легко показать, что при вращении одного тела одновременно вокруг двух или нескольких параллельных осей угловые скорости надо складывать по правилам сложения параллельных векторов.

Задача №12

Найти относительную и абсолютную угловые скорости зубчатого колеса ll радиуса r (рис. 131), катящегося по неподвижному зубчатому колесу l того же радиуса н приводящегося в движение кривошипом OA, вращающимся вокруг осн неподвижного колеса с угловой скоростью ω_e; движение кривошипа OA принять за переносное.

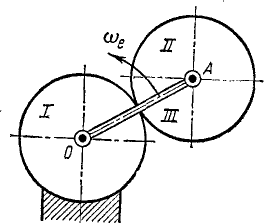
Рис. 131

Решение. Движение колеса ll будем рассматривать как составное, состоящее из двух вращательных: переносного с угловой скоростью ωe вокруг оси О против хода часов и относительного вокруг оси А, тоже против хода часов. Мгновенная ось вращения должна быть им параллельна и проходить через точку касания подвижной шестеренки ll и неподвижной шестеренки, т. е. в середине OA. Ответ получается непосредственно из закона сложения параллельных векторов.

Ответ. ω_r = ω_e; ω-2ω_e.

Задача №13

Диск с центром А (рис. 132), катящийся с угловой скоростью ω₁ = —50 ceκ^-1 внутри неподвижного диска с центром О, приводится в движение кривошипом OA, равномерно вращающимся с угловой скоростью ω₂ = 25 ceκ^-1. Определить угловую скорость диска относительно кривошипа.

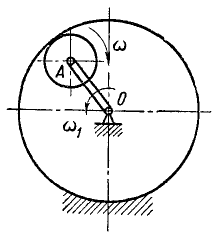
Рис. 132

Решение. Величина абсолютной угловой скорости диска ω = —50 ceκ^-1 является алгебраической суммой величин относительной угловой скорости ω_r, с которой диск вращается вокруг пальца кривошипа, и переносной угловой скорости ω_e= + 25 ceκ^-1 кривошипа. Пользуясь законами сложения векторов, направленных в противоположные стороны, имеем

ω_r = —50 ceκ^-1— 25 сек^-1 = — 75 ceκ^-l.

Ответ. ω_r = — 75 paд/ceκ.

Пара угловых скоростей сообщает телу поступательное движение.

Пара угловых скоростей

Пусть некоторое тело вращается вокруг оси AA' с угловой скоростью ω (рис. 133, а), в то время как эта ось поворачивается вокруг параллельной оси BB' с такой же угловой скоростью, но в противоположную сторону. Такую систему двух равных и противоположных векторов угловых скоростей называют парой угловых скоростей. Пара угловых скоростей сообщает всем точкам тела, к которому она приложена, одинаковые линейные скорости. Действительно, легко показать, что 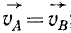, точка А имеет только вращательную скорость вокруг оси BB', равную ωAB, а точка В обладает скоростью ωAB во вращении вокруг оси AA'.

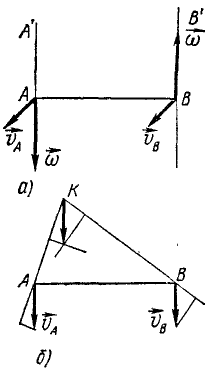
Рис. 133

Следовательно, прямая AB движется, не меняя своего направления. Чтобы установить, что движение тела поступательное, надо показать, что не меняют направления, по крайней мере, две непараллельные прямые или что три не лежащие на одной прямой точки тела всегда имеют одинаковые скорости. Третью точку К (рис. 133, б) для простоты рассуждений выберем в плоскости, в которой лежат скорости точек А и В. Согласно основной теореме кинематики твердого тела проекции скорости точки К на прямые KA и KB должны быть равны проекциям скоростей точек А и В. Отложив от точки К эти проекции и определив по проекциям скорость точки К, убедимся, что

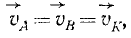    (80)

причем скорость поступательно движущегося тела равна моменту пары угловых скоростей. Вместе с тем следует иметь в виду, что причем скорость поступательно движущегося тела равна моменту пары угловых скоростей. Вместе с тем следует иметь в виду, что и поступательное движение тела можно представить в каждое мгновение парой угловых скоростей.

Задача №14

Определить абсолютную угловую скорость шестеренки III планетарного механизма, представленного на рис. 134.

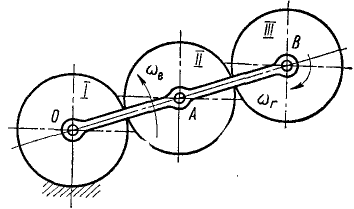
Рис. 134

Решение. Шестеренка III имеет одновременно две угловые скорости: переносную (угловую скорость кривошипа, вращающегося вокруг оси О) и относительную (вокруг оси В). Пусть кривошип вращается против хода часовой стрелки с угловой скоростью +ω_e. Чтобы определить относительное вращение, мысленно остановим переносное, будем считать кривошип неподвижным. В относительном движении шестеренка II вращается с той же угловой скоростью ωe против хода часовой стрелки, как это было показано в предыдущей задаче № 79. Колесо III в относительном движении (относительно кривошипа, принимаемого за неподвижный) вращается с такой же угловой скоростью, как и шестеренка II, но в противоположную сторону, т. е. относительная угловая скорость шестерни III:

ω_r= — ω_e.

Следовательно, к шестерне III приложена пара угловых скоростей и шестерня III совершает поступательное движение.
Ответ. ω_III = 0 („парадокс Фергюсона").

Задача №15

Чтобы отвинтить гайку с колеса автомобиля, приподнятого домкратом, шофер накинул на гайку ключ (рис. 135) и, не поворачивая ключа, вращал рукой колесо против часовой стрелки. Какое движение совершает зажатая ключом гайка?

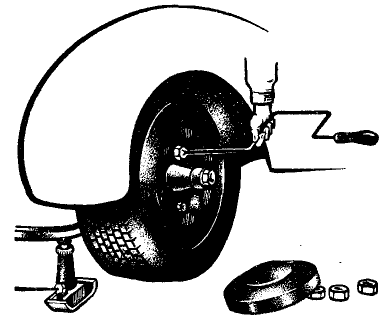
Рис. 135

Решение. Вращаясь вместе с колесом вокруг его оси против часовой стрелки, гайка одновременно поворачивается ключом вокруг оси болта по часовой стрелке. Пренебрежем пока движением гайки вдоль оси болта и рассмотрим лишь два эти вращения. Угловая скорость колеса является переносной угловой скоростью ω_e гайки, а угловая скорость гайки в ее вращении вокруг оси болта — ее относительной угловой скоростью ω_r. Нетрудно видеть, что при повороте колеса вокруг его оси на какой-либо угол φ, гайка поворачивается за то же время на такой же угол, но в другую сторону, вокруг оси болта. Следовательно

ω_е= — ω_r.

Мы имеем здесь пару угловых скоростей и гайка вместе с ключом совершает поступательное движение по окружности. Радиусы круговых траекторий, описываемых точками гайки при ее круговом поступательном движении, равны расстоянию R от оси болта до оси колеса.

Если мы примем теперь во внимание и движение гайки вдоль оси болта, то убедимся, что кроме уже рассмотренного нами кругового поступательного движения гайки имеется еще прямолинейное поступательное движение гайки в перпендикулярном направлении (вдоль оси болта). В результате сложения этих двух поступательных движений получается одно поступательное движение, при котором все точки гайки описывают одинаковые и одинаково расположенные винтовые линии радиуса R с шагом, равным шагу нарезки болта. Это же движение гайки можно рассматривать как состоящее из переносного вращательного вокруг оси колеса и относительного винтового вокруг оси болта.