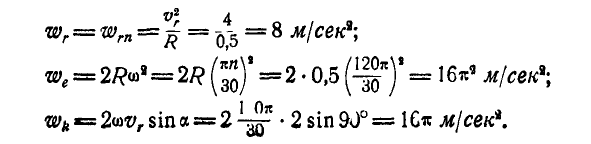Сложение движений точки в теоретической механике

Сложение движений точки:

Рассмотрим сложение движений точки, т. е. такие случаи, когда точка участвует в нескольких движениях одновременно.

Примерами сложения движений могут служить движение пассажира по движущемуся пароходу, движение ползуна в механизме по подвижной направляющей и пр.

При изучении сложения движений точки М введем в рассмотрение основную (иначе говоря, абсолютную или неподвижную) систему отсчета в виде неподвижных координатных осей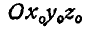

Пусть теперь тело А (неизменяемая среда), с которой скреплены и вместе с ней движутся оси координат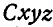

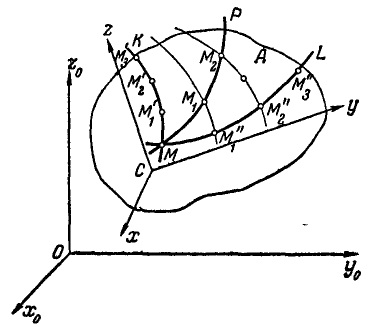
Рис.211.

Допустим, далее, что в среде, в свою очередь, движется точка М, которая участвует в двух движениях — относительном по отношению к среде (или по отношению к осям координат 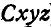) и в переносном вместе со средой, т. е. вместе с осями .

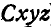Относительным движением точки М называется движение ее по отношению к подвижной системе отсчета 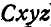(к среде).

Для исследования относительного движения точки М следует подвижные оси 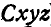закрепить неподвижно и при этом условии рассмотреть движение точки М по неподвижной теперь среде.

Переносным движением точки М называется движение ее, происходящее вместе с движением подвижной системы отсчета 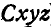(среды) по отношению" к неподвижной системе отсчета .

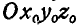Для исследования переносного движения точки М точку следует скрепить с движущейся средой и рассмотреть движение ее по отношению к неподвижным осям .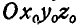

Абсолютным движением точки М называется движение ее относительно основной системы отсчета, т. е. неподвижных осей .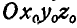

Абсолютное движение точки М получается в результате сложения движений относительного и переносного. В самом деле, пусть за промежутки времени 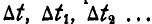точка М (рис. 211), двигаясь по относительной траектории К, занимает на ней ряд последовательных положений 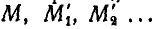; но за эти промежутки времени ее относительная траектория, двигаясь вместе со средой, будет занимать ряд последовательных положений 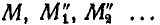на переносной траектории L. Абсолютная траектория точки М пройдет через точки 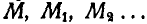, которые получим, если на относительной траектории отложить дуги

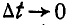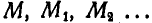При точки образуют плавную кривую.

Таким образом, абсолютное движение точки является составным из относительного и переносного движений.

Докажем теперь следующую теорему:

Скорость абсолютного движения точки равна геометрической сумме скоростей переносного и относительного движений.

Пусть имеются неподвижная система отсчета 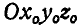и подвижная система 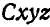, связанная со средой. Тогда положение точки М, движущейся по отношению к среде, определяется по отношению к неподвижной системе радиусом-вектором 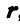, а по отношению к подвижной системе — радиусом-вектором 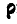; положение точки С среды по отношению к неподвижным осям определяется радиусом-вектором 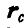(рис. 212).

Из чертежа имеем: 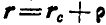, но так как:

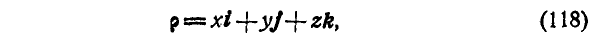
то можно написать:

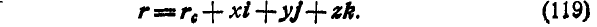
На основании равенств (72) и (119) найдем, что скорость абсолютного движения точки М:

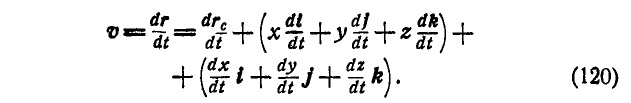
Первое слагаемое равенства (120) представляет собой скорость точки С. Второе слагаемое — это производная по времени от 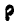 в предположении, что координаты х, у и z точки М постоянные. Поэтому второе слагаемое есть скорость точки М среды по отношению к точке С.

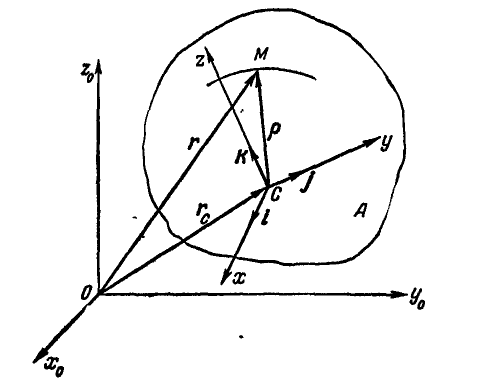
Рис. 212.

Следовательно, первые два слагаемых представляют скорость переносного движения 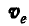точки среды, совпадающей с точкой М.

Третье слагаемое — производная от 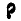в предположении, что i, j и k постоянные величины. Это скорость относительного движения  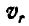точки М по отношению к осям Cxyz. Поэтому окончательно имеем:

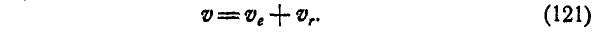
Задача №1

Мотовило состоит из шести планок, расположенных на поверхности цилиндра радиусом R на равном расстоянии одна от другой (рис. 213). Планки, связанные в одно целое, вращаются равномерно с угловой скоростью 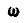вокруг геометрической оси О цилиндра, которая, в свою очередь, перемещается с постоянной горизонтальной скоростью 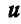. Найти проекции абсолютной скорост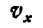и и 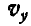на координатные оси и уравнения абсолютного движения центра какой-либо планки А.

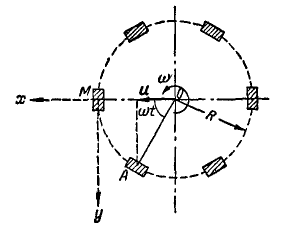
Рис. 213.

Решение. Каждая планка мотовила участвует в двух движениях — относительном вращении вокруг оси О и в переносном движении вместе с осью О. Относительная траектория любой планки — окружность радиуса R. Проведя координатные оси х и у через точку М, расположенную на левом конце горизонтального диаметра, найдем уравнения относительного движения центра планки А:

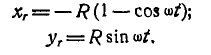
Отсюда находим проекции относительной скорости точки А на координатные оси:

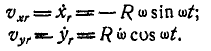
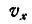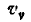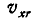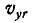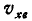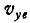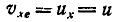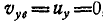Для нахождения проекций и абсолютной скорости точки А на координатные оси следует в проекциям скорости и относительного движения точки прибавить проекции скорости и переносного ее движения. Но так как и , то:

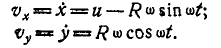
Отсюда уравнения абсолютного движения планки определятся:

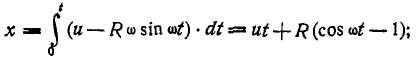
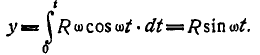
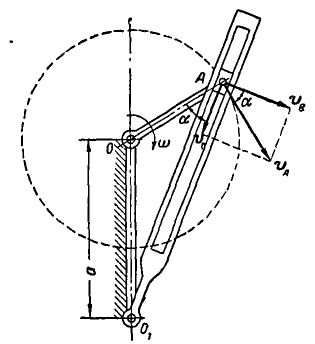
Рис. 214.

Задача №2

Механизм (рис. 214) состоит из кривошипа ОА и качающейся кулисы 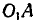, могущих вращаться вокруг параллельных валов О и .

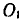Конец А кривошипа соединен с ползуном, скользящим вдоль прореза кулисы. Зная, что кривошип вращается с постоянной угловой скоростью 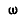и что длины 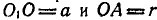, определить:

1) угловую скорость 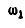 вала 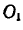, в зависимости от расстояния  ;

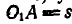2) наибольшее и наименьшее значение угловой скорости ;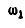

3) те положения кривошипа, когда .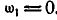

Решение. Для нахождения 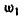, исследуем движение точки А. С одной стороны, это движение можно рассматривать как движение, происходящее по окружности с абсолютной скоростью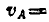 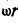. С другой стороны, точка А участвует в двух движениях — переносном вместе с кулисой, имея переносную скорость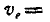 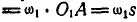 , и в относительном вдоль прорези со скоростью .

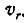Далее, 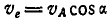, или 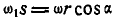, отсюда:

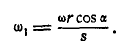
Из 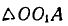находим 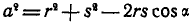, откуда:

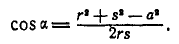
Следовательно:

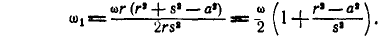
Угловая скорость 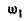  будет иметь наибольшее значение при 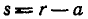, а наименьшее при 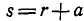; поэтому:

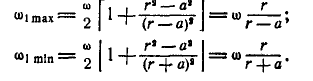
Из общего выражения для 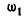, находим, что

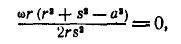
а для этого необходимо, чтобы 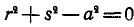, или , но это будет, когда .

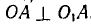При нахождении абсолютного ускорения точки, участвующей в двух движениях, различают два случая:

1)    когда среда (или подвижная система отсчета) совершает поступательное движение,

2)    когда среда совершает вращательное движение.

Рассмотрим сначала первый случай.

Здесь оси 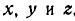, связанные со средой (рис. 212), движутся параллельно самим себе и поэтому единичные векторы этих осей 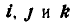не изменяют своего направления. Следовательно, на основании равенств (79) и (119) абсолютное ускорение точки М будет:

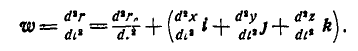
Первое слагаемое правой части последнего равенства представляет собой ускорение точки С  среды, т. е. переносное ускорение 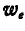; второе слагаемое, стоящее в скобках, — ускорение точки М по отношению к осям 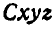, т. е. относительное ускорение 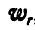, следовательно:

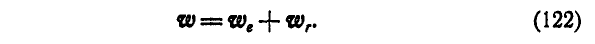
Отсюда следует, что при поступательном движении среды абсолютное ускорение точки равно геометрической сумме ускорений переносною и относительного движений.

Найдем теперь абсолютное ускорение точки М в том случае, когда среда совершает вращательное движение. В этом случае на основании равенств (79) и (120) получим абсолютное ускорение точки М (рис. 212):

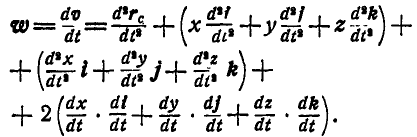
В правой части последнего равенства первое слагаемое представляет собой ускорение точки С среды.

Второе слагаемое является второй производной от 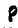, определяемого равенством (118) в предположении, что координаты точки М по отношению к осям 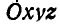постоянны. Следовательно, второе слагаемое — это ускорение точки среды, совпадающей с точкой М, по отношению к точке С.

Поэтому первое и второе слагаемое вместе дают ускорение точки среды, совпадающей с точкой М, т. е. ускорение переносного движения .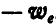

Третье слагаемое представляет собой вторую производную от 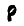в предположении, что единичные векторы 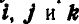не изменяют своего направления, что характеризует движение точки М по отношению к среде. Следовательно, третье слагаемое есть относительное ускорение точки по отношению к среде — .

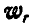Преобразуем несколько четвертое слагаемое. На основании равенства (100) сможем написать:

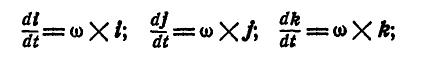
отсюда:

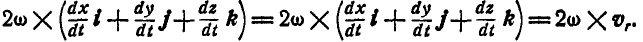
Обозначая

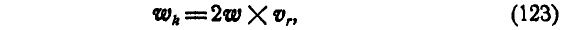
будем иметь:

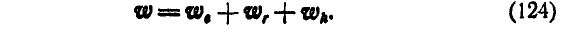
Итак, в общем случае абсолютное ускорение точки равно геометрической сумме трех ускорений — переносного, относительного и поворотного.

В этом заключается теорема Кориолиса. Ускорение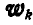, определяемое равенством (123), называется поворотным, добавочным или кориолисовым ускорением. Его модуль определяется по формуле:

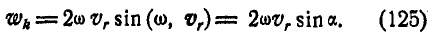
Из равенства (125) следует, что поворотное ускорение обращается в нуль в двух случаях:

1)    когда 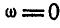, т. е. среда движется поступательно, и    

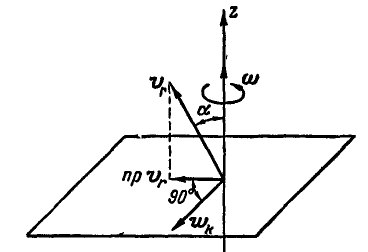
Рис. 215.

2)    когда 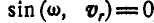, т. е. если относительная скорость  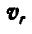точки М параллельна оси вращения среды.

Направление ускорения 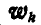определяется по общему правилу векторного произведения. Для этого на основании равенства (123) следует вектор относительной скорости точки 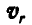(рис. 216) спроектировать на плоскость, перпендикулярную к оси вращения среды, или, что то же, — к вектору 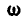, и полученную проекцию относительной скорости повернуть на 90° в сторону вращения среды.

Задача №3

Тележка скатывается вниз по наклонной плоскости; ее движение в метрах и секундах выражается уравнением 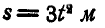 (рис. 216, а).

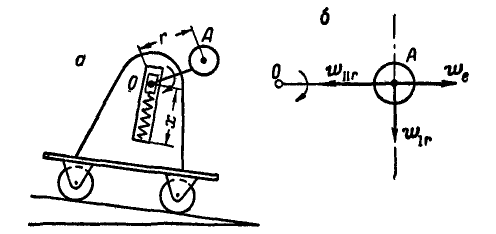
Рис. 216.

На тележке имеется ползун О, совершающий гармоническое колебательное движение в направлении, перпендикулярном наклонной плоскости, по закону 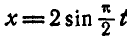 . С ползуном в точке О скреплен шарнирно стержень ОА, на конце которого насажен груз А, вращающийся вместе со стержнем вокруг точки О с угловой скоростью, соответствующей .

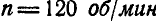Найти абсолютное ускорение 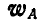 груза в момент 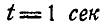, когда точка А расположена в крайнем правом положении, а стержень OA параллелен наклонной плоскости. Величина ОА = г= 0,2 м.

Решение. Груз участвует в трех движениях: в переносном— вместе с тележкой, в относительном поступательном — вместе с ползуном О по отношению к тележке и в относительном вращательном — по отношению к оси .

Обозначим ускорения, соответствующие этим движениям груза А, через 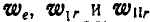 ;  тогда абсолютное его ускорение найдется по формуле (122):

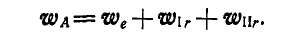
Величина каждого из этих ускорений определится:

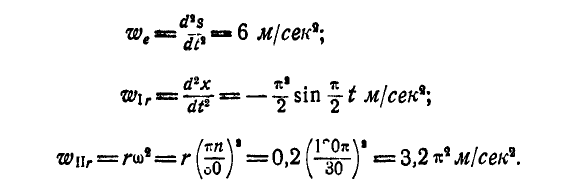
При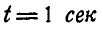

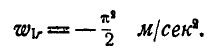
Построение векторов 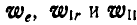показано на рисунке 216,6. Величина абсолютного ускорения точки будет:

Задача №4

Движение центра цилиндра радиусом 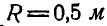в метрах и секундах выражается уравнением: 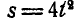. Через цилиндр перекинута нить, к концам которой прикреплены два груза А и В (рис. 217). Предполагая, что при движении цилиндра нить сматывается с цилиндра и наматывается на него без скольжения, определить абсолютные ускорения 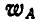и 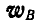грузов А и В.

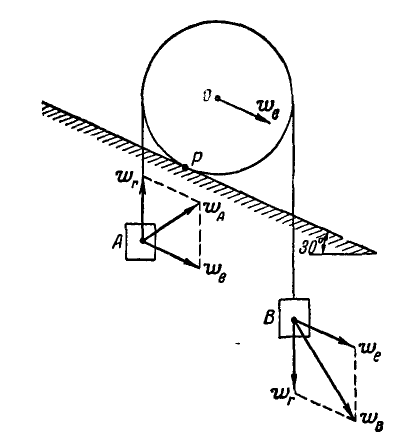
Рис. 217.

При решении задачи считать, что грузы раскачиваться не могут.

Решение. Каждый из грузов участвует в двух движениях: в переносном с ускорением 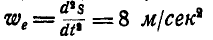 и в относительном по отношению к центру цилиндра с ускорением  .

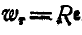Угловая скорость мгновенного вращения цилиндра:

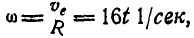
откуда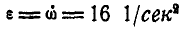

и, следовательно:

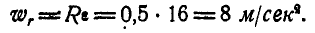
Абсолютные ускорения 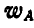и 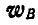грузов А и В найдутся по правилу параллелограмма:

• Заказать решение задач по теоретической механике

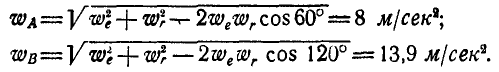
Задача №5

По окружности диска радиусом 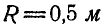в противоположную сторону его вращения движется точка М с постоянной относительной скоростью 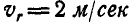(рис. 218).

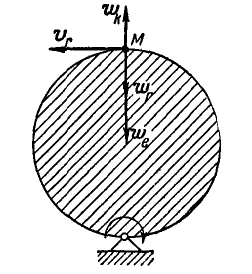
Рис. 218.

Диск вращается вокруг оси, проходящей через точку О перпедикулярно плоскости чертежа в направлении, указанном стрелкокй, делая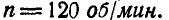 

Найти полное ускорение 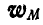 точки М.

Решение. Так как среда (диск) вращается вокруг неподвижной оси, то абсолютное ускорение точки М равно геометрической сумме трех ускорений (124), из которых:

Исходя из направления ускорений (рис. 218), находим:

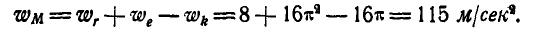
Задача №6

Полое кольцо радиуса вращается с постоянной угловой скоростью 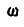вокруг оси, проходящей через точку О, перпендикулярно к плоскости чертежа. Кольцо заполнено жидкостью, движущейся в нем против стрелки часов с относительной скоростью 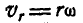(рис. 219).

Определить величины и направления абсолютных ускорений частиц жидкости, расположенных в точках 1, 2, 3 и 4.

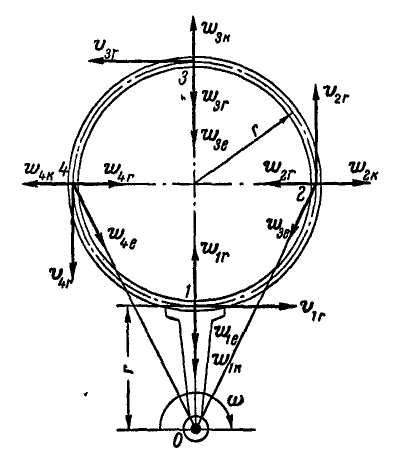
Рис. 219.

Решение. Так как движение среды (кольца) вращательное, то абсолютное ускорение частицы жидкости в любом положении 1, 2, 3 и 4 будет равно: .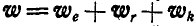

Векторы ускорений 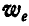, 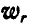и для частиц жидкости в каждом положении 1, 2, 3 и 4 построены на рисунке 219.

Величины составляющих абсолютного ускорения частиц жидкости в положениях 1, 2, 3 и 4 будут:

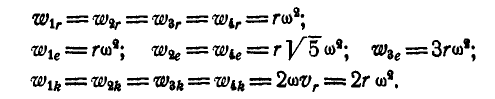
Нетрудно видеть, что абсолютные ускорения в точках 1, 2, 3 и 4 направлены в рассматриваемом положении кольца по вертикали вниз и равны по величине:

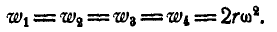
Задача №7

На рисунке 220 изображена лопатка центробежного водяного насоса, имеющая очертание дуги окружности с центром в точке В, расположенной на одной горизонтали с осью вращения насоса О.

Определить абсолютное ускорение частицы А воды, движущейся по лопатке с относительной скоростью 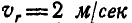и относительным тангенциальным ускорением 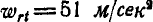. Угловая скорость насоса 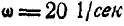и .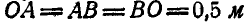

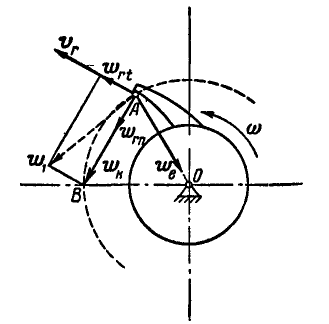
Рис. 220.

Решение. Лопатка насоса совершает вращательное движение, поэтому абсолютное ускорение частицы А равно геометрической сумме трех ускорений:

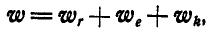
причем

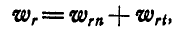
где по условию:

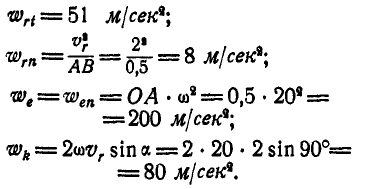
Векторы всех составляющих абсолютного ускорения частицы показаны на рисунке 220. Заменим сначала ускорения 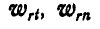и 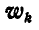одним ускорением 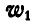, величина которого:

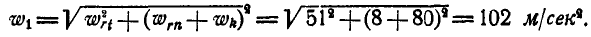
Так как величина 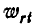в два раза меньше 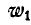, то угол между векторам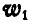и и 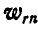, или, что то же, между 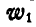и 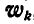, равен 30°. Отсюда заключаем, что угол между векторам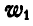и и 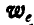равен 90°.

Поэтому величина абсолютного ускорения точки А:

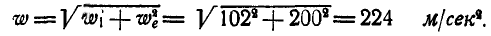
Задача №8

При изменении угловой скорости маховика стержень регулятора 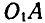поворачивается вокруг оси 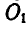. Маховик, вращающийся с угловой скоростью 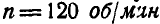, получает мгновенное угловое ускорение 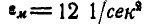. При этом стержень 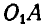имеет угловое ускорение 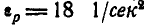и относительная скорость точки А равна  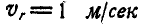(рис. 221). Определить абсолютное ускорение точки А центра груза регулятора в момент, когда оси вращения 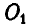и О регулятора и маховика расположены на одной вертикали, есл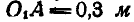и и .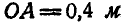

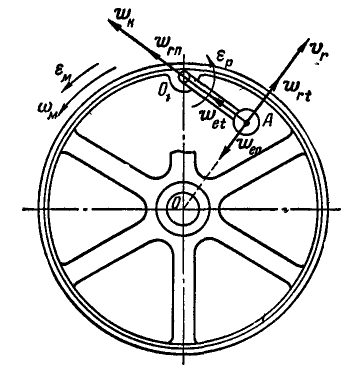
Рис. 221.

Решение. Движение среды (маховика) вращательное, а поэтому абсолютное ускорение точки А:

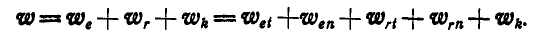
Величины составляющих абсолютного ускорения точки А при 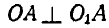будут: 

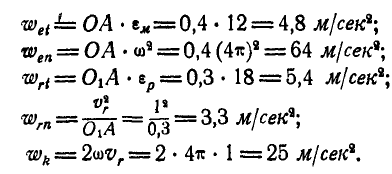
Векторы всех вычисленных составляющих абсолютного ускорения точки А построены на рисунке 221.

Из чертежа находим, что величина абсолютного ускорения точки А составляет:

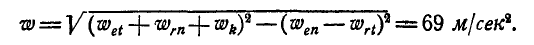
Задача №9

Для очистки картофеля от почвы во время его уборки вся масса вместе с почвой поступает в чашевую центрифугу; последняя имеет форму усеченного конуса и вращается вокруг вертикальной оси с угловой скоростью .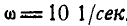

Боковая поверхность центрифуги состоит из стальных прутьев, совпадающих с образующими конуса, вдоль которых перемещаются клубни картофеля (рис. 222).

Рассматривая клубень А как материальную точку и зная, что движение его в метрах и секундах выражается уравнением 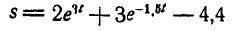, определить полное ускорение клубня в момент 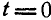, если известно, что образующая конуса составляет с его осью угол . 

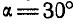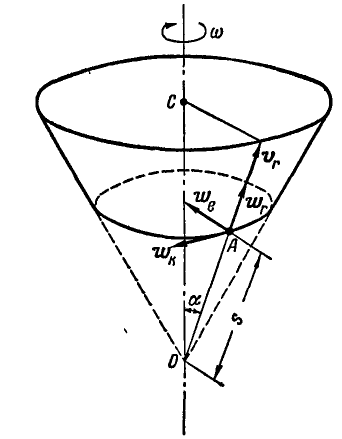
Рис. 222.

Решение. Так как прямая ОА, вдоль которой движется клубень, вращается вокруг оси ОС, то полное ускорение точки А равно геометрической сумме трех ускорений: относительного, переносного и поворотного. Относительное ускорение: 

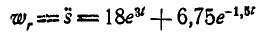, так как .

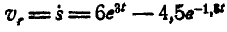Переносное ускорение:

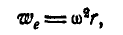
где 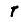—расстояние точки А от оси вращения. К моменту t это расстояние будет:

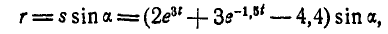
откуда:

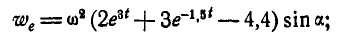
направлено это ускорение от А к оси конуса. Поворотное ускорение:

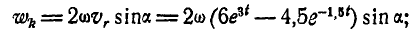
оно направлено перпендикулярно к в сторону вращения конуса. При ; ; 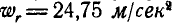; 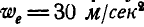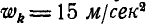. Заменим сначала векторы 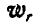и 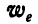одним результирующим вектором 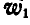. По теореме косинусов найдем:

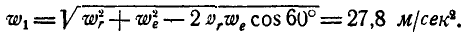
Так как векторы 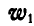и 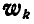взаимно перпендикулярны, то полное ускорение точки А будет:

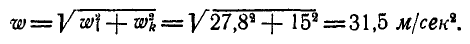
Задача №10

Механизм качающейся паровой машины (рис. 223) состоит из кривошипа OA, вращающегося вокруг точки О с постоянной угловой скоростью 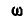, и стержня AD, соединенного шарнирно с кривошипом и скользящего внутри муфты В, могущей вращаться. Определить скорость и ускорение точки прямой AD, совпадающей с точкой В, а также радиус кривизны траектории этой точки.

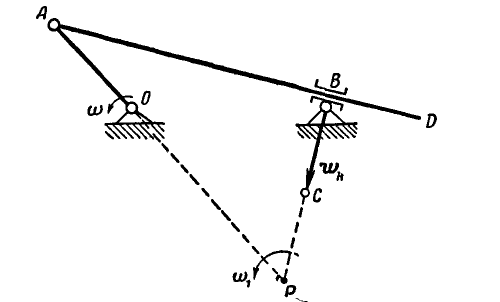
Рис. 223.

Решение. Плоскость, вращающаяся вокруг В. является подвижной системой (средой), а прямая AD —относительной траекторией точки В.

Так как точка среды, совпадающая с В, находятся в покое, то 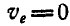, поэтому абсолютная и относительная скорости точки В совпадают: .

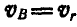Переносное ускорение точки В равно нулю, поэтому по формуле (124) имеем:  .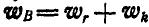

Проектируя это равенство на направление BP, замечаем, что .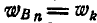

Но так как

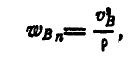
то

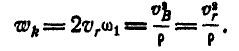
Отсюда находим радиус кривизны 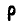траектории точки В:

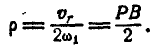
Следовательно, центр кривизны С делит пополам отрезок BP.