Сложение движение твердого тела в теоретической механике

Содержание:

Сложение движение твердого тела:

В простейшем случае рассматривают сложение двух движений твердого тела, одно из которых является переносным, другое — относительным. Относительным движением твердого тела считают его движение, в простейшем случае поступательное или вращательное, относительно подвижной системы осей координат, движущейся относительно другой, основной или неподвижной, системы координат, т. е. системы координат, движение которой относительно других систем координат не рассматривается.

Переносным движением твердого тела называют его движение, тоже в простейшем случае поступательное или вращательное, вместе с подвижной системой координат в рассматриваемый момент времени относительно неподвижной. Сложным движением твердого тела называется его движение относительно основной или неподвижной системы координат. Составление сложного движения из переносного и относительного в простейшем случае или нескольких переносных и относительных движений в общем случае, называют сложением движений твердого тела. Обратный процесс называется разложением движения твердого тела на составляющие движения. Этот процесс всегда возможен и для него справедливы формулы, полученные для сложения движений твердого тела.

Плоское и движение свободного твердого тела считают уже сложными. В общем случае переносное и относительное движения твердого тела могут быть любыми сложными движениями тела.

При рассмотрении сложного движения твердого тела, состоящего из нескольких движений, рассматривают сложение его движений не за конечный промежуток времени, а в рассматриваемый момент времени, т. е. в действительности рассматривается сложение скоростей линейных и угловых. Для вычисления ускорений точек тела следует использовать формулу для сложного движения точки или формулы для ускорений точек того движения твердого тела, которое получается в результате сложения движений.

Сложение поступательных движений твердого тела

Имеем твердое тело, участвующее одновременно в двух поступательных движениях, одно из которых является переносным со скоростью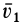

Установим вид сложного движения. Для этого вычислим скорость какой-либо точки 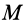тела относительно неподвижной системы координат 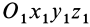. По теореме сложения скоростей для точки имеем

так как переносное и относительное движения тела являются поступательными. Это справедливо для любой точки рассматриваемого тела, а потому сложное движение тела является поступательным со скоростью 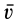. Таким образом, от сложения двух поступательных движений твердого тела получается поступательное движение со скоростью, равной векторной сумме скоростей составляющих поступательных движений.

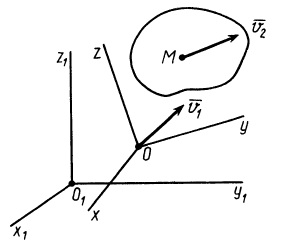
Рис. 94

Если имеется последовательность поступательных движений тела, первое из которых является относительным по отношению к переносному второму, а это второе — относительным к переносному третьему и т. д. (скорости таких последовательных движений соответственно 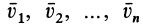), то от сложения этих движений путем последовательного применения (1) получим поступательное движение тела со скоростью

Сложение вращательных движений твердого тела

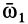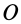1. Сложение вращений вокруг пересекающихся осей. Пусть твердое тело участвует одновременно в двух вращениях: переносном с угловой скоростью  и относительном с угловой скоростью . Оси вращений пересекаются в точке (рис. 95,а). Векторы угловых скоростей как скользящие векторы можно считать перенесенными в точку 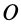осей вращения.

Примером тела, участвующего в двух вращениях вокруг пересекающихся осей, является диск 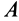, свободно насаженный на ось 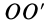и вращающийся вокруг нее с угловой скоростью  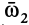. Вместе с осью 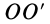диск еще вращается вокруг другой оси  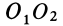(рис. 95,6) с угловой скоростью .

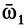Определим вид движения твердого тела, участвующего в двух вращениях вокруг пересекающихся осей. Точка 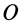тела, расположенная на пересечении осей вращения, является неподвижной, и ее абсолютная скорость 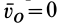. Докажем, что любая другая точка 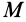тела, находящаяся на диагонали параллелограмма, построенного на векторах угловых скоросте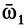й и , тоже имеет в рассматриваемый момент скорость, равную нулю.

По теореме о сложении скоростей для точки имеем

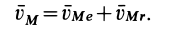
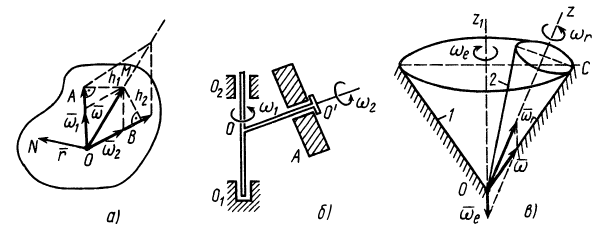
Рис. 95

Так как переносное и относительное движения являются вращениями вокруг осей, то

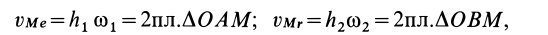
где 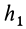и 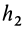— кратчайшие расстояния от точки 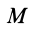до соответствующих осей вращения. Площади треугольников в параллелограмме равны, поэтому 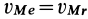. Векторы скоросте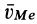й и 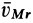имеют противоположные направления. Таким образом, 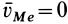. Это справедливо для любой точки 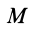, расположенной на диагонали параллелограмма, так как масштаб векторов можно изменять. Точки оси 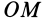имеют скорости, равные нулю. Следовательно,  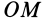является мгновенной осью вращения тела в рассматриваемый момент, т. е. при сложении двух вращений вокруг пересекающихся осей, одно из которых переносное, а другое — относительное, получается вращение тела вокруг мгновенной оси.

Для определения абсолютной угловой скорости вращения вокруг мгновенной оси выберем на теле точку 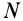и вычислим ее скорость один раз как скорость сложного движения, а другой — как вращения вокруг мгновенной оси. По формуле Эйлера для вращательных движений при сложном движении имеем

Для абсолютного вращения вокруг мгновенной оси

vN = (bx F.

Приравнивая скорости, получаем

т. е. угловая скорость абсолютного вращения равна векторной сумме угловых скоростей составляющих вращений.

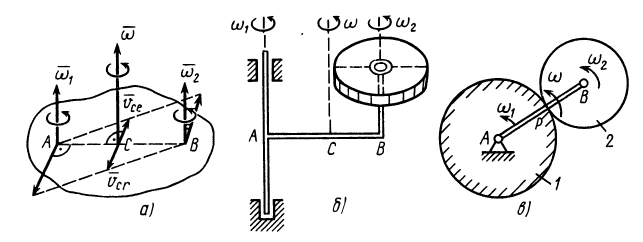
Рис. 96

Последовательное применение этого правила сложения вращений вокруг пересекающихся осей позволяет заменить любое количество вращений вокруг пересекающихся осей одним вращением, угловая скорость которого равна векторной сумме угловых скоростей составляющих вращений, т. е.

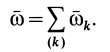
Тело, участвующее в двух вращениях вокруг пересекающихся осей, имеет неподвижную точку, расположенную на пересечении осей. Оно вращается вокруг неподвижной точки, т. е. совершает сферическое движение. Таким образом, сферическое движение твердого тела можно считать состоящим из двух вращений вокруг пересекающихся осей: переносного и относительного.

Сферическое движение совершает конус 2 при качении без скольжения по неподвижному конусу 1 (рис. 95, в). Его движение можно считать двумя вращениями вокруг пересекающихся осей. Относительное вращение происходит вокруг оси подвижного конуса 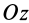с угловой скоростью 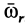, а переносное — вокруг оси неподвижного конуса 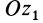с угловой скоростью 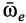. Абсолютным движением является вращение вокруг мгновенной оси 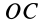с угловой скоростью

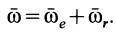
Мгновенная ось 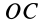, как и ось подвижного конуса 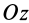, вращается вокруг оси неподвижного конуса 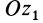с угловой скоростью .

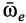От движения подвижного конуса по неподвижному без скольжения легко перейти к движению подвижной конической шестерни по неподвижной шестерне, если у конусов отрезать их части плоскостями, перпендикулярными осям 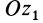и .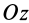

2. Сложение вращений вокруг параллельных осей. Следует рассмотреть три случая.

1) Вращения имеют одинаковые направления. Тело участвует в двух вращениях: переносном с угловой скоростью 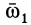и относительном с угловой скоростью 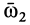(рис. 96, а). Таким телом является диск, представленный на рис. 96, б. Пересечем оси вращения перпендикулярной прямой. Получим точки пересечения 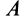и 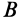, в которые можно перенести векторы угловых скоросте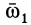й и 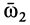. На отрезке 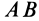тела в рассматриваемый момент имеется точка , скорость которой равна нулю. Действительно, по теореме сложения скоростей для точки , имеем

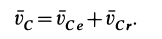
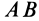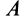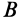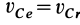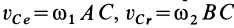Точки тела, для которых переносная и относительная скорости параллельны и противоположны, могут находиться только на отрезке между точками и . Скорость точки равна нулю, если . Но . Следовательно,

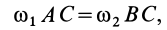
или

Прямую, перпендикулярную осям вращения, можно провести на любом расстоянии. Следовательно, существует ось, скрепленная с телом и параллельная осям вращения, скорости точек которой равны нулю в данный момент. Она является мгновенной осью вращения в рассматриваемый момент времени.

Для определения угловой скорости 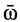вращения тела вокруг мгновенной оси вычислим скорость точки 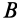, считая ее движение сложным. Получим

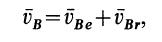
но

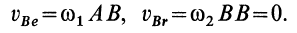
Следовательно,

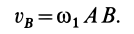
Для скорости точки 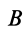при вращении тела вокруг мгновенной оси имеем

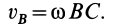
Приравнивая скорости точки 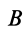, полученные двумя способами, имеем

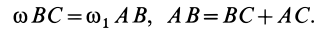
Согласно (4),

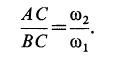
Поэтому

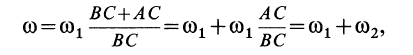
т. е.

Формулу (4) можно представить в следующем виде:

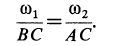
Образуя производную пропорцию и используя формулу (5), получим

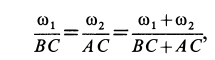
или

Таким образом, при сложении двух вращений тела вокруг параллельных осей в одинаковых направлениях получается вращение вокруг параллельной оси в том же направлении с угловой скоростью, равной сумме угловых скоростей составляющих вращений. Мгновенная ось полученного вращения делит отрезок между осями составляющих вращений на части, обратно пропорциональные угловым скоростям этих вращений, внутренним образом. Точка 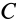при таком делении располагается между точкам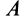и и .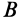

Естественно, справедливо и обратное. Вращение вокруг оси с угловой скоростью 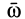можно разложить на два вращения вокруг двух параллельных осей с угловыми скоростям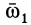и и .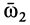

Тело, участвующее в двух вращениях вокруг параллельных осей, совершает плоское движение. Плоское движение твердого тела можно представить как два вращения, переносное и относительное, вокруг параллельных осей. Плоское движение колеса сателлита 2 по неподвижному колесу 1 (рис. 96, в) является примером движения, которое можно заменить двумя вращениями вокруг параллельных осей в одном и том же направлении, например против движения часовой стрелки. Колесо сателлита совершает переносное вращение вместе с кривошипом 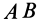вокруг оси, проходящей через точку 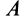с угловой скоростью 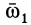, и относительное вращение вокруг оси, проходящей через точку 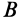с угловой скоростью 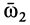. Оба вращения имеют одинаковые направления. Абсолютное вращение происходит вокруг оси, проходящей через точку 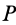, которая является в данный момент 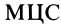. Она находится в месте соприкосновения колес, если подвижное колесо катится без скольжения по неподвижному. Угловая скорость абсолютного вращения

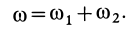
Абсолютное вращение с этой угловой скоростью происходит в том же направлении, что и составляющие движения.

2) Вращения имеют противоположные направления. Рассмотрим случай, когда 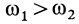(рис. 97, а). Получим следующие формулы:

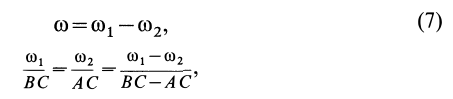
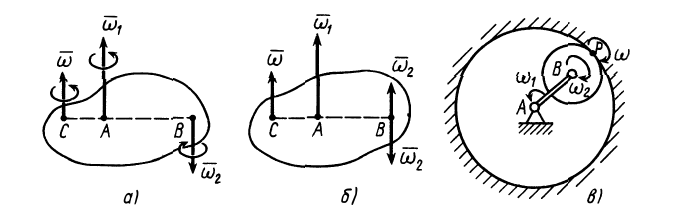
Рис. 97

или

Для вывода этих формул разложим вращение с угловой скоростью  на два вращения в том же направлении вокруг двух параллельных осей с угловыми скоростями и . Ось одного из вращений с угловой скоростью 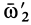возьмем проходящей через точку 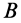и выберем 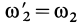. Другое вращение с угловой скоростью со пройдет через точку 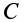(рис. 97, б). На основании (5) и (6) имеем

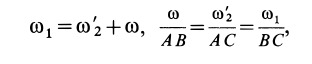
или

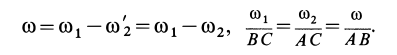
Справедливость формул (7) и (8) доказана. Таким образом, при сложении двух вращений твердого тела вокруг параллельных осей в противоположных направлениях получается вращение вокруг параллельной оси с угловой скоростью, равной разности угловых скоростей составляющих вращений в сторону вращения с большей угловой скоростью. Ось абсолютного вращения делит отрезок между осями составляющих вращений на части, обратно пропорциональные угловым скоростям этих вращений внутренним образом. Точка при таком делении находится на отрезке за точкой 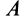, через которую проходит ось вращения с большей угловой скоростью.

Можно также одно вращение разложить на два вокруг параллельных осей с противоположными направлениями вращения. Примером плоского движения твердого тела, которое может быть представлено двумя вращениями вокруг параллельных осей в противоположных направлениях, является движение колеса сателлита, катящегося внутри неподвижного колеса без скольжения (рис. 97, в). Переносным в этом случае является вращение колеса 2 вместе с кривошипом 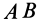 с угловой скоростью 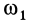вокруг оси, проходящей через точку 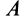. Относительным будет вращение колеса 2 вокруг оси, проходящей через точку 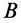с угловой скоростью 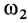, и абсолютным — вращение этого колеса вокруг оси, проходящей через 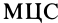, точку 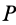, с угловой скоростью 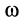. В этом случае 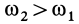и потому угловая скорость абсолютного вращения 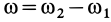. Это вращение по направлению совпадает с направлением вращения, имеющим большую угловую скорость. Ось абсолютного вращения расположена вне отрезка 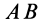за осью вращения с большей угловой скоростью.

3. Пара вращений. Парой вращений называется совокупность двух вращений твердого тела, переносного и относительного, вокруг параллельных осей с одинаковыми угловыми скоростями в противоположных направлениях (рис. 98, а). В этом случае . Рассматривая движение тела как сложное, по теореме сложения скоростей для точки имеем

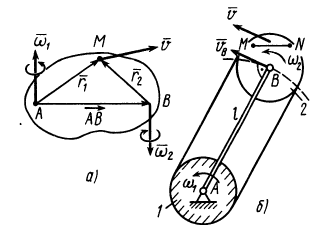
Рис. 98

Составляющие движения являются вращениями с угловыми скоростям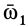и и 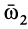. По формуле Эйлера для них получим

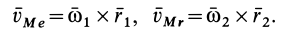
После этого для абсолютной скорости имеем

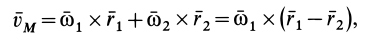
так как 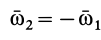. Учитывая, что 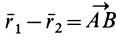, получаем

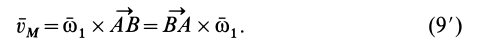
Так как векторное произведение 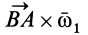 можно назвать моментом угловой скорости  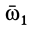относительно точки 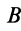, то

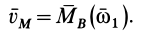
Заменяя в формуле (9') 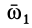на 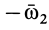, соответственно получим

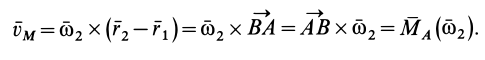
Объединяя результаты, имеем

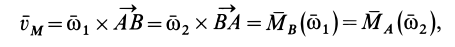
или

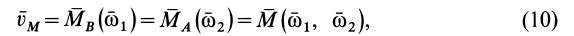
где 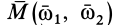является векторным моментом пары вращений .

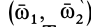Таким образом, если твердое тело участвует в паре вращений, то скорости всех точек тела, согласно (10), одинаковы, т. е. тело совершает при этом мгновенное поступательное движение. При длительном участии тела в паре вращений будет длительным и поступательное движение. Скорость поступательного движения тела

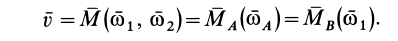
Она равна векторному моменту пары вращений, который может быть также выражен векторным моментом одной из угловых скоростей относительно какой-либо точки, расположенной на оси вращения тела с другой угловой скоростью, входящей в пару вращений. Скорость поступательного движения тела, участвующего в паре вращений, зависит только от характеристик пары вращений. Она перпендикулярна осям пары вращений. Числовое ее значение можно выразить как

где 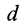—кратчайшее расстояние между осями пары или плечо пары.

Пара вращений аналогична паре сил, действующей на твердое тело. Угловые скорости вращения тела, аналогично силам, являются векторами скользящими. Векторный момент пары сил является вектором свободным. Аналогичным свойством обладает и векторный момент пары вращений.

Пару вращений и ее эквивалентность поступательному движению можно наглядно продемонстрировать на приборе (рис. 98,6), состоящем из неподвижной 1 и подвижной 2 шестеренок, соединенных цепью. При вращении кривошипа вокруг оси, проходящей через точку , шестеренка 2 будет участвовать в двух вращениях вокруг параллельных осей: переносном вместе с кривошипом и относительном вокруг оси, проходящей через точку . Вращения противоположны. Их угловые скорости одинаковы. Скорости всех точек шестеренки 2 равны скорости точки , причем 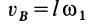все время при движении этой шестеренки.

Если с шестеренкой 2 скрепить прямолинейный отрезок 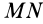, то он при движении механизма будет оставаться параллельным своему первоначальному положению. Если этот горизонтальный отрезок совместить с дном стаканчика с водой, прикрепив стаканчик к подвижной шестеренке, то вода не выльется из стаканчика при движении механизма в вертикальной плоскости.

При поступательном движении траектории всех точек тела одинаковы. Точка 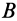описывает окружность радиуса  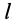. Траектории всех других точек подвижной шестеренки будут тоже окружностями такого же радиуса. Тело, участвующее в паре вращений, совершает плоское поступательное движение.

• Заказать решение задач по теоретической механике

Сложение поступательного и вращательного движений

Если тело одновременно участвует в переносном поступательном движении со скоростью 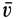и относительном вращательном с угловой скоростью 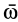, то в зависимости от их взаимного расположения целесообразно рассмотреть три отдельных случая.

1. Скорость поступательного движения перпендикулярна оси относительного вращения. В этом случае векторы 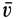и 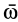перпендикулярны (рис. 99). На линии 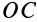, перпендикулярной плоскости,  в которой расположены 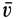и 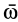, имеется точка 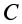, скорость которой равна нулю.

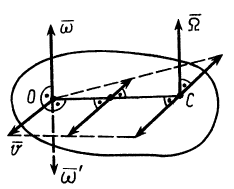
Рис. 99    

Определим ее расстояние от точки 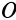. По теореме сложения скоростей для точки 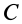имеем

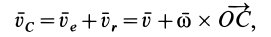
так как при вращении вокруг оси

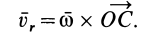
Учитывая, что скорост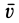и и 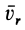противоположны по направлению, получим

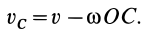
Так как 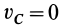, то 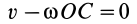и, следовательно, точк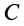и и 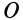находятся на расстоянии

Другие точки, имеющие скорости, равные нулю, располагаются на линии, проходящей через точку 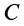, параллельно оси вращения тела с угловой скоростью 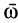. Таким образом, имеется мгновенная ось вращения, параллельная оси относительного вращения и проходящая через точку 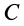. Для определения угловой скорости абсолютного вращения 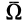вычислим скорость, например, точки 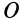двумя способами. Считая движение сложным, имеем

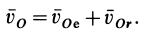
Точка 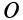находится на оси относительного вращения, и поэтому 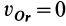. Скорость переносного движения 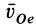в рассматриваемом случае переносного поступательного движения равна 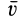. Следовательно, 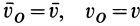. С другой стороны, эквивалентное абсолютное движение тела является вращением вокруг мгновенной оси, проходящей через точку 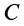с угловой скоростью 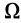. Поэтому для скорости точки 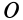имеем

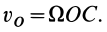
Приравнивая скорости точки 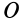, вычисленные двумя способами и используя (12), получаем

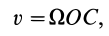или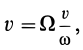

или

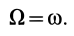
Вращение вокруг мгновенной оси должно иметь такое направление, чтобы скорость точки 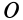имела такое же направление, что и скорость 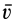. Отсюда получаем совпадение направлений вращения относительного и абсолютного вращений. Следовательно, 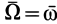. Таким образом, при сложении поступательного переносного и вращательного относительного движений твердого тела, у которого скорость поступательного движения перпендикулярна оси относительного вращения, эквивалентное абсолютное движение является вращением вокруг мгновенной оси, параллельной оси относительного вращения с угловой скоростью, совпадающей с угловой скоростью относительного вращения.

Такой же результат можно получить, если поступательное движение со скоростью 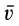заменить парой вращений 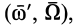, выбрав  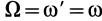. Два вращения с угловыми скоростям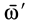и и 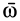можно отбросить, так как 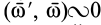, и абсолютным движением окажется вращение с угловой скоростью 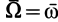. Скорость поступательного движения равна моменту пары вращений. Приравнивая их, получим  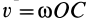 или

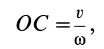
что совпадает с (12).

Еще одна интерпретация рассмотренного случая получается, если рассмотреть параллельный перенос скользящего вектора угловой скорости 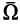в точку 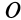. Такой перенос, как известно, следует компенсировать парой вращений, эквивалентной поступательному движению со скоростью .

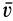На поступательное переносное и вращательное относительное с осью вращения, перпендикулярной к скорости переносного движения, разлагается плоское движение твердого тела. Так, плоское движение без скольжения колеса по прямой (рис. 100) можно составить из поступательного движения колеса вместе с центром 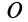со скоростью 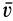и относительного вращательного

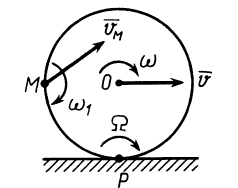
Рис. 100

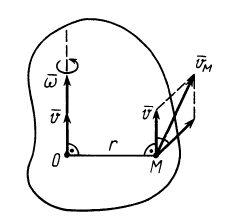
Рис. 101

вокруг оси, проходящей через точку с угловой скоростью . Это же движение можно рассматривать как вращение вокруг мгновенной оси, проходящей через 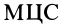, который совпадает с точкой 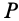. Угловая скорость этого абсолютного вращения 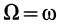, и оно имеет то же направление вращения, что и относительное вокруг оси, проходящей через точку 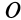. Если в качестве точки 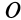используется другая точка колеса, например точка 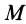, то изменится только скорость переносного поступательного движения. Она будет равна скорост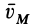и точки 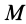. Угловая скорость  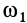вращения тела вокруг оси, проходящей через точку 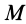, по величине и направлению будет той же самой, что и вокруг осей, проходящих через точк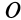и  и .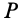

2. Винтовое движение. Движение, при котором скорость переносного поступательного движения тела параллельна оси относительного вращения, называется винтовым движением твердого тела (рис. 101). Ось вращения тела в этом случае называется винтовой осью. При винтовом движении тело движется поступательно параллельно оси винтового движения и вращается вокруг этой оси. Винтовое движение не приводится к какому-либо другому одному простому эквивалентному движению.

При винтовом движении векторы 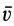и 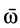могут иметь как одинаковые, так и противоположные направления. Винтовое движение тела характеризуется параметром винтового движения, которым считают величину 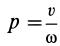. Если  и 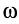 изменяются с течением времени, то и параметры винтового

движения являются переменными. В общем случае 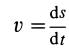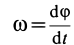и ,  и 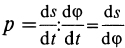, т. е. 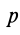есть перемещение тела вдоль оси винтового движения при повороте тела на один радиан.

Для скорости точки 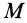тела, совершающего винтовое движение, по теореме сложения скоростей имеем

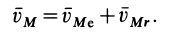
Но 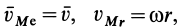, где 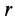—расстояние точки до винтовой оси. Скорост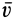и и 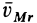 перпендикулярны. Следовательно,

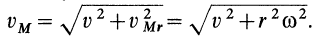
Учитывая, что 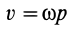, получаем

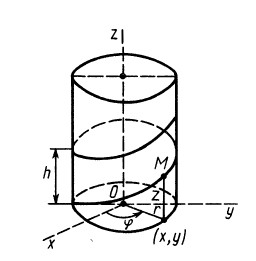
Рис. 102

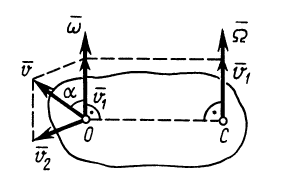
Рис. 103

Если тело вращается с постоянной угловой скоростью и имеет постоянную скорость поступательного движения, то такое движение тела называется постоянным винтовым движением. В этом случае точка тела при движении все время находится на поверхности кругового цилиндра с радиусом 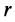. Траекторией точки является винтовая линия. Кроме параметра в рассматриваемом случае вводят шаг винта, т. е. расстояние, на которое переместится какая-либо точка тела при одном обороте тела вокруг оси винтового движения. Угол поворота тела 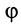при 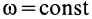вычисляется по формуле 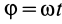. Для одного оборота тела 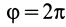. Необходимое для этого время

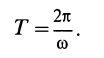
За время 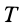точка переместится в направлении, параллельном винтовой оси, на шаг винта

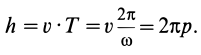
Отсюда получается зависимость шага винта от параметра винтового движения .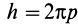

Уравнения движения точки 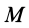тела по винтовой линии (рис. 102) в декартовых координатах выражаются в следующей форме:

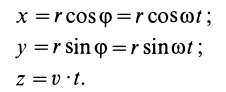
В этих уравнениях величины 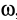, 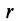и 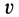 являются постоянными.

3. Общий случай. Пусть скорость переносного поступательного движения 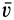и угловая скорость относительного вращения 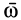образуют угол 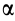. Случаи, когда 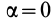, 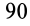и 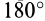, уже рассмотрены.

Разложим скорость 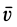(рис. 103) на две перпендикулярные составляющие 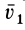и 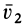, причем  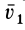направим параллельно 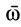. Тогда

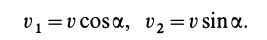
Переносное движение со скоростью 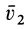и относительное вращение с угловой скоростью 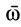эквивалентны вращению вокруг оси, проходящей через точку 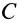с угловой скоростью  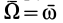(согласно случаю первому), причем .

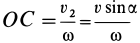Скорость поступательного движения 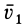имеют все точки тела. Таким образом, получено винтовое движение с винтовой осью, отстоящей от первоначальной оси вращения на величину

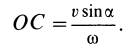
Параметр полученного винтового движения

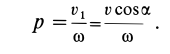
Общий случай переносного поступательного и относительного вращательного движений твердого тела оказался эквивалентным мгновенному винтовому движению.

Статические аналогии в кинематике

Рассмотренные случаи движений твердого тела показывают, что вектор угловой скорости тела со является вектором скользящим. В статике вектором скользящим является сила 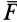, действующая на абсолютно твердое тело. Паре сил в статике соответствует пара вращений в кинематике, векторным моментом которой является" скорость поступательного движения тела. Эти аналогии позволяют без подробного рассмотрения сформулировать некоторые результаты сложения движений твердого тела, используя соответствующие теоремы, доказанные в статике.

Если тело участвует в 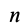вращениях с угловыми скоростям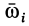и  и 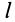поступательных движениях со скоростями 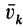, то по аналогии с приведением сил, приложенных к твердому телу, можно выбрать за центр приведения точку 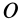тела и получить в качестве главного вектора угловых скоростей составляющих вращений угловую скорость

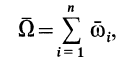
проходящую через точку 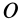. Главный момент при этом образуют все присоединенные пары вращений и скорости поступательных движений. Эквивалентная главному моменту скорость поступательного движения

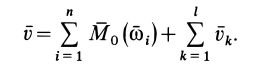
Полученное сложное движение тела можно дальше упростить. рно в общем случае приведется к винтовому движению, есл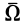и и 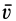не равны нулю и не перпендикулярны. В частных случаях, ес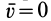ли или 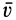перпендикулярно 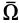, может получиться одно вращение. При 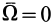получим одно эквивалентное поступательное движение со скоростью .

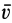Аналогично статическим инвариантам имеют место и кинематические инварианты. Так, инвариантности главного вектора сил в статике в кинематике соответствует инвариантность угловой скорости 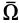, т. е. ее независимость от выбора центра приведения, вместе с которым тело совершает поступательное движение.