
Скорость при равнопеременном движении в физике - формулы и определения с примерами
Скорость при равнопеременном движении:
Самое простое из всех неравномерных движений — прямолинейное движение с постоянным ускорением, называемое равнопеременным. Как изменяется скорость тела при равнопеременном движении?
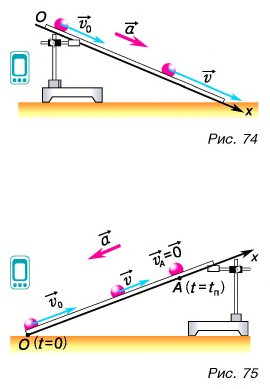
Рассмотрим движение стального шарика по наклонному желобу (рис. 74, 75). Опыт показывает, что ускорение шарика практически постоянно:

а, значит, движение шарика можно считать равнопеременным.
1. Пусть в начальный момент 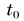 шарик находится в точке О и имеет начальную скорость
шарик находится в точке О и имеет начальную скорость 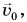 направленную вдоль желоба вниз (рис. 74).
направленную вдоль желоба вниз (рис. 74).
Найдем зависимость скорости движения шарика 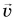 от времени t. Из определения ускорения
от времени t. Из определения ускорения 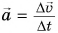 следует:
следует: 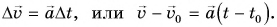
Отсюда, приняв 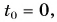 получим:
получим:
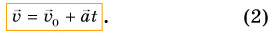
Такая зависимость в математике называется линейной. Значит, при движении с постоянным ускорением скорость тела линейно зависит от времени. Из равенств (1) и (2) следуют формулы для проекций:
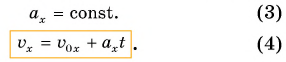
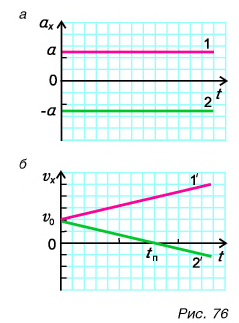
Учтем, что ось Ox направлена вдоль желоба вниз. Тогда 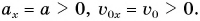 По формулам (3) и (4) построим графики проекций ускорения
По формулам (3) и (4) построим графики проекций ускорения 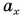 и скорости
и скорости 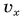 (рис. 76, а, б, графики 1 и 1'). Движение шарика — равноускоренное.
(рис. 76, а, б, графики 1 и 1'). Движение шарика — равноускоренное.
2. Придадим теперь начальную скорость 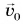 шарику, находящемуся в нижней точке желоба (рис. 75).
шарику, находящемуся в нижней точке желоба (рис. 75).
Двигаясь вверх, шарик будет постепенно терять скорость. В точке А он на мгновение остановится и начнет скатываться вниз. Точку А называют точкой поворота. Согласно рисунку 75 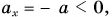
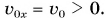 Тогда формулы (3) и (4) примут вид:
Тогда формулы (3) и (4) примут вид: 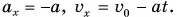 Им соответствуют графики 2 и 2' (рис. 76, а, б).
Им соответствуют графики 2 и 2' (рис. 76, а, б).
График 2' показывает: пока шарик двигался вверх, проекция скорости 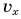 была положительной. Она уменьшалась и в точке поворота
была положительной. Она уменьшалась и в точке поворота 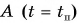 стала равной нулю. Затем направление скорости шарика изменилось на противоположное и при
стала равной нулю. Затем направление скорости шарика изменилось на противоположное и при 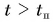 проекция скорости
проекция скорости 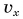 стала отрицательной.
стала отрицательной.
Что еще можно определить по графику проекции скорости?
При равномерном движении площадь фигуры под графиком 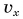 и осью времени (рис. 52) численно равна проекции перемещения
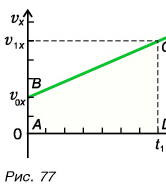
и осью времени (рис. 52) численно равна проекции перемещения 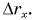 Это правило применимо и для равнопеременного движения. Тогда согласно рисунку 77 проекция перемещения
Это правило применимо и для равнопеременного движения. Тогда согласно рисунку 77 проекция перемещения 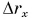 определяется площадью трапеции ABCD. Эта площадь равна полусумме оснований трапеции, умноженной на ее высоту
определяется площадью трапеции ABCD. Эта площадь равна полусумме оснований трапеции, умноженной на ее высоту 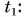

Разделив 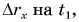 получим проекцию средней скорости перемещения при равноускоренном движении:
получим проекцию средней скорости перемещения при равноускоренном движении:

При движении с постоянным ускорением соотношение (6) выполняется не только для проекции, но и для векторов скорости:

Средняя скорость движения с постоянным ускорением равна полусумме начальной и конечной скоростей.
Главные выводы
- При движении с постоянным ускорением скорость линейно зависит от времени.
- Средняя скорость равнопеременного движения равна полусумме начальной и конечной скоростей.
- Площадь под графиком проекции скорости равнопеременного движения численно равна проекции перемещения.
Пример решения задачи:
На участке пути 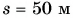 водитель равномерно снизил скорость движения автомобиля от
водитель равномерно снизил скорость движения автомобиля от 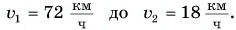 Определите характер движения автомобиля. Найдите направление и модуль ускорения его движения.
Определите характер движения автомобиля. Найдите направление и модуль ускорения его движения.
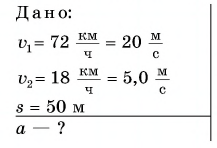
Решение
Автомобиль двигался равнозамедленно. Ускорение автомобиля было направлено противоположно его скорости. Модуль ускорения:
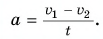
При равнопеременном движении без изменения направления путь 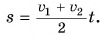 Время
Время 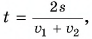 ускорение
ускорение 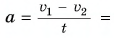
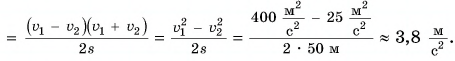
Ответ: 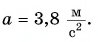
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |