Скалярные и векторные величины и действия над ними в физике с примерами

Содержание:

Скалярные и векторные величины:

В 7-м и 8-м классах мы рассматривали различные физические величины. Для одних величин достаточно знать их числовое значение и единицу измерения. Например, масса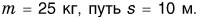

На рисунках 14, а и 14, б девочка действует на санки силой, имеющей одно и то же числовое значение. Но в первом случае санки лишь немного погрузились в снег, а во втором — пришли в движение. Значит, сила определяется не только числовым значением, но и направлением. Сила — величина векторная.

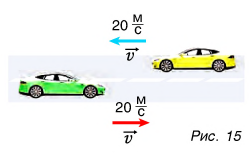
Векторной величиной является и скорость движения тел (рис. 15), и многие другие физические величины.

Что нужно знать о векторных величинах (векторах)

Векторы характеризуются модулем и направлением в пространстве

Модулем вектора называется его числовое значение.

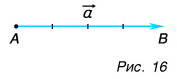
Вектор изображают в виде направленного отрезка (стрелки). Стрелка указывает, куда направлен вектор (рис. 14, 15). Длина стрелки характеризует модуль вектора (рис. 16). Над буквенным обозначением вектора ставят стрелку, например:  

Модуль вектора обозначают той же буквой, но без стрелки над ней или символом 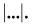 Например, модуль вектора 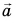на рисунке 16 равен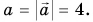

Модуль любого (не равного нулю) вектора — число положительное.

Векторы равны между собой, если равны их модули и одинаковы направления

Равные векторы лежат на одной и той же прямой или на параллельных прямых и направлены в одну и ту же сторону. На рисунке 17 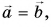 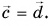 Однако, несмотря на равенство модулей, 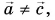так как у векторов 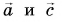различные направления.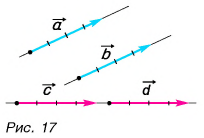  

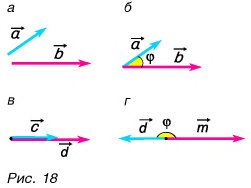
Угол между векторами

Чтобы найти угол 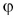между векторами (рис. 18, а), нужно совместить их начала (рис. 18, б). Если направления векторов одинаковы, то 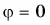(рис. 18, в), если противоположны, то 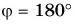(рис. 18, г).

  

Умножение вектора на число

Произведение вектора 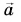на число 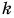есть вектор 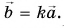Чему в равен его модуль? Куда направлен вектор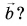

Модуль вектора 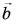равен

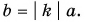
Если 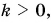то вектор 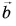направлен так же, как вектор 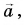а если 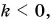то противоположно ему.

На рисунке 19 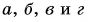показаны результаты умножения вектора 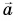на 2, на 0,5, на (-3) и на (-1) соответственно. 

Противоположные векторы

Вектор 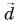называется противоположным вектору 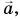если 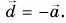У векторов 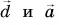одинаковые модули, но противоположные направления (рис. 19, а, г).

Сложение векторов

В 7-м классе вы складывали силы, направленные или одинаково, или в противоположные стороны. Результатом сложения в первом случае была сила, модуль которой равен 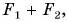а во втором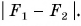

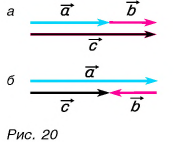
То же самое получается и при сложении векторов  (рис. 20). Если они направлены одинаково (рис. 20, а), то их сумма 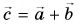имеет модуль 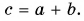Если же направления векторов 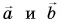противоположны (рис. 20, б), то модуль их суммы 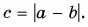Обратите внимание: в последнем случае вектор 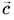направлен так, как вектор с большим модулем (т. е. как вектор ).  

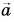А как сложить векторы, направленные под любым углом друг к другу? Для этого можно использовать любое из двух следующих далее правил. 

Правило параллелограмма

Совместим начала векторов 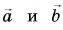(рис. 21, а), сохраняя их направления (рис. 21, б). Построим параллелограмм ABCD, принимая векторы 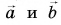за его стороны. Сумма векторов 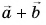есть вектор 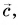совпадающий с диагональю АС параллелограмма: 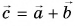(см. рис. 21, б).

Правило треугольника

Совместим конец вектора 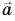с началом вектора 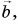сохраняя их направления (рис. 21, в). Вектор 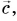проведенный из начала вектора 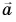в конец вектора  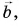равен сумме 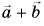(см. рис. 21, в).

Из рисунков 21, б и 21, в ясно, что правило треугольника и правило параллелограмма дают одинаковые результаты. А как найти разность векторов?

Вычитание векторов

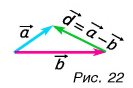
Пусть начала векторов 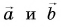совмещены (рис. 22). Проведем вектор 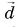из конца вычитаемого вектора 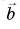в конец уменьшаемого вектора 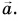Вектор 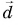есть искомая разность:  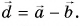Докажите с помощью построения, что Такой способ вычитания векторов очень удобен.

Правило многоугольника

Чтобы найти сумму нескольких векторов (например, 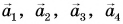), каждый следующий вектор нужно проводить из конца предыдущего (рис. 23). Замыкающий вектор 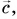проведенный из начала первого вектора 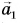в конец последнего 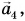есть сумма данных векторов: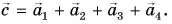 

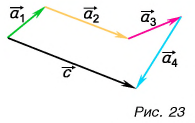
Правило многоугольника следует из правила треугольника.

Модуль суммы векторов

Не путайте модуль суммы векторов, т. е. 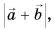и сумму их модулей  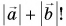Равенство  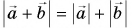выполняется только для одинаково направленных векторов (см. рис. 20, а на с. 13). Во всех остальных случаях 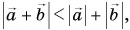т. е. модуль суммы векторов меньше суммы их модулей. Так получается потому, что в любом треугольнике (см. рис. 21, в) длина одной стороны меньше суммы длин двух других сторон. Проверьте это на примерах.

Нуль-вектор

Пусть вектор 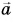равен вектору 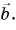Тогда их разность 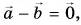т. е. нуль-вектору.

Главные выводы:

1. Векторные величины характеризуются модулем и направлением, скалярные — только числовым значением.
2. Сумму двух векторов находят по правилу параллелограмма или треугольника.
3. Разность двух векторов находят, проводя вектор из конца вычитаемого вектора в конец уменьшаемого (при совмещенных началах векторов).
4. Разность векторов 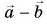можно найти как сумму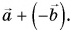
5. Произведение вектора 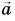на число 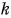есть вектор 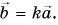При 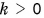направления векторов 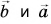совпадают, а при 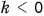— противоположны. Модуль вектора 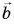равен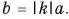

Скалярные и векторные величины

К пониманию того, что для описания природы нужно использовать язык математики, ученые пришли давно. Собственно, некоторые разделы математики и были созданы для того, чтобы описывать природу кратким и доступным языком. Так, для определения мгновенной скорости, работы переменной силы, объема тел неправильной формы и т. д. были созданы дифференциальное и интегральное исчисления. Для более наглядного описания физических процессов научились строить графики функций, а для быстрой обработки результатов эксперимента придумали методы приближенных вычислений. Вспомним скалярные и векторные величины, без которых вам не обойтись при изучении курса физики 10 класса.

Физические величины, используемые в физике для количественной характеристики физических явлений и объектов, делятся на два больших класса: скалярные величины и векторные величины.

К скалярным величинам, или скалярам (от лат. scalaris — ступенчатый), относятся величины, которые определяются только значением. Например, масса тела — скалярная величина, и если мы говорим, что масса тела равна двум килограммам (m=2 кг), то полностью определяем эту величину. Сложить две скалярные физические величины означает сложить их значения, представленные в одинаковых единицах. Понятно, что складывать можно только однородные скаляры (например, нельзя складывать массу и время, плотность и работу и т. д.).

Для определения векторных величин важно знать не только их значения, но и направления. Вектор (от лат. vector — носитель) — это направленный отрезок, то есть отрезок, имеющий и длину, и направление. Длину направленного отрезка называют модулем вектора. Обозначают векторные величины буквами греческого и латинского алфавитов, над которыми ставят стрелки, или полужирными буквами. Например, скорость записывают так: v или 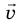; модуль вектора скорости соответственно обозначают как v.

Правила сложения (вычитания) векторов отличаются от правил сложения (вычитания) скалярных величин.

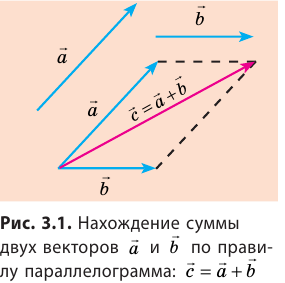
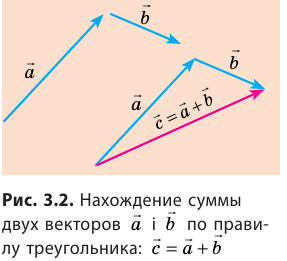
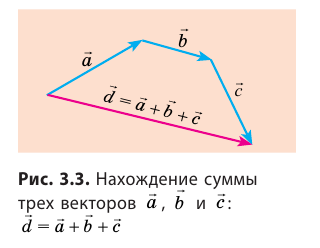
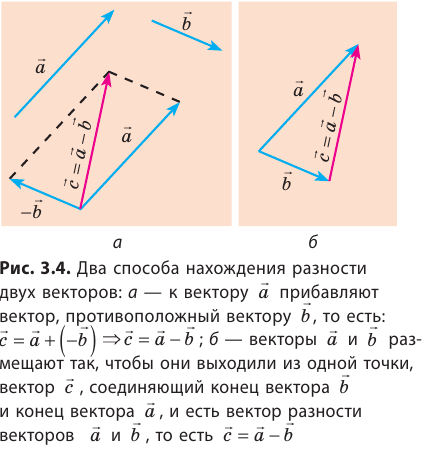
Сумму двух векторов находят по правилу параллелограмма или по правилу треугольника (рис. 3.1, 3.2). Как найти сумму нескольких векторов, показано на рис. 3.3, как найти разность двух векторов, показано на рис. 3.4.

В результате умножения векторной величины 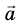на скалярную величину k получается вектор 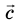(рис. 3.5).

Обратите внимание! Единица произведения векторной и скалярной величин определяется как произведение единицы одной величины на единицу другой. Например, нужно найти перемещение самолета, который в течение 0,5 ч летит на север со скоростью 500 км/ч. Вектор перемещения: 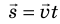. Поскольку t > 0, то вектор перемещения 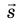будет направлен в ту же сторону, что и вектор скорости 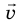, а модуль вектора перемещения будет равен: s v = =t 500 км /ч⋅ = 0 5, ч к 250 м.

• Заказать решение задач по физике

Как найти проекции вектора на оси координат

Осуществлять математические операции с векторами гораздо сложнее, чем со скалярами, поэтому, решая задачи, от векторных физических величин переходят к их проекциям на оси координат.

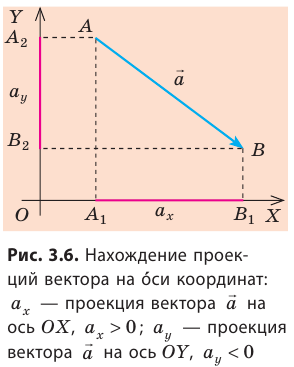
Пусть вектор 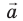лежит в плоскости XОY (рис. 3.6). Опустим из точки А (начало вектора 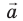) и точки В (конец вектора 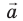) перпендикуляры на ось ОX. Основания этих перпендикуляров — точки 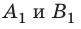— проекции точек А и В на ось ОX, а отрезок 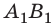— проекция вектора 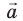на ось ОX. Проекцию вектора обозначают той же буквой, что и вектор, с указанием оси в нижнем индексе, например: 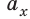. Если из начала и конца вектора 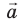провести перпендикуляры к оси ОY, получим отрезок 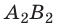— проекцию вектора 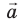на ось ОY ( 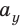). Знак проекции вектора зависит от направлений вектора и оси координат. Если от проекции начала вектора до проекции его конца нужно двигаться в направлении оси координат, то проекция вектора на эту ось считается положительной, а если наоборот, то проекция вектора считается отрицательной (см. рис. 3.6).

В общем случае проекцию вектора находят обычными геометрическими методами (рис. 3.7, а). На практике часто приходится иметь дело со случаями, когда вектор параллелен или перпендикулярен оси координат.

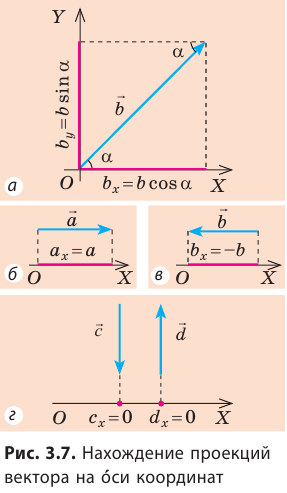
Если вектор параллелен оси координат, а его направление совпадает с направлением оси, то его проекция на эту ось положительна и равна модулю вектора (рис. 3.7, б). Если направление вектора противоположно направлению оси координат, то его проекция на эту ось равна модулю вектора, взятому с противоположным знаком (рис. 3.7, в). Если же вектор перпендикулярен оси координат, то его проекция на эту ось равна нулю (рис. 3.7, г). Очень важным свойством проекций является то, что проекция суммы двух векторов (рис. 3.8) или нескольких векторов на координатную ось равна алгебраической сумме проекций этих векторов на данную ось.

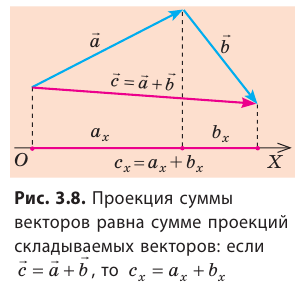
Именно это свойств позволяет заменять в уравнении векторные величины их проекциями — скалярными величинами и далее решать полученное уравнение обычными алгебраическими методами.