Системы неравенств - определение и вычисление с примерами решения

Содержание:

Системы неравенств и совокупность неравенств

Исследование. Если альпинисты увеличат скорость на 1км/ч, то путь 4 км до вершины они преодолеют быстрее чем за 2 часа. Если же они уменьшат скорость на 1 км/ч, то не смогут добраться до вершины за 2 часа. С какой скоростью движутся альпинисты? Решение: Примем за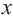

Если скорость увеличится на 1 км/ч, то длина пройденного пути будет больше 4-х км и соответствующее неравенство примет вид: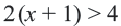

Если скорость уменьшится на 1 км/ч, то длина пройденного пути будет меньше 4-х км и соответствующее неравенство примет вид: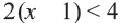

По условию задачи нужно найти такое значение 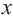, которое удовлетворяло бы каждому из неравенств: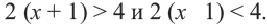

Неравенства, объединенные союзом 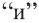записывают с помощью фигурной скобки и говорят, что они образуют систему неравенств.

В данной задаче нужно решить систему неравенств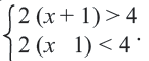

Если каждое неравенство системы заменить на равносильное неравенство, то получим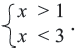 Изобразим на числовой прямой множество решений неравенств, входящих в систему, и найдем их пересечения (общую часть).

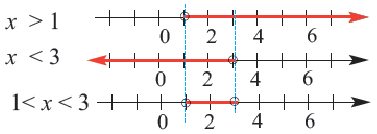
Для того, чтобы решить систему неравенств нужно найти множество решений каждого неравенства и найти пересечение этих множеств, то есть, общую часть.

Ответ: Решение системы промежуток .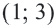

Совокупность неравенств

Задача. Наргиз и Эльшан играют в игру, построенную на числах. Каждый берег карточку с числом и прибавляет к нему 5. Если ответ будет меньше 10-ти или же больше 15-ти, то владелец карточки зарабатывает очко. Выразите с помощью неравенства ситуацию, когда Эльшан взяв одну карточку заработал очко.

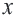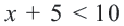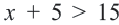Решение: Пусть число на карге будет . Требуемую ситуацию можно выразить неравенствами или . Союз "или" и соответствующие неравенства записываются с помощью скобки 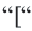и образуют совокупность неравенств. Чтобы решить совокупность неравенств, нужно найти множество решений каждого неравенства, а потом найти объединение этих множеств. Решим: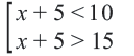

Решением данной совокупности неравенств будет множество: .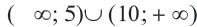

Пример.

Решите неравенство: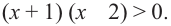

Решение: Для того, чтобы произведение двух множителей было положительным, нужно чтобы множители были одинакового знака. То есть, множител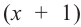и и должны быть или оба положительными, или отрицательными.

Данное неравенство сводится к решению совокупности: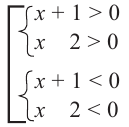

Решение 1-ой системы совокупности: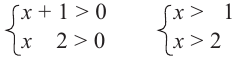

Геометрическое изображение:

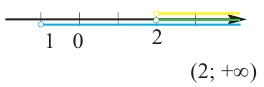Решение 2-ой системы совокупности:

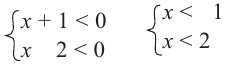
Геометрическое изображение:

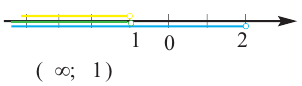Решением данной совокупности будет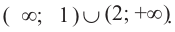

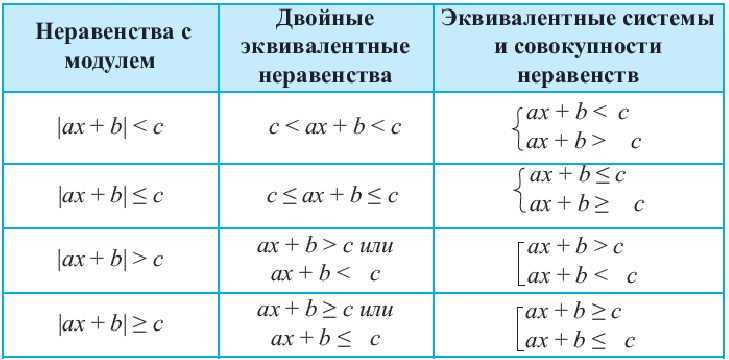
Неравенства, содержащие переменную под знаком модуля

Система неравенств, совокупность неравенств

Пример 2.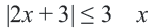

Решение: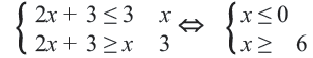

Пример 3.

Решение: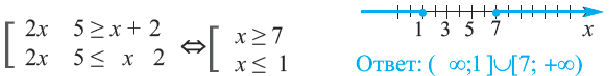

Линейные неравенства с двумя переменными

Неравенства вида 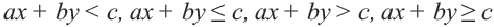называются линейными неравенствами с двумя переменными. Решением неравенства называется пара 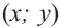, обращающая данное неравенство в верное числовое неравенство. С помощью графика линейного уравнения 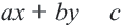в прямоугольной системе координат можно показать все решения линейного неравенства с двумя переменными. Например, покажем множество решений неравенства 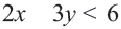с помощью графика линейного уравнения с двумя переменными. График уравнения 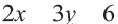образует линию границы.

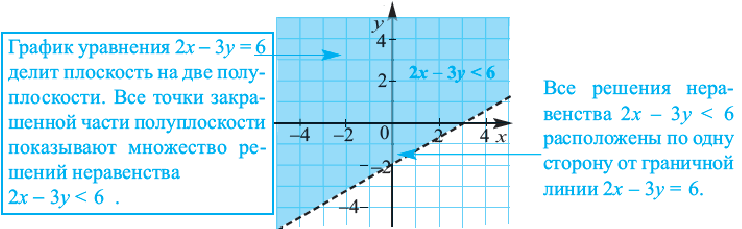
• Чтобы убедиться в правильности выбора полуплоскости, соответствующей решению неравенства, выбираются пробные точки в каждой из полуплоскостей. Закрашивается та полуплоскость, в которой расположена точка, удовлетворяющая данному неравенству.

• Если неравенство выражается знаками 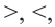то множество точек, образующих линию границы, не принадлежат множеству решений и график уравнения 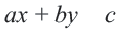изображается пунктирной линией.

• Если неравенство выражается знаками 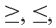то множество точек образующих линию границы принадлежат графику и изображаются сплошной линией

Пример 1.

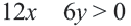
1. Решим неравенство относительно переменной :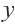

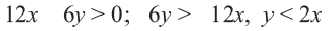
2. Нарисуем график уравнения 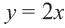пунктирной линией.

3. Проверим неравенство в точке 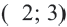. Левая часть неравенства: 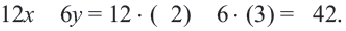Правая часть: 0. Неравенство 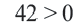неверное. Значит, должна быть закрашена не та полуплоскость, в которой находится точка 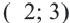, а другая.

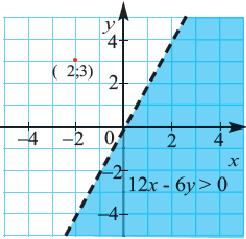
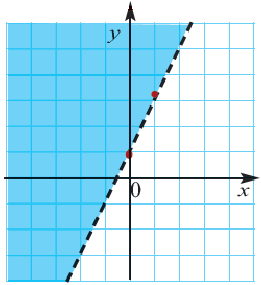
Пример 2. Напишите неравенство, соответствующее графику.

1. Определим уравнение 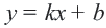граничной линии. График пересекает ось 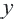в точке 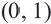. Значит, 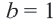. По точке 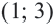графика можно определить, что 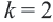. То есть из уравнения 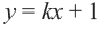по координатам точки 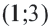получим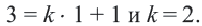

Уравнение линии границы: 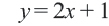. Так как линия границы нарисована пунктирами, то точки принадлежащие уравнению 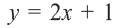, не входят во множество решений неравенства. Выберем пробную точку 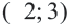из закрашенной части и проверим. Левая часть: 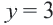, правая часть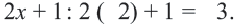

Левая часть 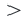правой части, значит, 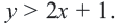То есть, закрашенная часть на рисунке является множеством решений неравенства .

• Заказать решение задач по высшей математике

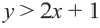Прикладные задания.

Пример 1. Билет в театр для взрослых стоит 16 манат, а детский - 4 манат. Деньги, вырученные от продажи билетов в кассе, составляют не более 160 манат. Определите различные варианты количества проданных билетов. Числовые информации и переменные, соответствующие условию задачи:

Математическая запись: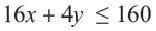

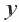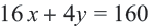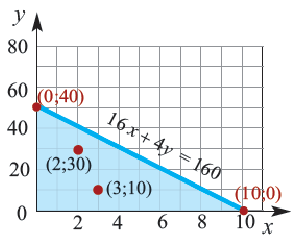
1. Чтобы решить неравенство, выразим из уравнения , получим 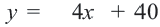и построим график полученной линейной функции. Количество билетов не может быть отрицательным числом. Поэтому достаточно построить график только в I четверти. Определим точки пересечения графика с осями координат: 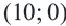и 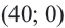. Соединим эти точки отрезком прямой.

2. Закрасим фигуру, заданную графиком и осями координат.

3. Любые целые значения 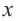и 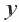, взятые из закрашенной части, являются решением этого неравенства. Точка 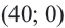соответствует случаю, когда все билеты были куплены для детей, а точка 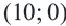случаю, когда все билеты были куплены для взрослых. А также любая точка, взятая из закрашенной части удовлетворяет неравенству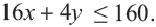

Системы линейных неравенств с двумя переменными

Решением системы линейных неравенств с двумя переменными называется множество пар чисел 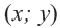, которые удовлетворяют каждому неравенству системы. На примере покажем графическое решение системы линейных неравенств.

Пример 1.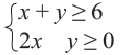

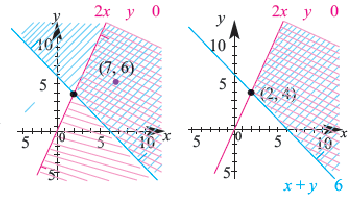
1. С помощью граничной прямой 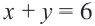построим график, соответствующий неравенству 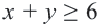, а соответствующую площадь представим голубыми линиями.

2. С помощью уравнения 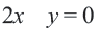построим график, соответствующий неравенству 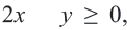а соответствующую площадь представим красными линиями.

3. Множеством решений данной системы неравенств будет часть плоскости, закрашенная обоими цветами.

4. Выберем отсюда одну точку, например 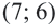, и проверим, удовлетворяют ли координаты системе неравенств:

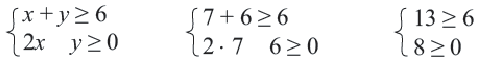
Каждая пара 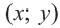из закрашенной обоими цветами части является решением данных неравенств системы. Согласно условиям неравенств граничные линии тоже принадлежат решению системы, поэтому они нарисованы сплошными линиями.

Пример 2. Изобразите графически на координатой плоскости неравенство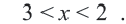

1. Запишем двойное неравенство 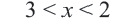в виде системы неравенств: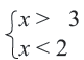

2. Изобразим неравенство 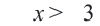графически: Нарисуем на координатной плоскости пунктирной линией прямую, соответствующую уравнению Все точки полуплоскости, расположенные правее от этой прямой будут решениями неравенства

3. Изобразим неравенство 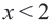графически: прямую, соответствующую уравнению 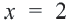, нарисуем в прямоугольной системе координат пунктирной линией. Все точки полуплоскости, расположенные левее от этой прямой будут решениями неравенства .

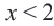4. Часть плоскости, соответствующая неравенствам 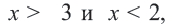изображает решение неравенства 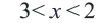на координатной плоскости. 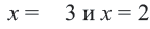не принадлежат графику.

5. Проверка: проверим в точке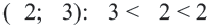

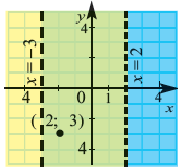
График системы линейных неравенств, соответствующий реальным жизненным ситуациям, в большинстве случаев строится в первой четверти координатной плоскости.

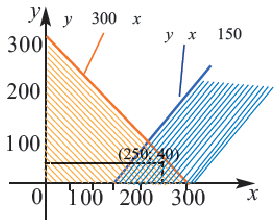
Пример 3. На одном из двух конвейеров производят кастрюли из нержавеющей стали, а на другом медные кастрюли. Если каждый из конвейеров работает на полную мощность, то ежедневно производится не более 300 кастрюль. Так как потребность в кастрюлях из нержавеющей стали больше, их ежедневно производят больше чем медных, но не меньше 150 штук. Напишите систему неравенств, показывающую ежедневное количество производимых кастрюль, и изобразите графически.

Решение: 1) Примем за 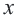- количество кастрюль из нержавеющей стали; за 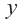количество медных кастрюль. Согласно условию задачи, можно написать следующую систему неравенств.

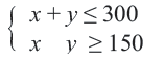
2) Решение неравенства 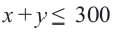изображает прямая 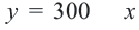и часть полуплоскости, расположенная ниже этой прямой. Решение неравенства 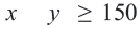изображает прямая 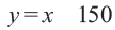и часть полуплоскости, расположенная ниже этой прямой. Решением системы 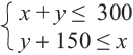является часть плоскости, закрашенная двумя цветами и охватывающая решения соответствующих обоих неравенств, включая граничные прямые.

3. С помощью пробной точки 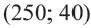проверим систему неравенств.

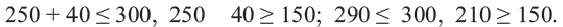
Решение системы неравенств найдено верно.