Система сходящихся сил в теоретической механике

Содержание:

Система сходящихся сил:

Рассмотрим одну из важных систем сил — систему сходящихся сил. Для этой системы сил следует рассмотреть приведение ее к простейшему виду и установить условия равновесия.

Системой сходящихся сил (или пучком сил) называют такую систему сил, линии действия которых пересекаются в одной точке — центре пучка. Сходящиеся системы сил могут быть пространственными и плоскими, т. е. расположенными в одной плоскости.

Приведение к равнодействующей силе

Рассмотрим общий случай пространственной системы сходящихся сил. Так как сила, действующая на твердое тело, есть вектор скользящий, то можно считать, что силы системы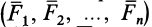

Применяя к первым двум силам пучка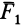

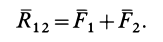
Затем по правилу параллелограмма складываем силы 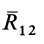и  и 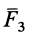получаем их равнодействующую:

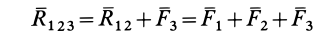
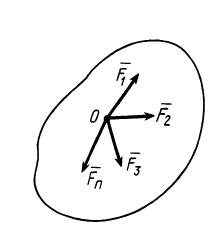
Рис. 12

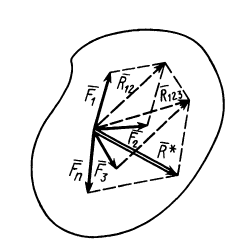
Рис. 13

и т. д. Продолжая процесс векторного сложения сил для всех 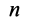сил, получим

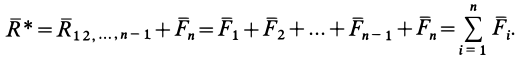
Таким образом, система 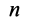сходящихся сил эквивалентна одной силе 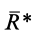, которая и является равнодействующей этой системы сил.

Процесс последовательного применения к силам правила параллелограмма, или их векторного сложения, приводит к построению силового многоугольника из заданных сил. В силовом многоугольнике конец одной из сил служит началом другой (рис. 14). Равнодействующая сила 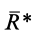в силовом многоугольнике соединяет начало первой силы с концом последней, т. е. изображается замыкающей силового многоугольника, который в общем случае является незамкнутым. Силы в силовом многоугольнике можно изображать в любой последовательности. От этого изменится форма силового многоугольника, а замыкающая не изменится; следовательно, не изменится и равнодействующая сила.

Для пространственной системы сходящихся сил силовой многоугольник является пространственной фигурой, для плоской— плоской. Для плоской системы сходящихся сил равнодействующую силу можно определить графически путем построения замыкающей силового многоугольника в выбранном для сил масштабе. Для пространственной системы сходящихся сил пришлось бы силовой многоугольник строить в пространстве из стержней.

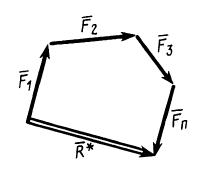
Рис. 14

Итак, система сходящихся сил в общем случае приводится к одной силе—равнодействующей этой системы сил, которая изображается замыкающей силового многоугольника, построенного на силах системы. Линия действия равнодействующей силы проходит через центр пучка параллельно замыкающей силового многоугольника.

Для аналитического определения равнодействующей силы следует выбрать систему прямоугольных осей координат и воспользоваться известной из геометрии теоремой о том, что проекция замыкающей любого многоугольника на какую-либо ось равна алгебраической сумме проекций составляющих его сторон на ту же ось.

Так как равнодействующая сила 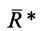является замыкающей силового многоугольника, или векторной суммой сил, то

Проецируя векторы векторного равенства на прямоугольные оси координат, согласно теореме о проекции замыкающей получим

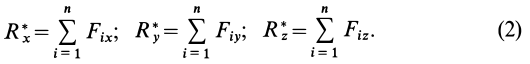
По проекциям определяем модуль равнодействующей силы и косинусы углов ее с осями координат по формулам

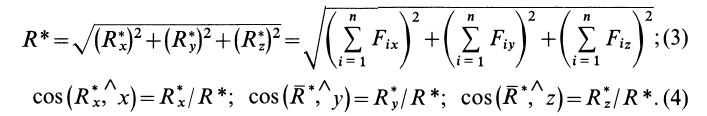
В формуле (3) перед квадратным корнем всегда берут знак плюс, так как определяется модуль равнодействующей силы.

В случае плоской системы сходящихся сил одну из координатных осей, обычно 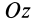, выбирают перпендикулярной силам, тогда каждая из сил пучка даст проекцию на эту ось, равную нулю, а следовательно, будет равна нулю и проекция равнодействующей силы на эту ось, т. е.

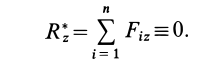
Условия равновесия системы сходящихся сил

Для равновесия системы сходящихся сил, приложенных к твердому телу, замыкающая силового многоугольника, изображающая равнодействующую силу, должна обратиться в точку, т. е. конец последней силы в многоугольнике должен совпасть с началом первой силы. Такой силовой многоугольник называют замкнутым (рис. 15). Получено условие равновесия сходящихся сил в геометрической форме: для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым. Для случая трех сходящихся сил при равновесии должен быть замкнутым силовой треугольник, построенный из трех сил.

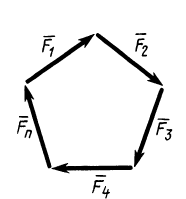
Рис. 15

Для определения неизвестных сил при равновесии более предпочтительным является использование условий равновесия системы сходящихся сил в аналитической форме. Так как при равновесии системы сходящихся сил равнодействующая сила должна быть равна нулю (силовой многоугольник замкнут), то из этого следует, что равно нулю подкоренное выражение в (3), состоящее из суммы положительных величин. Таким образом, равны нулю квадраты каждой из величин подкоренного выражения, а следовательно, равны нулю и сами величины. Получаем условия равновесия пространственной системы сходящихся сил в аналитической форме:

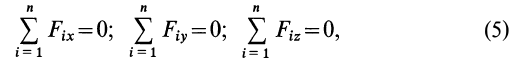
т. е. для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций сил на каждую из трех прямоугольных осей координат были равны нулю.

В случае плоской системы сходящихся сил одну из осей координат, обычно 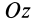, выбирают перпендикулярной силам, а две другие оси—соответственно в плоскости сил. Тогда третье условие из (5) превратится в тождество 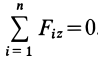. Отбрасывая его, получаем

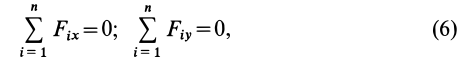
т. е. для равновесия плоской системы сходящихся сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных координатных осей, лежащих в плоскости сил, были равны нулю.

Проецирование силы на оси координат

Если дана сила 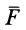, то ее проекции на прямоугольные оси координат вычисляются по формулам

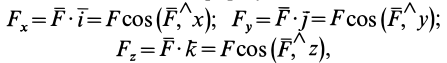
где 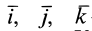— единичные векторы, направленные по осям координат. Косинусы углов силы с осями координат удовлетворяют условию

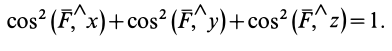
Из трех углов независимыми являются только два.

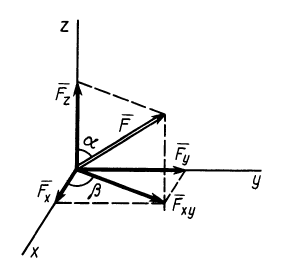
Рис. 16

При проецировании силы на прямоугольные оси координат целесообразно использовать тоже два угла. Для этого предварительно силу разлагают на две взаимно перпендикулярные составляющие, одна из которых параллельна какой-либо оси координат, например 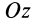, а другая находится в координатной плоскости двух других осей, в нашем случае — координатной плоскости 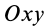(рис. 16). Получаем

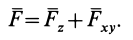
Проецируя векторы векторного равенства на координатные оси, имеем

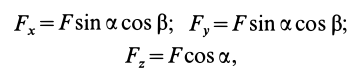
так как

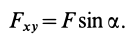
При проецировании использованы только два угла: 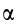и .

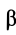Векторные величины 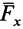, , 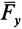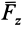называются составляющими силы 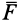по осям координат. Скалярные величины 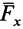, , 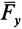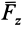являются проекциями силы 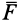на оси координат. Таким образом, силу на оси координат проецируют обычно в два приема. Сначала ее проецируют на одну из осей и на координатную плоскость двух других осей. Проекция силы на плоскость является вектором. Этот вектор затем проецируют на оси координат, расположенные в плоскости.

Пример 1.

Подъемный кран, имеющий вертикальную ось вращения 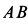, состоит из стержней, скрепленных шарнирами. Ось крана закреплена с помощью подпятника 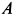и подшипника 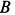(рис. 17, а). Считая стержни и весь кран невесомыми, определить силы реакций в подпятнике и в подшипнике, усилия в стержнях 1, 2, 3, 4, если известны размеры 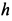и 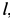, а также углы 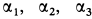. Стержни 2 и 5 горизонтальны. Кран с помощью троса 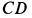удерживает груз, сила тяжести которого равна .

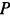Решение. Считая кран твердым телом, освободим его от связей, которыми являются подпятник и подшипник, заменив их силами реакций связей. Сила реакции подшипника (цилиндрический шарнир) перпендикулярна его оси. Направление силы реакции подпятника заранее не известно и подлежит определению. На весь кран, находящийся в равновесии, действуют три силы: 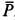, , 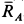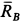(рис. 17,6). Линии действия этих сил должны пересекаться в одной точке, т. е. линия действия силы  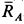должна пройти через точку 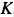, в которой пересекаются линии действия сил 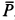и 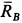. Три силы должны образовывать также замкнутый силовой треугольник. Отложим силу 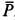в выбранном масштабе и проведем через ее начало и конец линии, параллельные силам  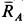и 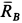. В полученном силовом треугольнике три силы должны быть направлены друг за другом (рис. 17, в). Из полученного прямоугольного треугольника находим

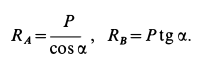
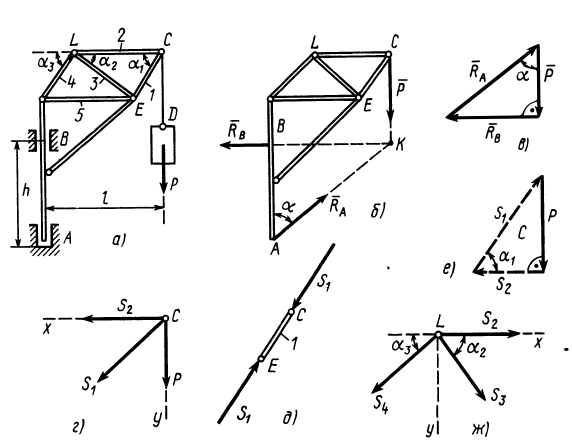
Рис. 17

Из геометрического треугольника

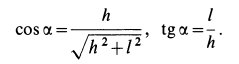
Для определения усилий в стержнях 1 и 2 применим метод вырезания узлов. Для этого рассмотрим равновесие отдельного шарнира или узла С. На этот узел действуют сила Р через трос и силы реакций стержней 1 и 2, которые следует мысленно отбросить. Силы реакций стержней на узел должны быть направлены по стержням, так как на эти стержни между их шарнирами другие силы не действуют. Стержни являются шарнирными. (Условимся силы реакций стержней направлять от узла (рис. 17, г) и знак вектора у сил на рисунке не ставить, чтобы не увеличивать без необходимости число обозначений для одинаковых по числовому значению сил.)

Выбрав в точке 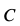оси координат, составим условия равновесия для плоской системы сходящихся сил, действующих на узел :

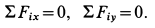
Эти условия в рассматриваемом случае принимают форму в проекциях на оси:

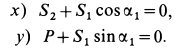
Из полученных уравнений получаем:

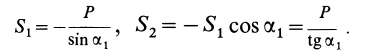
Знак 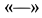у 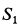показывает, что направление этой силы противоположно принятому, т. е. направлено к узлу. Рассматривая равновесие отдельного стержня 1, убеждаемся, что на него действуют только две силы со стороны узлов и 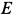. Эти силы должны быть при равновесии равны по модулю и противоположны по направлению. Узел действует на стержень 1 с силой 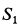 , противоположной по направлению силе действия стержня на узел 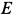(рис.17, д). Таким образом, получаем, что при рассмотрении равновесия узла , когда 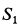имеет отрицательное значение, стержень 1 будет сжат;  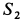получили с плюсом. Следовательно, стержень 2 будет испытывать растяжение.

На узел действуют три силы, и они поэтому должны образовывать замкнутый силовой треугольник. Построение силового треугольника следует начать с известной силы 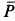, проводя через ее концы линии, параллельные неизвестным по значению силам реакций стержней (рис. 17, е). Из силового треугольника можно определить силы 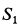и .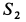

Из уравнений равновесия или силового треугольника можно определить только две неизвестные силы. Поэтому при дальнейшем решении задачи следует переходить к рассмотрению равновесия узла, на который действуют не более двух неизвестных сил. Таким узлом является узел 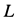. На узел 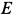действуют три неизвестные силы. При рассмотрении равновесия узла 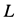будем направлять силы реакций стержней опять от этого узла (рис. 17,ж) независимо от ранее полученных знаков для них. В уравнения равновесия уже известную силу 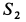следует подставить со знаком плюс, полученным для нее ранее. Условия равновесия сил, действующих на узел 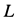, имеют форму:

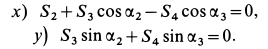
Из этих уравнений находим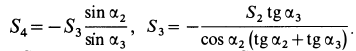

Подставляя в выражение для 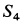полученное значение 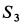, получим

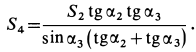
Усилие 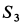 при положительном 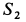отрицательно. Следовательно, стержень 3 сжат. Усилие 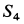положительно. Поэтому стержень 4 растянут.

Для узла 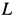можно построить также замкнутый силовой треугольник и решить задачу нахождения неизвестных сил геометрически.

Пример 2.

Груз с силой тяжести 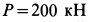 прикреплен с помощью троса к шарниру 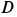, который крепится к вертикальной стене тремя стержнями, два из которых расположены в горизонтальной плоскости, а третий — в вертикальной, с помощью шарниров. Сила сопротивления груза от ветра 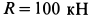горизонтальна и параллельна стене. Определить силу натяжения троса и усилия в стержнях, считая стержни невесомыми, если 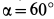, 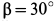(рис. 18, а).

Решение. На находящийся в равновесии груз 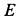действует система трех сходящихся сил, расположенных в вертикальной_ плоскости, параллельной стене. Это сила тяжести 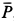, сила сопротивления 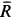и сила натяжения троса 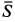, направленная по нему (рис. 18,6). Сила 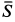должна уравновесить равнодействующую сил 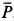и 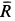. Следовательно,

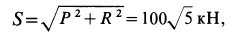
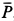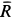так как силы и перпендикулярны. Сила 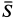составляет с вертикалью угол 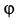, для которого

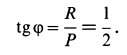
Рассмотрим равновесие шарнира 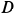, на который действуют силы реакции трех стержней 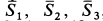, направленные по стержням, и сила натяжения троса, равная 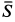(рис. 18, в). Имеем пространственную систему сходящихся сил, условия равновесия которой имеют форму

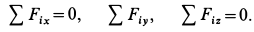
В рассматриваемом случае для выбранных осей координат имеем:

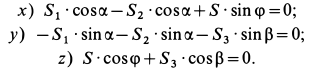
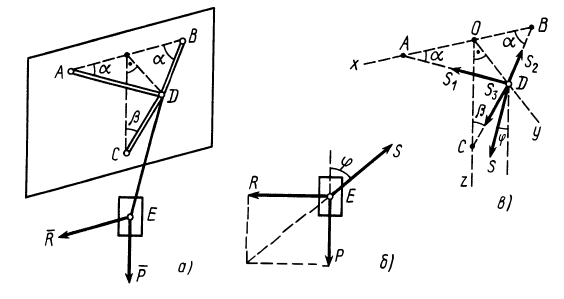
Рис. 18

Так как

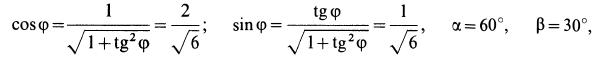
то система уравнений принимает форму

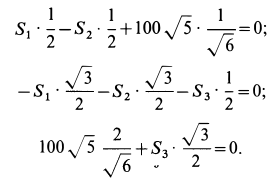
Решая эту систему уравнений, получаем:

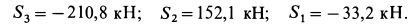
Усилия в стержнях направляли от рассматриваемого узла и получил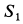и и 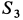со знаком минус, a  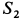— со знаком плюс. Это служит указанием, что стержни 1 и 3 подвергаются сжатию, а стержень 2 — растяжению.

Силы, сходящиеся в одной точке

Если на точку А действуют n сил, расположенных в одной плоскости (рис. 22), то эти силы можно сложить геометрически, построив многоугольник векторов, который в нашем случае называется многоугольником сил.

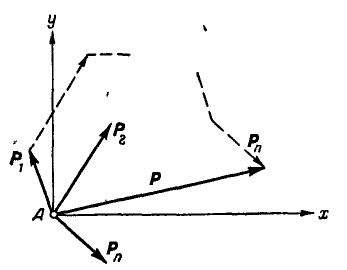
Рис. 22.

Обозначая равнодействующую сил через Р, можем написать:

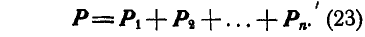
Проектируя равнодействующую и составляющие на координатные оси, проведенные через точку А, по формуле (3) имеем:

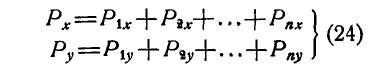
Величину равнодействующей находим по формуле (7):

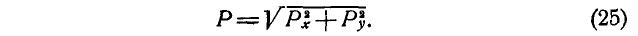
Направление равнодействующей определяем по формулам (6):

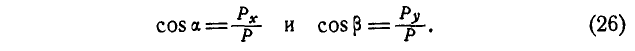
Может оказаться, что при построении многоугольника сил конец последней силы совпадет с началом первой; в этом случае многоугольник сил получается замкнутым, равнодействующая сила равна нулю и силы находятся в равновесии. Таким образом, геометрическое условие равновесия сил, приложенных к точке, заключается в том, что многоугольник этих сил должен быть замкнут.        

В этом случае Р=0, а поэтому и 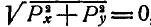   , а это может быть при условии, когда 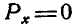и 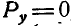, что возможно, если:

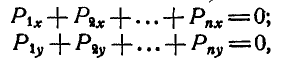
или сокращенно:

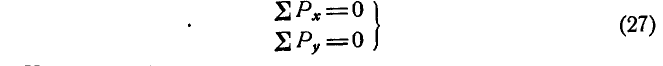
Уравнения (27) называются уравнениями равновесия сил, приложенных к точке, и выражают аналитические условия равновесия этих сил.

Рассмотрим равновесие трех сил 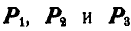, действующих на тело (рис. 23).

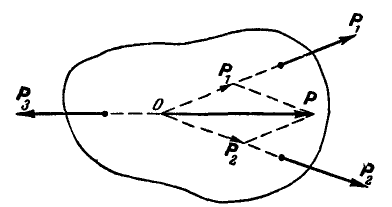
Рис. 23.

Пусть в точке О пересекаются линии действия любых двух сил, например 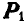и 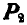, тогда эти силы можно перенести в точку О и по правилу параллелограмма заменить одной силой Р.

Теперь на тело уже действуют две силы Р и А, равновесие которых по аксиоме 2 возможно, если они будут направлены по одной прямой.

Отсюда заключаем, что три силы, действующие на тело, и расположенные в одной плоскости, могут находиться в равновесии только тогда, когда их линии действия пересекаются в одной точке.

• Заказать решение задач по теоретической механике

Задача 1.

К точке В шарнирного кронштейна АВС (рис. 24, а) подвешен груз Q = 100 кГ. Определить усилия 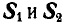в стержнях ВА и ВС.

Решение. Для определения усилия 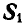в стержне ВА, который является связью для точки В, освободимся от связи и введем реакцию стержня, которая, согласно аксиоме 6, будет равна и прямо цретивоположна искомому усилию 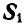(рис. 24, б). Теперь точка В находится в равновесии под действием двух сил 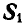и 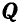и имеет возможность двигаться по дуге окружности радиуса ВС (рис. 24, б). Поэтому равновесие точки В возможно будет только тогда, когда равнодействующая этих двух сил 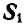и 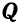пойдет по направлению оси стержня ВС. Но это равносильно тому, что проекция ее на направление 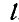, перпендикулярное к стержню ВС, будет равна нулю, или, что то же, сумма проекций составляющих на это направление равна нулю: 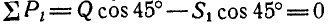, откуда .

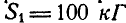Для нахождения усилия 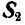 в стержне ВС поступаем аналогично. Устраняем связь ВС и взамен ее вводим реакцию 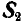(рис. 24, в); тогда точка В должна находиться в равновесии под действием двух сил 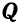и 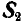. Проектируя эти силы на направление у возможного движения точки В, получим условие равновесия точки В в виде: 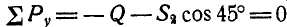, откуда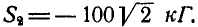

При решении этой задачи можно было бы освободиться одновременно от обеих связей ВА и ВС, вводя взамен их реакции связе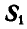й и 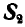(рис. 24,г).

Тогда для свободной точки В можно написать два уравнения равновесия (27) в виде:

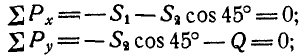
отсюда находим, что 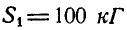и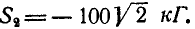

Знак минус у 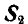указывает на то, что направление реакции нами выбрано неправильно и это направление следует изменить на обратное. На рисунке 24, д дано правильное направление стрелок реакций связей.

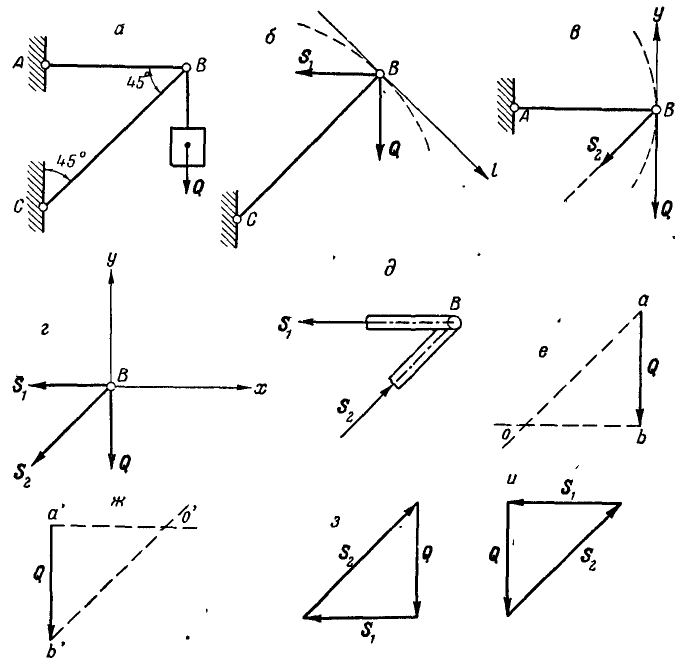
Рис. 24.

При неподвижной точке В реакция направленная от узла, будет растягивать стержень, а реакция 58, направленная к узлу, будет сжимать стержень, что ясно видно из чертежа.

Решим теперь эту задачу геометрическим способом. Все силы, заданные и реактивные, действующие на точку В, взаимно уравновешиваются, а поэтому многоугольник этих сил должен быть замкнут. На этом основании проводим вектор, равный силе 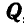, и из начала и конца этого вектора проводим направления, параллельные линиям действия реакций связей ВА и ВС (рис. 24, е или 24, ж); в пересечении этих направлений получаем точку О или О'.

Так как многоугольник сил, действующих на точку В, должен быть замкнут, то стрелки всех сил в полученном многоугольнике сил, в нашем случае - треугольнике (рис. 24, е или 24, ж), должны быть расположены в одном направлении. Исходя из заданного направления силы , получим правильное направление стрелок реактивных сил 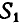 и 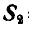(рис. 24, з или 24, м).

Выбрав один из полученных треугольников сил, замечаем, что сила 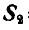, перенесенная параллельно самой себе на стержень 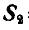(рис. 24, а или 24, д), будет направлена к узлу В, следовательно, стержень ВС — сжат, а сила 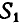направленная от узла В, будет растягивать стержень ВА. Из полученного треугольника сил (рис. 24, з или 24, и) имеем:

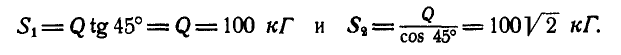
При решении дальнейших задач аналитическим способом стрелки неизвестных реакций стержней будём направлять всегда от рассматриваемого нами узла; тогда знак минус у модуля реакции какого-либо стержня будет указывать на то, что рассматриваемый нами стержень сжат.

Задача 2.

Определить усилия в стержнях АВ и ВС при действии в шарнире В силы Q=100 кГ, если АВ = ВС =5 м, BD = 0,5 м и шарниры А и С расположены на одной горизонтали (рис. 25, а).

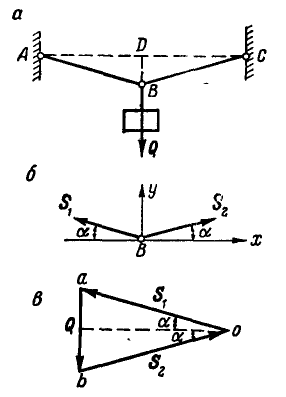
Рис. 25.

Решение. Решим сначала задачу аналитическим способом, для чего рассмотрим равновесие точки В, находящейся под действием трех сил: заданной силы 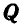и реакций связе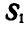й и 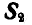(рис. 25, б).

Применяя уравнения равновесия (27), имеем:

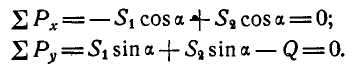
Из первого уравнения находим: 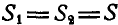; тогда второе уравнение примет вид: 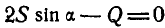, откуда 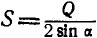. Из  ΔABD  имеем: 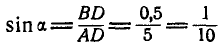, поэтому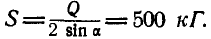 

Знак плюс у S указывает на то, что оба стержня ВА и ВС растянуты.

Для решения этой задачи геометрическим способом, построим треугольник равновесия 0ab (рис. 25,в), из которого сразу находим правильное направление реакци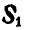и и 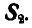. Далее 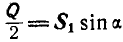, или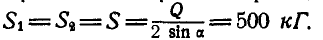

Задача 3.

Однородный цилиндр (рис. 26,а) весом 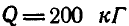опирается на гладкую плоскость, наклоненную под 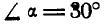к горизонту и удерживается в равновесии горизонтальным канатом 0С. К оси цилиндра О приложена сила Р=400 кГ, направленная параллельно плоскости. Найти реакцию N плоскости и натяжение Т каната ОС.

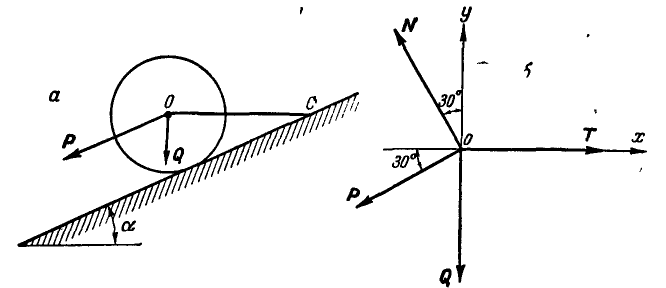
Рис. 26.

Решение. Решим задачу аналитическим способом. Освободившись от связей (рис. 26,6) и составляя для точки О уравнения равновесия (27), имеем:

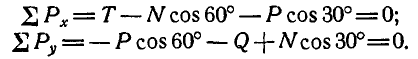
Подставляя вместо Р и Q их значения и решая полученные уравнения, находим неизвестные силы:

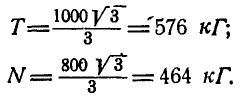
Задача 4.

Жесткое колено ABCD (рис. 27,а), могущее вращаться вокруг шарнира В, опирается в точке D на гладкий уступ. Пренебрегая весом колена, определить реакции связей в точках В и D, если в точке А колена приложена сила Р=100 кГ.

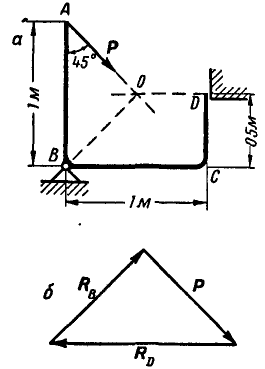
Рис. 27.

Решение. Так как колено находится в равновесии, то три силы, действующие в точках А, В и D, должны пересекаться в одной точке. Продолжаем линию действия силы Р  и реакции в точке D, направленной перпендикулярно к плоскости уступа, до взаимного пересечения в точке О; тогда линия действия реакции шарнира В пройдет обязательно через точку О. На рисунке 27, б дано построение треугольника равновесия трех сил 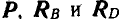, из которого следует, что 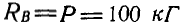и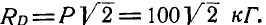

Задача 5.

При подъеме плуга на стоянке (рис. 30) поворачивают коленчатый рычаг АВС, вращая рукоятку силой Р. Какова при этом должна быть величина силы Р, если вес части плуга, передающейся на коленчатый рычаг, вращающийся вокруг шарнира В, равен Q = 30 кГ, длина рукоятки АВ = 0,6 м и радиус колеса плуга г = 0,25 м.

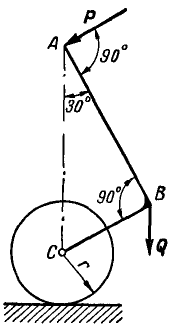
Рис. 30.

Решение. Строим для сил, приложенных к коленчатому рычагу, треугольник равновесия. Из подобия треугольника равновесия и соответствующего треугольника на чертеже находим силу Р.

Ответ: Р = 11 кГ.