Синтез электрических цепей

Содержание:

Синтез электрических цепей:

Кроме подробно рассмотренного анализа процессов в различных электрических цепях, весьма важной является обратная задача — синтез, т. е. построение такой электрической цепи, процессы в которой протекают заданным образом. Примером синтеза является построение схемы и определение параметров двухполюсника с заданным комплексным сопротивлением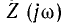

Необходимо подчеркнуть, что задачи синтеза имеют неоднозначные решения, так как заданную характеристику может иметь ряд цепей, из которых надо выбрать простейшую. Некоторые задачи синтеза неразрешимы, потому что не все задаваемые характеристики могут быть осуществлены сочетанием элементов типа г, L и С.

В литературе, посвященной ряду областей техники, сложная теория синтеза рассматривается подробно. Она состоит из предварительного анализа возможности решения поставленной задачи по виду заданной функции Z (р) или К (р) и в положительном случае — из обоснования ряда методов ее реализации в виде электрических цепей.

Далее рассматривается только синтез двухполюсников по заданной функции Z (р) путем представления ее в виде цепной дроби или суммы простых дробей, дается понятие о синтезе четырехполюсников на примере дифференцирующих и интегрирующих цепей, а также приводятся некоторые соображения о синтезе нелинейных цепей.

Синтез двухполюсников методом цепных дробей

Если искомый двухполюсник представить в виде цепной схемы его операторное сопротивление может быть подсчитано методом преобразования и записано в виде цепной дроби. Так, для схемы вида рис. 19.1, состоящей из чередующихся «продольных» ветвей Z_к (р) и «поперечных» ветвей Y_k (р), операторное сопротивление

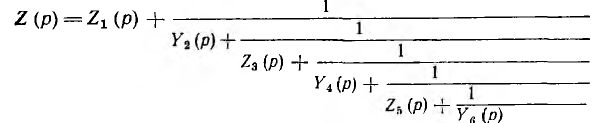
Если читать это выражение снизу вверх, оно наглядно представляв схему цепи, ее ветви и весь ход преобразования.

Отсюда вытекает возможность синтезировать цепь по заданному операторному сопротивлению

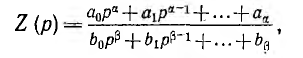
если привести его к виду цепной дроби путем постепенного деления числителя на знаменатель. Частное от деления первого члена числителя на первый член знаменателя равно 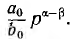Поэтому первый член частного физически осуществим, если степени полиномов числителя 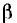и знаменателя f$ равны или отличаются не больше, чем на единицу, так как только тогда этот член получает вид А или А_р, или 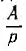, где А — постоянная, т. е. представляет собой осуществимое операторное сопротивление — активное г или индуктивное Lp, или емкостное 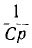или соответствующие проводимости.

Пусть, например, операторное сопротивление синтезируемой цепи

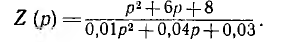
Здесь степени полиномов в числителе и знаменателе равны. Ход преобразования Z (р) имеет вид:

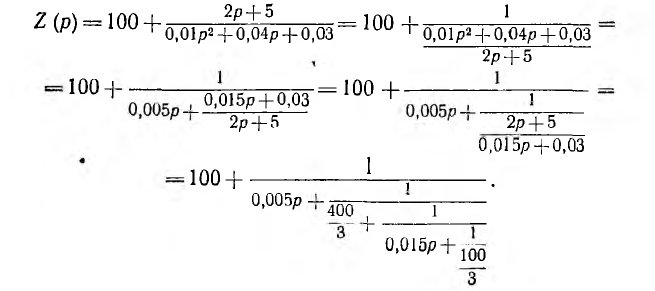
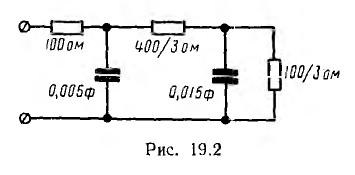
При сопоставлении этой цепной дроби с цепной дробью Z (р) для схемы рис. 19.1 видно, что 100, -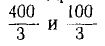 являются активными сопротивлениями; 0,005 р и 0,015 р — операторными емкостными проводимостями, а цепь имеет схему рис. 19.2 с указанными на ней значениями параметров.

Вторым примером может служить синтез цепи, в выражении операторного сопротивления которой степени полиномов числителя и знаменателя отличаются на единицу:

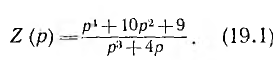
Важно отметить, что вид Z (р) в данном частном случае, когда показатели степени р в полиномах числителя и знаменателя отличаются на единицу и снижаются сразу на две, указывает на чисто реактивный характер цепи. В этом можно убедиться, подставив 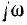вместо р и получив мнимое значение Z (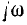). Из преобразования

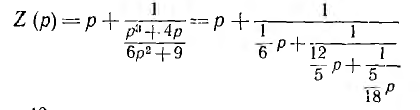
видно, что р и 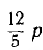являются операторными индуктивными сопротивлениями, -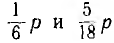—емкостными проводимостями, а цепь имеет схему, представленную на рис. 19.3, а с указанными на ней значениями параметров.

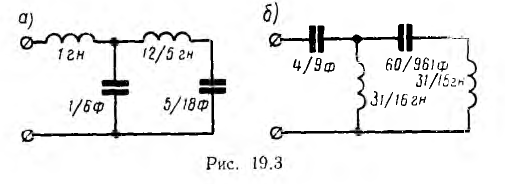
Если расположить полиномы числителя и знаменателя не по нисходящим, а по восходящим степеням р, ход преобразования в цепную дробь получит вид:

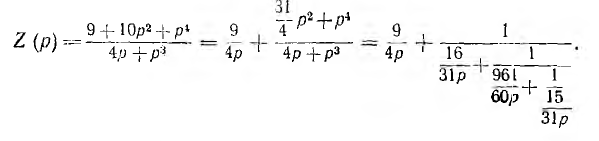
„ 9 961

Отсюда видно, что 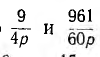являются операторными емкостными сопротивлениями, 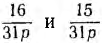— индуктивными проводимостями, а цепь имеет схему, представленную на рис. 19.3, б с указанными значениями параметров.

Таким образом, обе схемы рис. 19.3, а и б решают задачу синтез цепи с заданным Z (р), что подтверждает упомянутую выше неоднозначность решения задач синтеза.

Синтез двухполюсников методом простых дробей

В этом методе синтезируемая цепь представляется в виде последовательного соединения элементарных участков. Тогда ее операторное сопротивление Z (р) будет равно сумме их операторных сопротивлений.

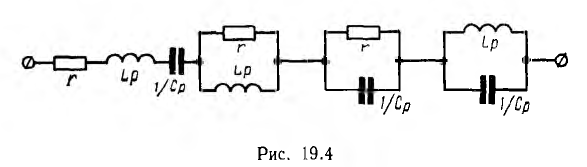
Этими элементами цепи, изображенной на рис. 19.4, являются участки с активным сопротивлением г, с индуктивным Lp и с емкостным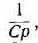а также участки с параллельным соединением г и L, г и С, l и с. Их операторные сопротивления, соответственно, равны:

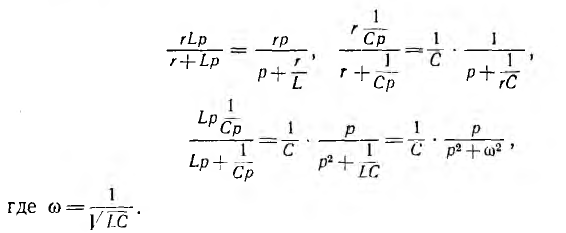
Таким образом, синтезируемое сопротивление Z (р), заданное в виде частного двух полиномов, должно быть преобразовано в сумму следующих простых дробей:

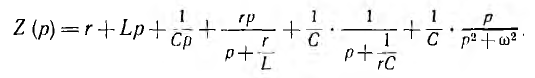
Некоторые члены суммы могут отсутствовать, а некоторые повторяться с другими параметрами.

Далее этот метод синтеза рассматривается на примере. Пусть законное операторное сопротивление

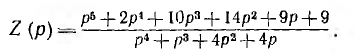
Так как степень числителя на единицу больше степени знаменателя, сначала из Z (р) выделяется составляющая, пропорциональная первой степени р. Для этого числитель делится на знаменатель, как это делалось в методе цепных дробей:

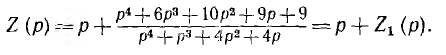
Выделенная первая составляющая есть операторное индуктивное сопротивление Lp, т. е. L = 1 гн. Теперь к оставшейся правой части Z₁ (р) может быть применено разложение на простые дроби, обоснованное  при выводе теоремы разложения:

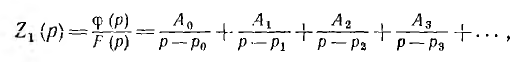
где р₀, р₁, р₂, р₃ — корни уравнения F (р) = 0. В рассматриваемом примере

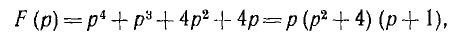
т. е. уравнение F (р) = О имеет корни р₀ = 0, 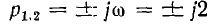и р₃ = — 1.

Корень Р_о = 0 позволяет выделить простую дробь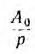, причем

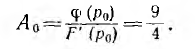
Следовательно, вторая составляющая равна 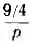, т. е. представляет собой емкость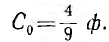

Можно показать, что числители простых дробей, соответствующих мнимым корням 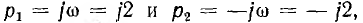вещественны и равны между собой, т. е. 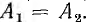. Тогда сумма этих дробей

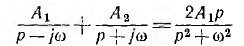
дает третью простую составляющую. Из сопоставления с приведенными выше операторными сопротивлениями элементарных участков видно, что она представляет собой операторное сопротивление параллельного соединения 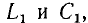равное

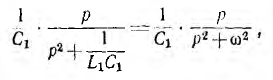
где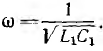

Следовательно

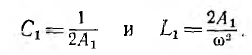
Числители соответствующих простых дробей в общем виде и в расматриваемом примере после подстановки в выражение для Z₁ значения 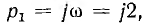а также третья составляющая, равны

откуда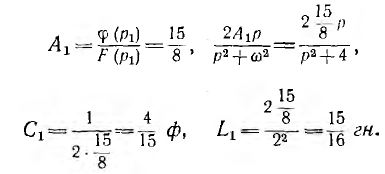

Остается синтезировать Z₂ (р), определяемое вычитанием из Z₁ (р) найденных второй и третьей составляющих:

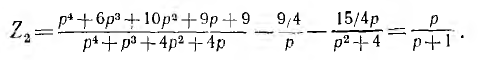
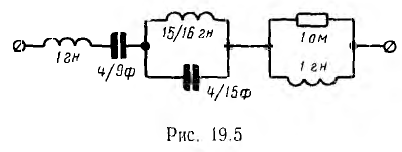
Из сравнения этой дроби с приведенным выше выражением операторных сопротивлений видно, что она представляет параллельное соединение г и L, причем г = 1 ом, a L = |r| = 1 гн, т. е. является четвертой последней составляющей Z (р). В результате схема синтезируемого двухполюсника получает вид, показанный на рис. 19.5. Операторное сопротивление схемы, состоящей из первых трех составляющих цепи рис. 19.5,

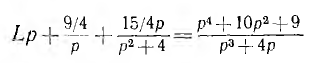
равно операторному сопротивлению Z (р) по формуле 19.1, синтезированному ранее методом цепных дробей. Таким образом, эта схема, отдельно показанная на рис. 19.6, а, является третьим вариантом синтеза Z (р), но полученным методом простых дробей.

Во всех предыдущих примерах рассматривался синтез цепи по заданному ее операторному сопротивлению Z (р), однако синтез может осуществляться и по проводимости этой цепи 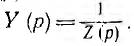. При этом простые составляющие А, Ар и 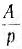, будут не последовательно соединенными сопротивлениями, а параллельно включенными проводимостями, составляющая же 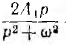не параллельно, а последовательно соединенными L и С.

Далее в качестве примера синтезируется методом простых дробей цепь с тем же Z (р), что и  (см. выражение 19.1), но по ее заданной операторной проводимости

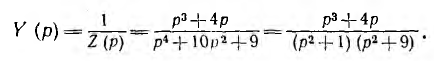
Так как степень числителя меньше степени знаменателя, а знаме-натель не имеет корня р₀ = 0, составляющие, пропорциональные р и 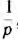, будут отсутствовать. Знаменатель У (р) имеет две пары мнимых корней 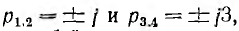, следовательно, У (р) является суммой простых дробей

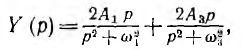
где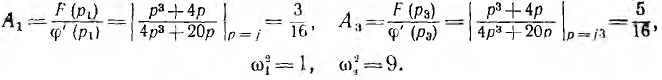

Так как проводимость цепи с последовательным соединением L и С равна

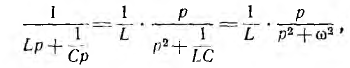
параметры обеих ветвей У (р) будут:

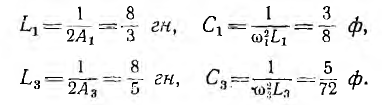
Следовательно, синтезируемая цепь имеет вид, показанный на рис. 19.6, б, — это четвертый вариант синтеза цепи с тем же заданным Z (р).

Синтез цепи можно вести также комбинированным методом. Например, выделив первый элементарный участок методом простых дробей, остаток можно синтезировать дальше методом цепных дробей, причем полиномы числителя и знаменателя дроби, представляющей собой 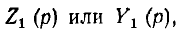можно расположить по нисходящим или по восходящим степеням и т. п. Все эти различные ходы расчета могут дать новые варианты синтезируемой цепи. При реализации синтезируемой иепи из всех вариантов выбирается оптимальным — схема, состоящая из наиболее просто технически осуществимых г, L и С.

Дифференцирующие и интегрирующие цепи

В качестве простейшего примера синтеза четырехполюсников рассматривается задача создания дифференцирующих и интегрирующих цепей, напряжение 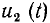на выходе которых пропорционально производной или интегралу напряжения u₁ (t) на входе. Для упрощения задачи можно пренебречь выходным током по сравнению с током на входе, т. е. рассмотреть режим холостого хода синтезируемого четырехполюсника.

Напряжение и ток индуктивности и емкости связаны известными зависимостями которые и могут быть использованы для решения поставленной задачи. В большинстве случаев в качестве реактивных элементов применяются конденсаторы, так как катушки индуктивности обладают большими потерями, а также межвитковой емкостью.

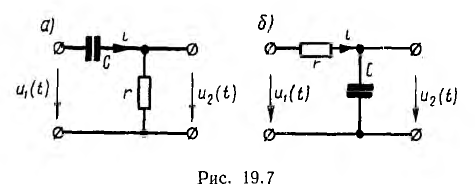
Выходной величиной дифференцирующей цепи должно быть напряжение, а не ток 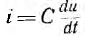, поэтому приходится последовательно с емкостью С включить сопротивление r, кривая напряжения на котором повторяет форму кривой тока. С этого сопротивления и снимается напряжение выхода u₂ (г) = ri (рис. 19.7, а). Величина г должна быть относительно малой, чтобы напряжение u₂ (t) было пренебрежимо мало по сравнению с напряжением u_с (t) на конденсаторе. Тогда

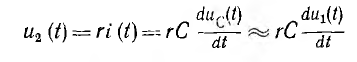
или при нулевых начальных условиях

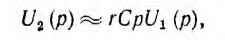
г. е. рассматриваемый четырехполюсник при сделанных допущениях шляется дифференцирующей цепью. Его передаточная функция

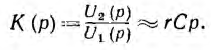
В интегрирующей цепи необходимо последовательно : емкостью, с которой снимается напряжение выхода u₂ = u_с, включить сопротивление г (рис. 19.7, б). Величина г должна быть относительно большой, чтобы напряжение u_с на конденсаторе было пренебрежимо мало по сравнению с напряжением ri на сопротивлении. Тогда

или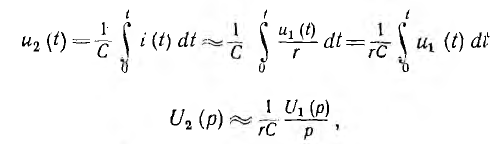

т. е. рассматриваемый четырехполюсник при сделанных допущениях является интегрирующей цепью. Его передаточная функция

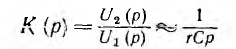
обратна передаточной функции рассмотренной дифференцирующей цепи. Следует отметить, что в обеих цепях напряжения u₂ (t) на выходе получаются значительно меньше напряжений u₁ (t) на входе. Этот недостаток устраняется применением на выходе усилителей.

О синтезе нелинейной цепи

В задачу синтеза нелинейной цепи обычно входит подбор нелинейного элемента, обладающего необходимой характеристикой, и построение цепи, в которой эта характеристика может быть использована. Пусть, например, при синусоидальном входном напряжении 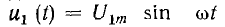четырехполюсника на его выходе требуется получить пикообразное периодическое напряжение u₂ (t). Известно, что при синусоидальном напряжении ток катушки с насыщаемым стальным сердечником имеет пикообразную форму (см. рис. 14.1). Чтобы получить пикообразное напряжение выхода, его надо снимать с сопротивления г, включенного последовательно с катушкой (рис. 19.8), причем это сопротивление должно быть мало по сравнению с эквивалентным сопротивлением катушки.

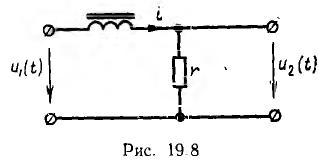
Величина амплитуды тока цепи должна обеспечить насыщение стального сердечника. Из соотношения сопротивлений видно, что выходное напряжение будет значительно меньше входного.

Приведенные примеры дают лишь общее представление о синтезe электрических цепей, отнюдь не исчерпывая всего содержания этой нового и сложного раздела теории цепей.