Задание №20. Для разумного планирования и организации работы ремонтных мастерских специальной техники оказалось необходимым изучить

		Теория вероятностей
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16394
		Прошла проверку преподавателем МГУ
		245 руб.

Задание №20. Для разумного планирования и организации работы ремонтных мастерских специальной техники оказалось необходимым изучить длительность ремонтных операций, производимых мастерскими. Получены результаты (сгруппированные по интервалам) соответствующего статистического обследования (фиксированы длительности операций в 100 случаях): [𝑥𝑖 , 𝑥𝑖+1) [0; 3) [3; 6) [6; 9) [9; 12) [12; 15) [15; 18) [18; 21) [21; 24) 𝑛𝑖 27 19 16 13 11 8 4 2 Требуется: 1) построить гистограмму частостей; 2) найти числовые характеристики выборки (𝑥̅𝐵, 𝑆, 𝐴̅, 𝐸̅); 3) по виду гистограммы и значениям числовых характеристик выдвинуть гипотезу о законе распределения случайной величины 𝑋 – длительности ремонтных операций, оценить параметры теоретического закона и записать его вид; 4) проверить основную гипотезу о законе распределения 𝑋 по критерию согласия Пирсона (уровень значимости выбрать самостоятельно).

Решение

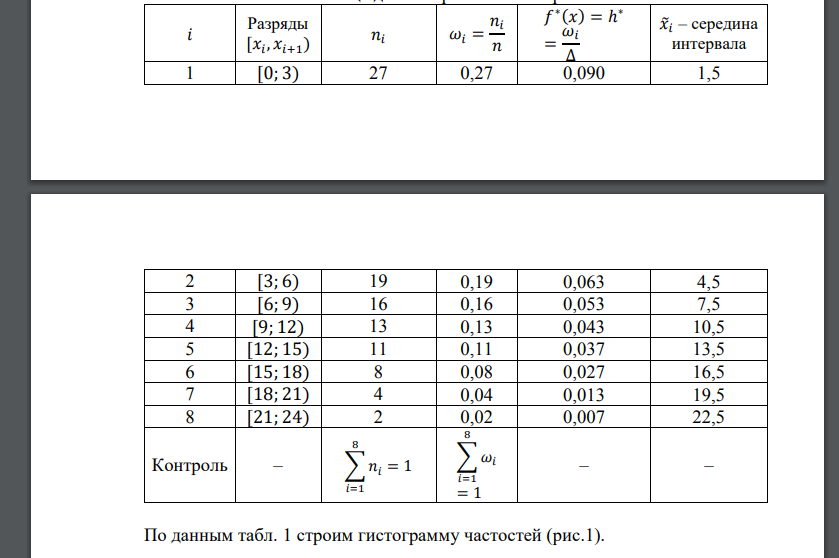
1) Для построения гистограммы строим вспомогательную табл. 1: Таблица 1 Расчетная таблица для построения гистограммы частостей 𝑖 Разряды– середина интервала Контроль –  По данным табл. 1 строим гистограмму частостей (рис.1). Рис.1. Гистограмма частостей 2) Находим числовые характеристики выборки: 3) Положительный коэффициент асимметрии говорит о правосторонней асимметрии распределения. Учитывая вид гистограммы и близость статистического среднего 𝑥̅𝐵 и выборочного среднего квадратического отклонения 𝜎в по своим значениям, выдвигаем основную гипотезу в пользу показательного закона распределения, функция плотности которого имеет вид:  Найдем оценку 𝜆 ∗ параметра 𝜆 показательного закона распределения. Выборочное среднее  – несмещенная и состоятельная оценка математического ожидания. Используя метод моментов, имеем  Заменяя 𝜆 оценкой 𝜆 ∗ , получаем теоретический закон распределения: Критерий Пирсона применяется при условии, что все группы ряда включают частоты не меньшие . Если частота группы ряда менее 5, то эту группу следует объединить с соседней. В данном случае объединим два последних интервала.Вероятность попадания случайной величины в каждый интервал для показательного распределения равна:  Вероятности попадания случайной величины 𝑋 в каждый интервал: Найдем теоретические частоты и вычислим значения Результаты запишем в таблицу Интервал Получили . Число степеней свободы . Зададим уровень значимости 𝛼 = 0,05, тогда по таблице значений 𝜒 2 находим  Так как , то гипотеза о распределении случайной величины 𝑋 по показательному закону при заданном уровне значимости принимается.