В табл. приведены значения констант скоростей k1 и k2 реакции при двух различных температурах T1 и T2. Вычислите

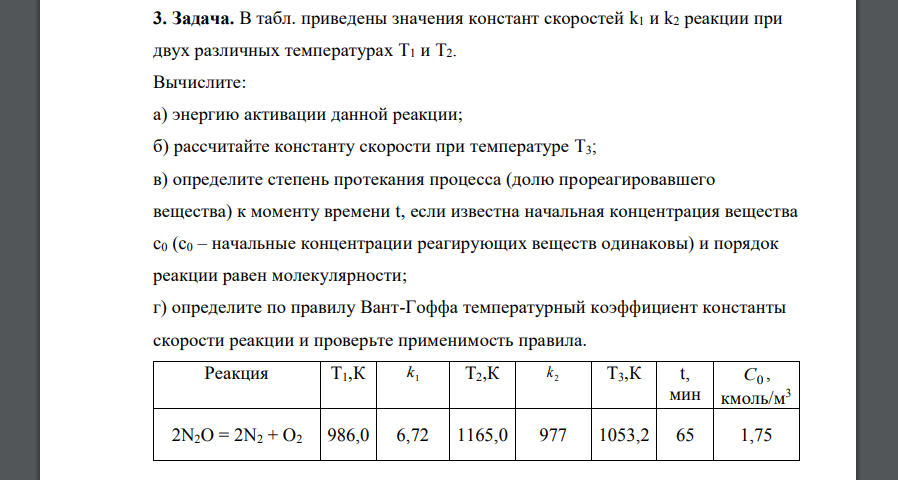
В табл. приведены значения констант скоростей k1 и k2 реакции при двух различных температурах T1 и T2. Вычислите: а) энергию активации данной реакции; б) рассчитайте константу скорости при температуре T3; в) определите степень протекания процесса (долю прореагировавшего вещества) к моменту времени t, если известна начальная концентрация вещества c0 (c0 – начальные концентрации реагирующих веществ одинаковы) и порядок реакции равен молекулярности; г) определите по правилу Вант-Гоффа температурный коэффициент константы скорости реакции и проверьте применимость правила. Реакция Т1,К 1 k Т2,К 2 k Т3,К t, мин С0 , кмоль/м3 2N2O = 2N2 + O2 986,0 6,72 1165,0 977 1053,2 65 1,75

Решение.

 для нахождения энергии активации воспользуемся интегральной формой уравнения Аррениуса:  для нахождения k3 при Т3 воспользуемся той же формулой уравнения Аррениуса:  в) Константа скорости реакции второго порядка описывается выражением  Степень протекания реакции равна  г) Для определения температурного коэффициента скорости воспользуемся математическим выражением правило Вант – Гоффа:  Проверим применимость правила Вант-Гоффа. Рассчитаем  Получили близкое значение к рассчитанному по уравнению Аррениуса, поэтому правило Вант-Гоффа применимо к данной реакции в заданных условиях