В результате выборочного обследования российских автомобилей, которые обслуживаются в автосервисе по гарантии, по схеме собственно-случайной

		Математическая статистика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16472
		Прошла проверку преподавателем МГУ
		245 руб.

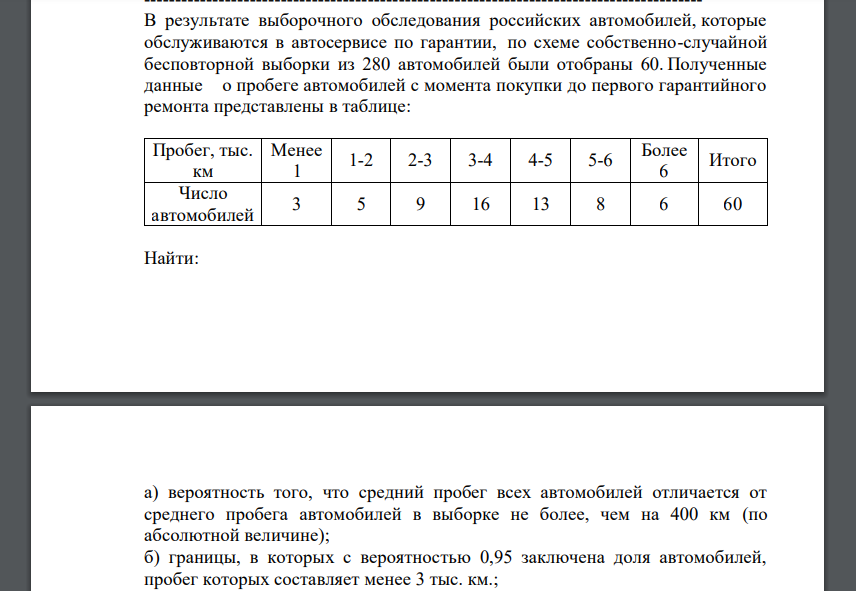
В результате выборочного обследования российских автомобилей, которые обслуживаются в автосервисе по гарантии, по схеме собственно-случайной бесповторной выборки из 280 автомобилей были отобраны 60. Полученные данные о пробеге автомобилей с момента покупки до первого гарантийного ремонта представлены в таблице: Пробег, тыс. км Менее 1 1-2 2-3 3-4 4-5 5-6 Более 6 Итого Число автомобилей 3 5 9 16 13 8 6 60 Найти: а) вероятность того, что средний пробег всех автомобилей отличается от среднего пробега автомобилей в выборке не более, чем на 400 км (по абсолютной величине); б) границы, в которых с вероятностью 0,95 заключена доля автомобилей, пробег которых составляет менее 3 тыс. км.; в) объем бесповторной выборки, при котором те же границы для доли (см. п.б)), можно гарантировать с вероятностью 0,9876.

Решение

Преобразуем данную таблицу в таблицу частот, выбрав середины интервалов за значения пробега. Значение пробега обозначим через 𝑥𝑖 ; число автомобилей обозначим через 𝑛𝑖 :  Вычислим числовые характеристики: Выборочную среднюю 𝑥̅:   Выборочную дисперсию а) Найдем вероятность того, что средний пробег всех автомобилей отличается от среднего пробега автомобилей в выборке не более, чем на 400 км (по абсолютной величине). Средняя квадратическая ошибка при оценке генеральной средней для собственно-случайной бесповторной выборки достаточно большого объема находим по формуле: где 𝜎 2 − выброчная дисперсия, 𝑛 – объем выборки, 𝑁 – объем генеральной совокупности Доверительная вероятность (надежность) при оценке генеральной средней для собственно случайной бесповторной выборки достаточно большого объема, определяется по формуле:  Тогда при ∆= 400 км = 0,4 тыс. км. получим:  б) Найдем границы, в которых с вероятностью 0,95 заключена доля автомобилей, пробег которых составляет менее 3 тыс. км. Выборочная доля автомобилей, пробег которых составляет менее 3 тыс. км., равна  Средняя квадратическая ошибка собственно-случайной бесповторной выборки при оценке генеральной доли, находится по формуле: