В некотором городе по схеме собственно случайной бесповторной выборки было обследовано 180 магазинов розничной торговли из 2500 с целью

		Математическая статистика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16423
		Прошла проверку преподавателем МГУ
		245 руб.

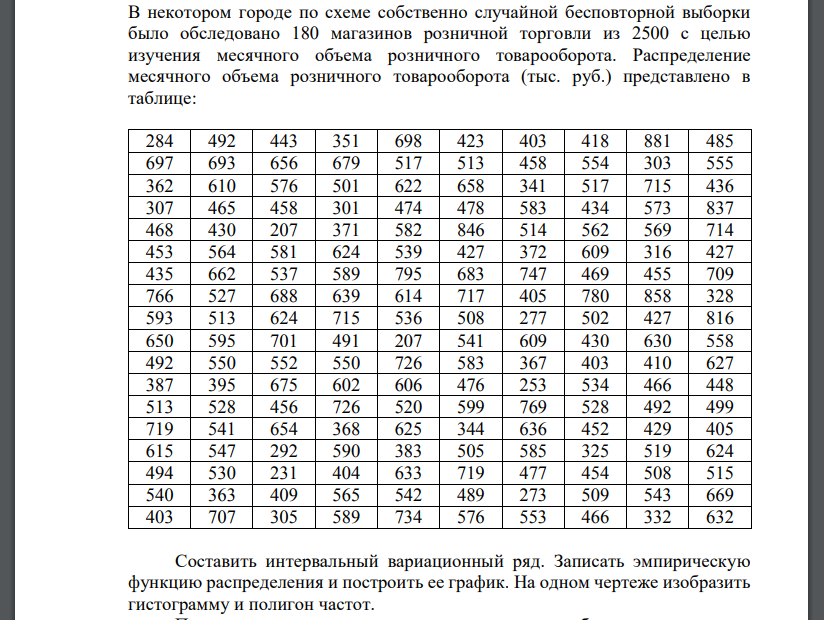
В некотором городе по схеме собственно случайной бесповторной выборки было обследовано 180 магазинов розничной торговли из 2500 с целью изучения месячного объема розничного товарооборота. Распределение месячного объема розничного товарооборота (тыс. руб.) представлено в таблице:

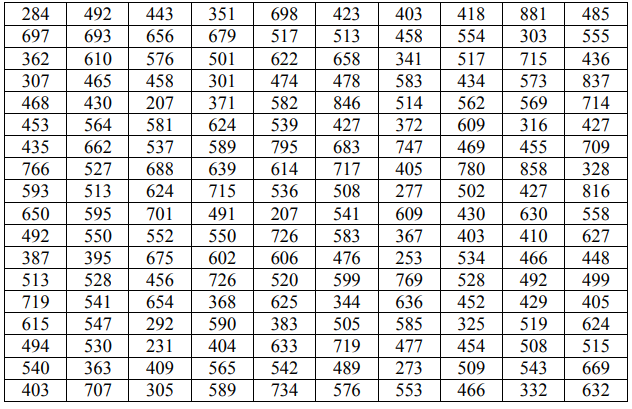
Составить интервальный вариационный ряд. Записать эмпирическую функцию распределения и построить ее график. На одном чертеже изобразить гистограмму и полигон частот. По сгруппированным данным вычислить выборочные числовые характеристики: среднее арифметическое, исправленную выборочную дисперсию, среднее квадратичное отклонение, коэффициент вариации, асимметрию, эксцесс, моду и медиану. Найти: а) границы, в которых с вероятностью 0,96 будет заключен месячный товарооборот всех торговых предприятий города; б) вероятность того, что доля всех торговых предприятий города, месячный товарооборот которых не превышает 500 тыс. руб., отличается от доли предприятий, полученной по выборке не более, чем на 0,05 (по абсолютной величине); в) объем бесповторной выборки, при котором те же границы для среднего месячного товарооборота всех торговых предприятий города, полученные в п. а) можно гарантировать с вероятностью 0,98.

Решение

Построим выборку в порядке возрастания: Найдем размах выборки Число интервалов 𝑁, на которые следует разбить интервал значений признака, найдём по формуле Стерджесса:  где n − объём выборки, то есть число единиц наблюдения. В данном случае 𝑛 = 180. Получим:  Рассчитаем шаг (длину частичного интервала) ℎ по формуле:  Округление шага производится, как правило, в большую сторону. Таким образом, принимаем. За начало первого интервала принимаем такое значение из интервала чтобы середина полученного интервала оказалась удобным для расчетов числом. В нашем случае за нижнюю границу интервала возьмём 206. Подсчитаем частоту 𝑛𝑖 каждого интервала, то есть число вариант, попавших в этот интервал. Варианты, совпадающие с границами частичных интервалов, включают в правый интервал. Относительные частоты (частости) 𝑤𝑖 и плотность относительной частоты 𝑝̃𝑖 определим по формулам: