Автор Анна Евкова
Преподаватель который помогает студентам и школьникам в учёбе.

Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром

Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром Физика
Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром Решение задачи
Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром
Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром Выполнен, номер заказа №16485
Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром Прошла проверку преподавателем МГУ
Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром  245 руб. 

Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром

Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!

Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром

Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):

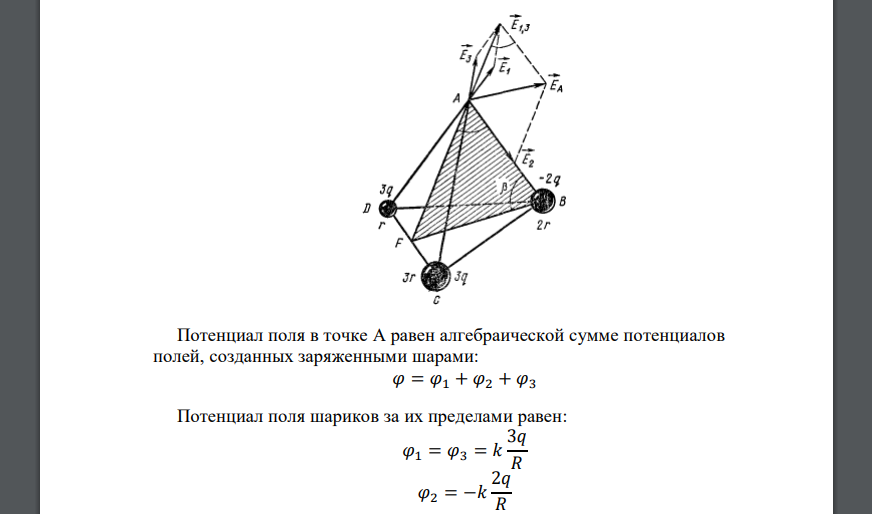
Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром R» г. Определить потенциал поля в четвертой вершине тетраэдра.

Решение:

Потенциал поля в точке А равен алгебраической сумме потенциалов полей, созданных заряженными шарами:  Потенциал поля шариков за их пределами равен:  Тогда:  Потенциал поля в центре шариков равен потенциалу на их поверхности. Последний складывается из потенциала собственного поля шарика и потенциалов полей двух других шариков. Учитывая, что  а также знаки зарядов на шариках, мы можем записать:  Ответ:

Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром

Три проводящих шарика радиусами г, 2r, Зr, на которых находятся заряды 3q, ~3q. 2q, расположены в вершинах тетраэдра с ребром