С.в распределена по экспоненциальному закону с параметром 3. Найти плотность распределения и математическое ожидание случайной величины 𝑌 = 𝑋 2 + 1
 |
 |
Математический анализ |
 |
 |
Решение задачи |
 |
 |
|
 |
 |
Выполнен, номер заказа №16309 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
|
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл! |
|
Закажите у меня новую работу, просто написав мне в чат! |
С.в распределена по экспоненциальному закону с параметром 3. Найти плотность распределения и математическое ожидание случайной величины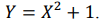 
Решение
Функция плотности распределения вероятности 𝑓(𝑥) случайной величины 𝑋, имеющей показательное распределение с параметром 3, имеет вид: Построим схематично график функции для 𝑥 в интервале Так как функция монотонна на участке то применяется формула: где 𝜓 − функция, обратная функции 𝜑. Определим диапазон значений 𝑌 по графику: В зависимости от числа обратных функций 𝑘 выделим следующие интервалы для 𝑌: В интервалах обратные функции не существуют, следовательно, плотность вероятности Решение задачи оформим в виде двух столбцов: в левом будут помещены обозначения функции, принятые в общем решении задачи, в правом – конкретные функции, соответствующие данному примеру: Тогда в интервале Таким образом, плотность распределения вероятности величины 𝑌 равна: Математическое ожидание случайной величины 𝑈 равно: Ответ: 𝑚𝑌 = 1,222
Похожие готовые решения по математическому анализу:
- Случайная величина 𝑋 распределена с плотностью 𝑝𝑋 (𝑥) = 𝑎𝑥, 𝑥 ∈ [2; 4]. Найти плотность распределения и м.о. с.в. 𝑌 = √𝑋 − 2
- Непрерывная случайная величина 𝑋 имеет плотность 𝑝(𝑥) = 1 − 𝑥/2, 𝑥 ∈ [0; 2] Найти плотность распределения и математическое ожидание с.в. 𝑌 = √𝑋 + 1
- Случайная величина 𝑋 распределена по показательному закону с параметром 𝜆. Найти плотность распределения вероятностей и математическое ожидание
- Случайная величина 𝑋 распределена по непрерывному закону с плотностью распределения 𝑝(𝑥) = 𝑐|𝑥|, −1 ≤ 𝑥 ≤ 1. Найти плотность распределения и математическое ожидание
- Дана плотность распределения некоторой случайной величины: 𝑓(𝑥) = { 0, 𝑥 < 0 𝐶𝑥 16 , 0 ≤ 𝑥 < 1 0, 𝑥 ≥ 1 Найдите значение константы 𝐶, функцию распределения, постройте её график
- Дана плотность распределения некоторой случайной величины: 𝑓(𝑥) = { 0, 𝑥 < 0 𝐶𝑥 17 , 0 ≤ 𝑥 < 1 0, 𝑥 ≥ 1 Найдите значение константы 𝐶, функцию распределения
- Дана плотность распределения некоторой случайной величины: 𝑓(𝑥) = { 0, 𝑥 < 0 𝐶𝑥 18 , 0 ≤ 𝑥 < 1 0, 𝑥 ≥ 1 Найдите значение константы 𝐶, функцию распределения, постройте её график
- Дана плотность распределения некоторой случайной величины: 𝑓(𝑥) = { 0, 𝑥 < 0 𝐶𝑥 20 , 0 ≤ 𝑥 < 1 0, 𝑥 ≥ 1 Найдите значение константы 𝐶, функцию распределения
- Для изучения потока посетителей в систему массового обслуживания (например, магазин, сбербанк и т.д.) был произведен хронометраж интервалов
- В пирамиде 8 винтовок, из которых 5 снабжены оптическим прицелом. Вероятность поразить мишень из винтовки с оптическим
- Для изучения потока посетителей в систему массового обслуживания (например, магазин, сбербанк и т.д.) был произведен хронометраж интервалов между
- При каждом выстреле, независимо от остальных выстрелов, первый стрелок попадает в мишень с вероятностью 0,8, а второй