Случайный вектор (𝜉, 𝜂) распределен равномерно в области 𝐺, изображенной на рисунке.

		Математическая статистика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16444
		Прошла проверку преподавателем МГУ
		245 руб.

Случайный вектор (𝜉, 𝜂) распределен равномерно в области 𝐺, изображенной на рисунке.

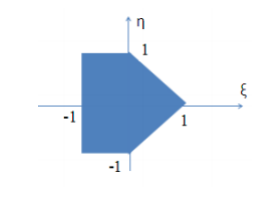
1) Найти плотность распределения вероятностей компонент случайного вектора и решить вопрос об их зависимости или независимости. 2) Выяснить, коррелированы ли компоненты случайного вектора (𝜉, 𝜂). 3) Найти 𝑃{(𝜉, 𝜂) ∈ 𝐷}, где 𝐷 = {(𝑥, 𝑦)|𝑥 2 + 𝑦 2 ≤ 1}.

Решение

1) Поскольку случайный вектор (𝜉, 𝜂) распределен равномерно в области 𝐺, то плотность распределения системы случайного вектора (𝜉, 𝜂) имеет вид:  Определим константу 𝐴, используя условие нормировки Определим уравнения, ограничивающие область 𝐺. Разбивая область интегрирования на две прямой 𝑥 = 0, получим Тогда 3𝐴 = 1 𝐴 = 1 3 Плотность распределения системы случайного вектора (𝜉, 𝜂) имеет вид:  Найдем плотность распределения вероятностей компонент случайного вектора (𝜉, 𝜂). Очевидно, что при 𝑥 > 1 и при 𝑥 < −1 плотность распределения . Аналогично при 𝑦 > 1 и при 𝑦 < −1 плотность распределения 𝑓(𝑦) = 0. Пусть Тогда