Автор Анна Евкова
Преподаватель который помогает студентам и школьникам в учёбе.

Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения

Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения Математический анализ
Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения Решение задачи
Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения
Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения Выполнен, номер заказа №16309
Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения Прошла проверку преподавателем МГУ
Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения  245 руб. 

Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения

Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!

Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения

Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):

Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 

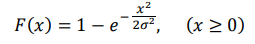
Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения

Найти: а) моду распределения; б) медиану распределения; в) плотность вероятности 𝑓(𝑥).

Решение

а) Модой непрерывного распределения является такое значение 𝑋, которое соответствует максимуму функции плотности распределения. Плотность распределения вероятности 𝑓(𝑥) найдем по формуле: Экстремумы функции 𝑓(𝑥) ищем в нулях первой производной Определим знак 𝑓′(𝑥) на каждом интервале: Из таблицы видно, что функция возрастает при и убывает при . Поскольку функция плотности вероятности максимальна при мода б) Медиана – решение уравнения Тогда в) Плотность распределения вероятности 𝑓(𝑥) определена выше Ответ: 𝑀0 = 𝜎; 𝑀𝑒 = √2𝑙𝑛2 = 𝜎; 𝑓(𝑥) = 𝑒 − 𝑥 2 2𝜎2 ∙ 𝑥 𝜎2

Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея: 𝐹(𝑥) = 1 − 𝑒 − 𝑥 2 2𝜎2 , (𝑥 ≥ 0) Найти: а) моду распределения