Случайная величина 𝑋 в интервале (0; 𝜋 2 ) задана плотностью распределения 𝑓(𝑥) = 𝑐𝑜𝑠𝑥; вне этого интервала 𝑓(𝑥) = 0. Найти дисперсию функции 𝑌 = 𝜑(𝑋) = 𝑋 2 находя предварительно

		Математический анализ
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16309
		Прошла проверку преподавателем МГУ
		245 руб.

Случайная величина 𝑋 в интервале 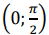задана плотностью распределения 𝑓(𝑥) = 𝑐𝑜𝑠𝑥; вне этого интервала 𝑓(𝑥) = 0. Найти дисперсию функции 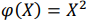находя предварительно плотности распределения 𝑌.

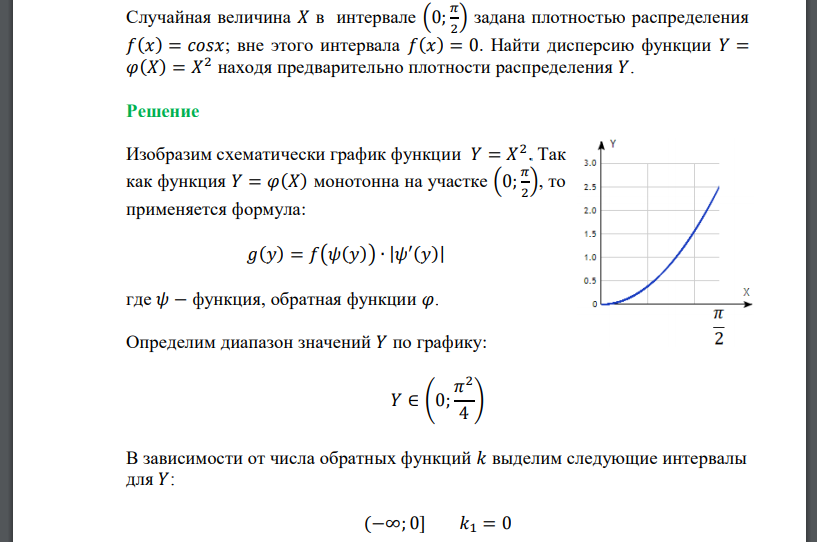
Решение

Изобразим схематически график функции Так как функция монотонна на участке то применяется формула: где 𝜓 − функция, обратная функции 𝜑. Определим диапазон значений 𝑌 по графику: В зависимости от числа обратных функций 𝑘 выделим следующие интервалы для 𝑌: В интервалах обратные функции не существуют, следовательно, плотность вероятности Решение задачи оформим в виде двух столбцов: в левом будут помещены обозначения функции, принятые в общем решении задачи, в правом – конкретные функции, соответствующие данному примеру: Таким образом, плотность распределения вероятности величины 𝑌 равна: Математическое ожидание случайной величины 𝑌 равно: Воспользуемся заменой тогда Найдем отдельно неопределенный интеграл вида используя формулу интегрирования по частям Тогда: Воспользуемся заменой тогда При получим При получим Найдем отдельно неопределенный интеграл вида используя формулу интегрирования по частям Дисперсия равна: Ответ: 𝐷(𝑌) = 0,2608