Автор Анна Евкова
Преподаватель который помогает студентам и школьникам в учёбе.
Случайная величина 𝑋 в интервале (−1; 1) задана плотностью распределения 𝑓(𝑥) = 1 𝜋√1−𝑥 2 ; вне этого интервала 𝑓(𝑥) = 0. Найти: а) моду; б) медиану 𝑋.
 |
 |
Математический анализ |
 |
 |
Решение задачи |
 |
 |
|
 |
 |
Выполнен, номер заказа №16290 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
|
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл! |
|
Закажите у меня новую работу, просто написав мне в чат! |
Описание заказа и 38% решения ( + фото):
Случайная величина 𝑋 в интервале (−1; 1) задана плотностью распределения 𝑓(𝑥) = 1 𝜋√1−𝑥 2 ; вне этого интервала 𝑓(𝑥) = 0. Найти: а) моду; б) медиану 𝑋.
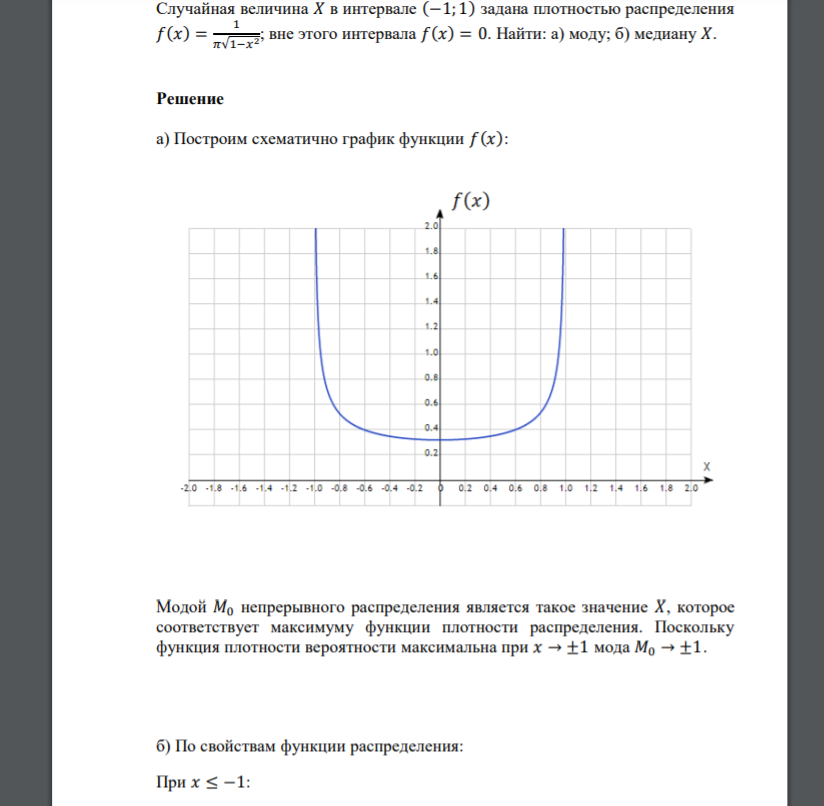
Решение
а) Построим схематично график функции 𝑓(𝑥): Модой 𝑀0 непрерывного распределения является такое значение 𝑋, которое соответствует максимуму функции плотности распределения. Поскольку функция плотности вероятности максимальна при
б) По свойствам функции распределения: Тогда функция распределения 𝐹(𝑥) имеет вид: Медиана 𝑀𝑒 непрерывного распределения – это решение уравнения: Тогда
Похожие готовые решения по математическому анализу:
- Случайная величина 𝑋 распределена по закону 𝑓(𝑥). Найти: 1) величину 𝐶; 2) функцию распределения 𝐹(𝑥); 3) построить графики функций 𝑓(𝑥) и 𝐹(𝑥). 𝑓(𝑥) = { 0
- Задана функция 𝑓(𝑥) = { 𝐴√𝑥, 𝑥 ∈ [0,4] 0, 𝑥 ∉ [0,4] Определить значение параметра 𝐴, при котором эта функция задает плотность распределения некоторой непрерывной СВ 𝑋.
- Случайная величина 𝑋 в интервале (−𝑐; 𝑐) задана плотностью распределения: 𝑓(𝑋) = 1 𝜋√𝑐 2−𝑥 2 , вне этого интервала 𝑓(𝑋) = 0. Найти математическое ожидание случайной величины 𝑋.
- Найти параметр 𝐴, математическое ожидание и дисперсию случайной величины 𝜉, плотность вероятностей которой: 𝑓(𝑥) = { 𝐴 √3 2 − 𝑥 2 , при 𝑥 ∈ (−3; 3) 0, при |𝑥| ≥ 3 Найти 𝑃 {0 < 𝜉 < 3 2 }. Построить график
- Случайная величина 𝑋 задана дифференциальной функцией распределения 𝑓(𝑥) = { 0, 𝑥 ≤ −1 𝐴 ∙ 1 √1 − 𝑥 2 , − 1 < 𝑥 ≤ 1 0, 𝑥 > 1 a) Найти параметр 𝐴; b) Найти интегральную функцию 𝐹(𝑥), математическое ожидание
- Задана плотность распределения случайной величины 𝑓(𝑥). Найти: значение параметра 𝑐, функцию распределения 𝐹(𝑥), математическое ожидание. Построить
- Случайная величина 𝑋 задана функцией плотности распределения: 𝑓(𝑥) = { 0, 𝑥 ∉ [1; 32] 𝐶𝑥 3 5, 𝑥 ∈ [1; 32] а) Найдите значение константы 𝐶. б) Постройте график
- Определить при каком значении параметра 𝐶 заданная функция 𝑓(𝑥) является функцией плотности распределения случайной величины. Найти функцию
- Вероятность появления события 𝐴 равна 0,3. Найти вероятность того, что в 7 испытаниях событие 𝐴 появится
- Найти вероятность того, что в 7 независимых испытаниях событие появится: a) ровно 4 раза, b) хотя бы
- Случайная величина 𝑋 распределена по закону 𝑓(𝑥). Найти: 1) величину 𝐶; 2) функцию распределения 𝐹(𝑥); 3) построить графики функций 𝑓(𝑥) и 𝐹(𝑥). 𝑓(𝑥) = { 0
- В опыте событие 𝐴 происходит с вероятностью 1/3 . Опыт производится 7 раз. Найти вероятность