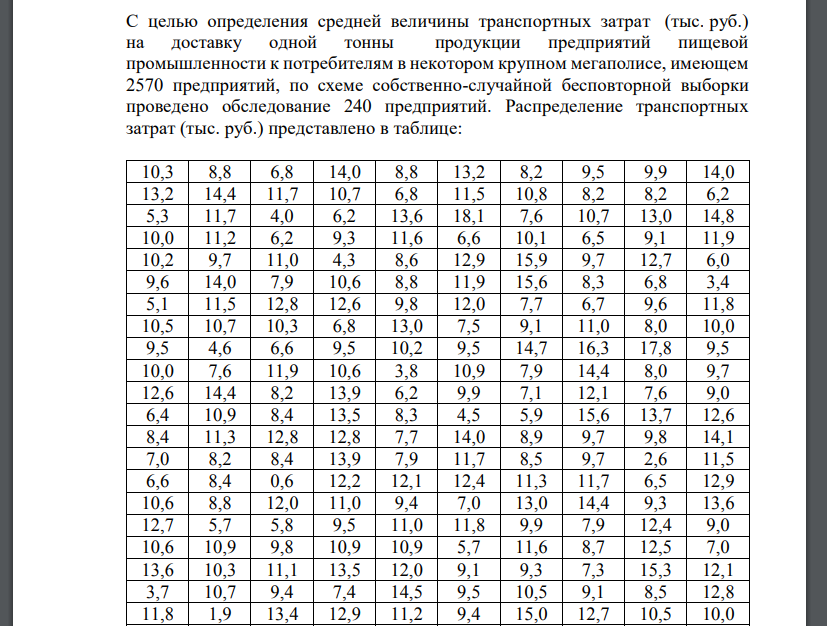
С целью определения средней величины транспортных затрат (тыс. руб.) на доставку одной тонны продукции предприятий пищевой промышленности

		Математическая статистика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16423
		Прошла проверку преподавателем МГУ
		245 руб.

С целью определения средней величины транспортных затрат (тыс. руб.) на доставку одной тонны продукции предприятий пищевой промышленности к потребителям в некотором крупном мегаполисе, имеющем 2570 предприятий, по схеме собственно-случайной бесповторной выборки проведено обследование 240 предприятий. Распределение транспортных затрат (тыс. руб.) представлено в таблице:

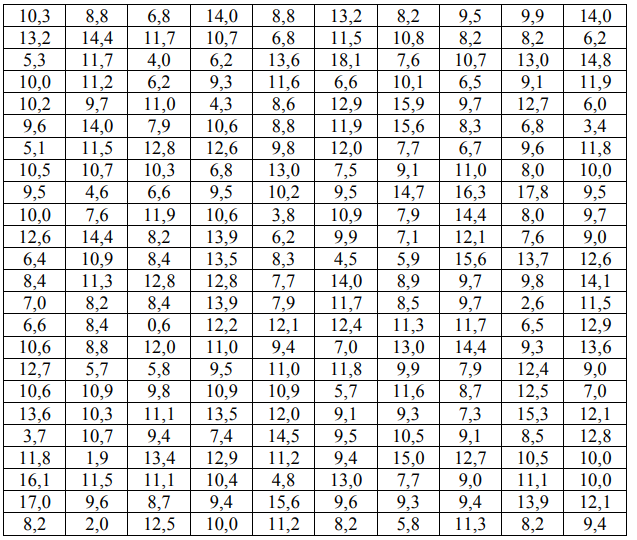
Составить интервальный вариационный ряд. Записать эмпирическую функцию распределения и построить ее график. На одном чертеже изобразить гистограмму и полигон частот. По сгруппированным данным вычислить выборочные числовые характеристики: среднее арифметическое, исправленную выборочную дисперсию, среднее квадратичное отклонение, коэффициент вариации, асимметрию, эксцесс, моду и медиану. Заменив параметры генеральной совокупности соответственно их наилучшими выборочными числовыми характеристиками и используя 𝜉 2 - критерий Пирсона, на уровне значимости  = 0,05 проверить две гипотезы о том, что изучаемая случайная величина 𝜉 – величина транспортных затрат – распределена: а) по нормальному закону распределения; б) по равномерному закону распределения. Построить на чертеже, на котором изображена гистограмма эмпирического распределения, соответствующие графики равномерного и нормального распределений.

Решение

Построим вариационный ряд – выборку в порядке возрастания:  Определим минимальное и максимальное значение. Размах выборки 𝑅𝑥 равен: 𝑅 Число интервалов 𝑁 связано с объемом выборки соотношением:Длина частичного интервала ℎ равна: За нижнюю границу первого интервала возьмём 0,3. Найдем число значений, попавших в каждый интервал. Относительные частоты (частости) 𝑚∗ определим по формуле: