С целью определения средней суммы вкладов на 1 января текущего года в сберегательном банке, имеющем 2000 вкладчиков, по схеме

		Математическая статистика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16423
		Прошла проверку преподавателем МГУ
		245 руб.

С целью определения средней суммы вкладов на 1 января текущего года в сберегательном банке, имеющем 2000 вкладчиков, по схеме собственнослучайной выборки с бесповторным отбором членов проведено обследование 200 лицевых счетов. Распределение вкладов по их величине (тыс. руб.) представлено в таблице. Заменив неизвестные параметры генеральной совокупности соответственно их наилучшими выборочными оценками, по данным задачи 4, используя 𝜒 2 - критерий Пирсона, на уровне значимости =0,05 проверить две гипотезы о том, что изучаемая случайная величина ξ – величина вклада – распределена: а) по нормальному закону распределения; б) по равномерному закону распределения. Построить на чертеже, где изображена гистограмма эмпирического распределения, соответствующие графики равномерного и нормального распределений.

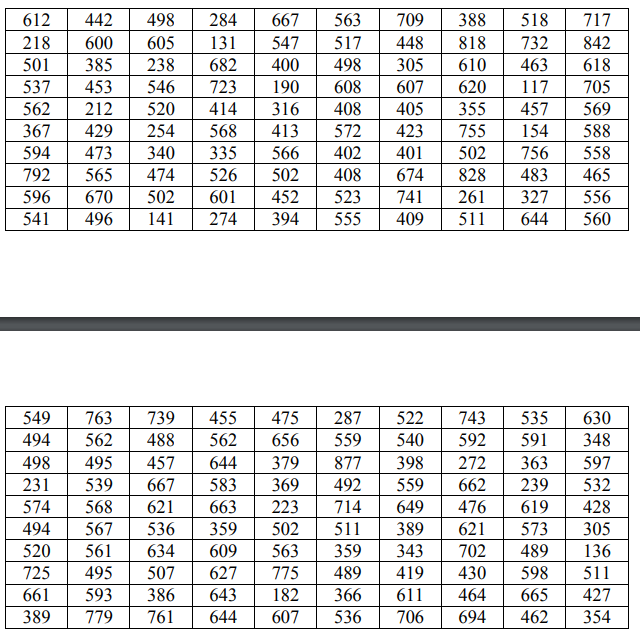
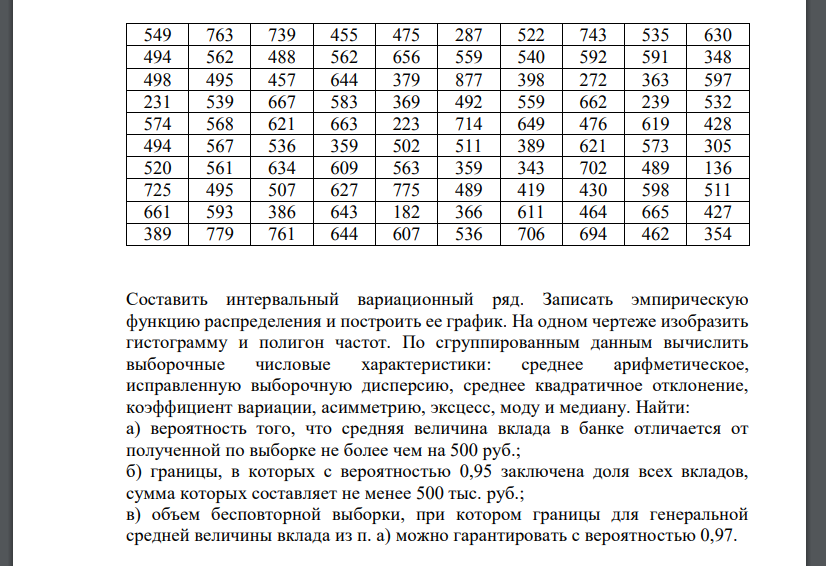
Составить интервальный вариационный ряд. Записать эмпирическую функцию распределения и построить ее график. На одном чертеже изобразить гистограмму и полигон частот. По сгруппированным данным вычислить выборочные числовые характеристики: среднее арифметическое, исправленную выборочную дисперсию, среднее квадратичное отклонение, коэффициент вариации, асимметрию, эксцесс, моду и медиану. Найти: а) вероятность того, что средняя величина вклада в банке отличается от полученной по выборке не более чем на 500 руб.; б) границы, в которых с вероятностью 0,95 заключена доля всех вкладов, сумма которых составляет не менее 500 тыс. руб.; в) объем бесповторной выборки, при котором границы для генеральной средней величины вклада из п. а) можно гарантировать с вероятностью 0,97.

Решение

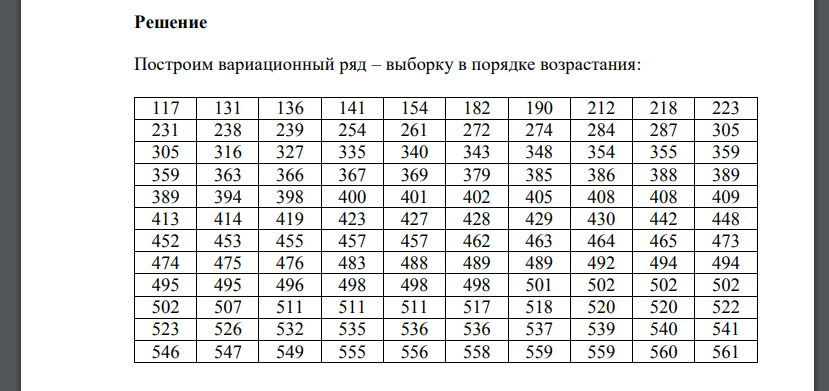
Построим вариационный ряд – выборку в порядке возрастания:   Найдем размах выборки  Число интервалов 𝑁, на которые следует разбить интервал значений признака, найдём по формуле Стерджесса: где n − объём выборки, то есть число единиц наблюдения. В данном случае  Получим:  Рассчитаем шаг (длину частичного интервала) ℎ по формуле: Подсчитаем частоту каждого интервала, то есть число вариант, попавших в этот интервал. Варианты, совпадающие с границами частичных интервалов, включают в правый интервал. Относительные частоты 𝑚∗ определим по формуле:Запишем в виде таблицы интервальный вариационный ряд.