С целью изучения дневной выборки ткани (м) ткачихами комбината по схеме собственно-случайной выборки было отобрано 100 ткачих

		Математическая статистика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16472
		Прошла проверку преподавателем МГУ
		245 руб.

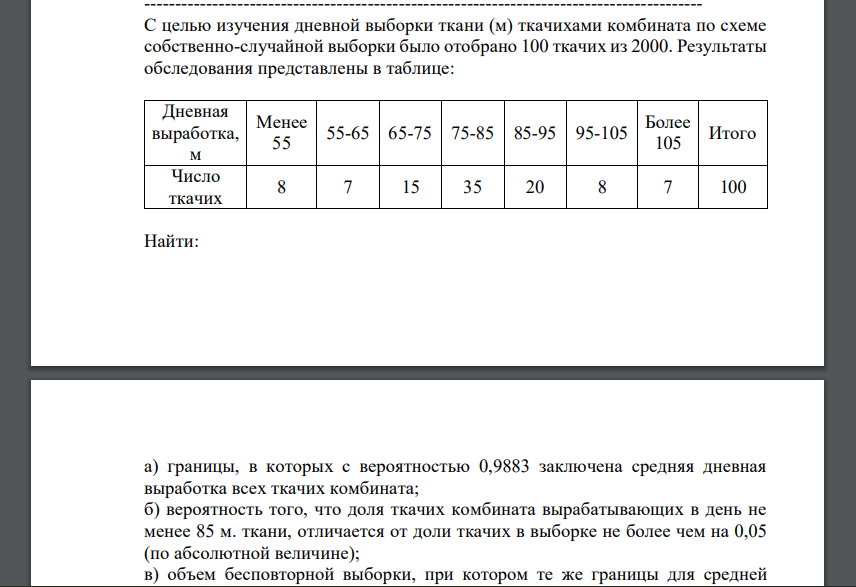
С целью изучения дневной выборки ткани (м) ткачихами комбината по схеме собственно-случайной выборки было отобрано 100 ткачих из 2000. Результаты обследования представлены в таблице: Дневная выработка, м Менее 55 55-65 65-75 75-85 85-95 95-105 Более 105 Итого Число ткачих 8 7 15 35 20 8 7 100 Найти: а) границы, в которых с вероятностью 0,9883 заключена средняя дневная выработка всех ткачих комбината; б) вероятность того, что доля ткачих комбината вырабатывающих в день не менее 85 м. ткани, отличается от доли ткачих в выборке не более чем на 0,05 (по абсолютной величине); в) объем бесповторной выборки, при котором те же границы для средней дневной выработки (см. п. а)) можно гарантировать с вероятностью 0,9942.

Решение

Найдем выборочное среднее  Выборочная дисперсия: 𝑆 Исправленное среднеквадратичное отклонение   а) Средняя квадратическая ошибка при оценке генеральной средней для собственно-случайной бесповторной выборки достаточно большого объема, находится по формуле:  Предельная ошибка бесповторной выборки равна: ∆= 𝑡 ∙ 𝜎𝑥̅ ′ где 𝑡 – такое значение аргумента функции Лапласа, при котором Ф(𝑡) = 1 2 𝛾. По таблице функции Лапласа находим 𝑡 из равенства: