Провести статистическую обработку массива данных в столбцах N,M,K из общей таблицы 5 6 8 567 559 555 563 574 562 560 565 558 570 582 565 559 558

		Теория вероятностей
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16412
		Прошла проверку преподавателем МГУ
		245 руб.

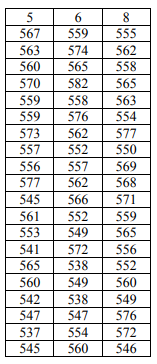
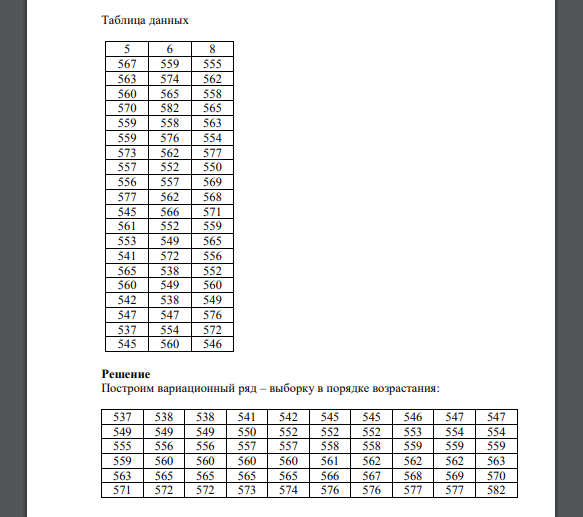
Провести статистическую обработку массива данных в столбцах N,M,K из общей таблицы, представленной ниже. Ранжировать данные по величине и найти размах выборки. Преобразовать точечный вариационный ряд в интервальный с числом интервалов 8. Построить полигон и гистограмму. Найти выборочные моду и медиану. Найти выборочное среднее, дисперсию и СКО. Проверить гипотезу о нормальном распределении генеральной совокупности с помощью критерия Пирсон на уровне значимости 𝛼. Найти доверительный интервал для математического ожидания генеральной совокупности с надежностью 𝛾. Вариант Номера столбцов 𝛼 𝛾 4 5,6,8 0.2 0.9 Таблица данных 5 6 8 567 559 555 563 574 562 560 565 558 570 582 565 559 558 563 559 576 554 573 562 577 557 552 550 556 557 569 577 562 568 545 566 571 561 552 559 553 549 565 541 572 556 565 538 552 560 549 560 542 538 549 547 547 576 537 554 572 545 560 546

Решение

Построим вариационный ряд – выборку в порядке возрастания:  Найдем размах выборки  Рассчитаем шаг (длину частичного интервала) ℎ по формуле (где 8 – заданное в условии число интервалов): Округление шага производится, как правило, в большую сторону. Таким образом, принимаем. За начало первого интервала принимаем такое значение из интервала чтобы середина полученного интервала оказалась удобным для расчетов числом. В данном случае за нижнюю границу первого интервала возьмём 535. Подсчитаем частоту 𝑛𝑖 каждого интервала, то есть число вариант, попавших в этот интервал. Варианты, совпадающие с границами частичных интервалов, включают в левый интервал. Относительные частоты (частости) 𝑓𝑖 определим по формуле:  Плотность относительной частоты определим по формуле:  Построим интервальный вариационный ряд частот с равными интервалами. Номер интервала Интервал Середина интервала 𝑥𝑖 Частота  Построим полигон частот. Построим гистограмму. Для интервального ряда (с равными интервалами) мода определяется по следующей формуле:  нижнее значение модального интервала; частота в модальном интервале; частота в предыдущем интервале;  частота в следующем интервале за модальным; ℎ – размах интервала. Модальный интервал – это интервал с наибольшей частотой, т.е. в данном случае. Тогда  Медианой в статистике называют варианту, расположенную в середине вариационного ряда. Для интервального ряда медиану определяют по формуле: нижняя граница интервала, в котором находится медиана; ℎ – размах интервала;  накопленная частота в интервале, предшествующем медианному;  частота в медианном интервале. Медианный интервал – это тот, на который приходится середина ранжированного ряда, т.е. в данном случае  Выборочное среднее значение 𝑥̅в равно:  Выборочная дисперсия равна:  Выборочное среднее квадратическое отклонение  Несмещенная (исправленная) оценка генеральной дисперсии:  Исправленное среднеквадратичное отклонение  Проверим гипотезу о нормальном распределении генеральной совокупности по критерию Пирсона (на уровне значимости 𝛼 = 0,2). Вероятность попадания случайной величины в каждый интервал равна:  Теоретические частоты определим по формуле 𝑛𝑖 ′ = 𝑛 ∙ 𝑝𝑖 и вычислим значения Результаты запишем в таблицу Интервал  Здесь объединены первые два и последние два интервала, чтобы выполнялось условие. В итоге получили интервалов, число степеней свободы для  распределения равно. Получили По таблице при уровне значимости  находим. Так как, то нет оснований отвергать гипотезу о нормальном распределении при заданном уровне значимости. Доверительный интервал для математического ожидания a равен: такое значение аргумента функции Лапласа, при котором . По таблице функции Лапласа находим 𝑡 из равенства:  Получаеми искомый доверительный интервал имеет вид: