По заданному варианту выборочной совокупности независимых измерений случайной величины Х (СВ Х) (предварительно удалив резко выделяющиеся наблюдения

		Экономика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №17342
		Прошла проверку преподавателем МГУ
		245 руб.

II. Задание по теме «Статистический анализ одномерных случайных величин»

По заданному варианту выборочной совокупности независимых измерений случайной величины Х (СВ Х) (предварительно удалив резко выделяющиеся наблюдения):

1. Составить интервальный статистический ряд распределения относительных частот, построить гистограмму и полигон относительных частот.

2. Найти эмпирическую функцию распределения и построить ее график.

3. Вычислить точечные оценки для математического ожидания, дисперсии, коэффициентов асимметрии и эксцесса.

4. Исходя из общих представлений о механизме образования СВ Х, а также по виду гистограммы и полигона относительных частот и вычисленным числовым характеристикам, выдвинуть гипотезу и виде закона распределения СВ Х; записать плотность распределения вероятностей и функцию распределения для выдвинутого гипотетического закона, заменяя параметры закона вычисленными для них оценками.

5. Вычислить интервальные оценки для математического ожидания и среднеквадратического отклонения, соответствующие доверительным вероятностям р=0.95 и р=0.99.

Исходные данные:

Данные о промежутках времени между поступлениями заказов на такси в минутах (округлены с избытком с точностью до 1 мин)

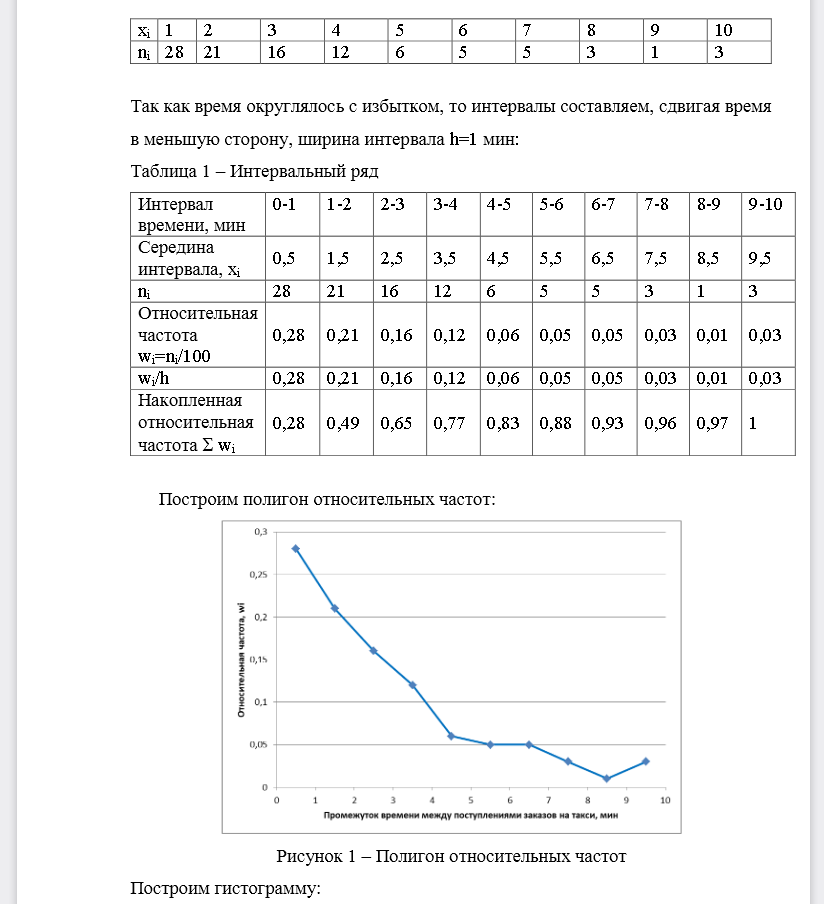
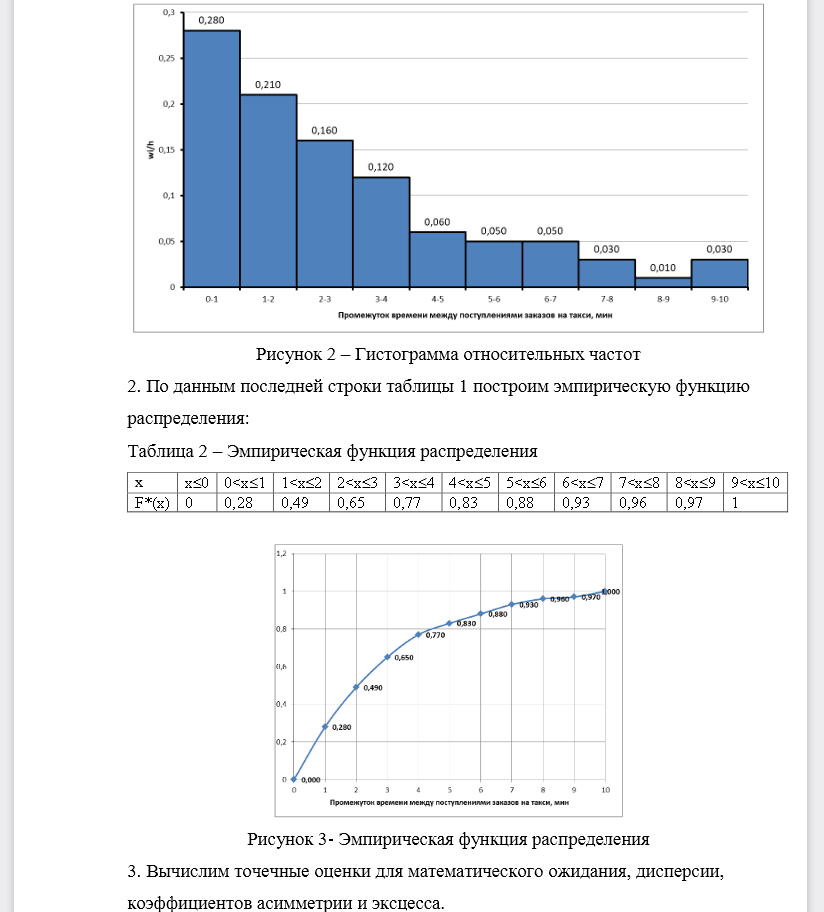
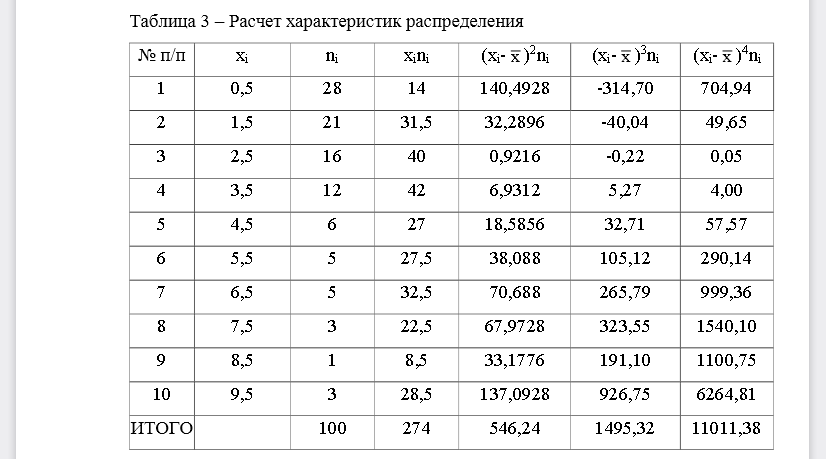
РЕШЕНИЕ 1. Составим дискретный ряд: Так как время округлялось с избытком, то интервалы составляем, сдвигая время в меньшую сторону, ширина интервала h=1 мин: Таблица 1 – Интервальный ряд Построим полигон относительных частот: Рисунок 1 –Полигон относительных частот Построим гистограмму: Рисунок 2 –Гистограмма относительных частот 2. По данным последней строки таблицы 1 построим эмпирическую функцию распределения: Таблица 2 –Эмпирическая функция распределения Рисунок 2 –Гистограмма относительных частот 2. По данным последней строки таблицы 1 построим эмпирическую функцию распределения: Таблица 2 –Эмпирическая функция распределения Рисунок 3-Эмпирическая функция распределения 3. Вычислим точечные оценки для математического ожидания, дисперсии, коэффициентов асимметрии и эксцесса. Таблица 3 –Расчет характеристик распределения Выборочная средняя: Дисперсия: Исправленная дисперсия: Среднее квадратическое отклонение:  мин Исправленное среднее квадратическое отклонение:  мин Коэффициент асимметрии: Коэффициент эксцесса: Таким образом, распределение имеет правостороннююасимметрию и является островершинным (по сравнению с нормальным. 4. Исходя из общих представлений о механизме образования СВ Х, а также по виду гистограммы и полигона относительных частот и вычисленным числовым характеристикам, можно выдвинуть гипотезу отом, что время между поступлениями заказов на такси распределено по показательному закону, следовательно примем, что неизвестная плотность теоретического распределения имеет вид: Наилучшим значением параметра является  В качестве теоретической кривой возьмем график функции: Найдем теоретические значения и т.д. Построим на одном графике эмпирическую плотность распределения Рисунок 4 –Теоретическая и эмпирическая плотность распределения Как видно, графики близки друг к другу, поэтому можно для данной СВ Х принять показательный закон распределения5. Вычислить интервальные оценки для математического ожидания и среднеквадратического отклонения, соответствующие доверительным вероятностям р=0.95 и р=0.99. Доверительный интервал для оценки математического ожидания (среднего значения) находится по формуле: где n=100–объем выборки s=2,349 – исправленное среднее квадратическое отклонение Для 95%:  –значение, находим по таблице распределения Стьюдента Построим доверительный интервал для СКО По таблице значений находим  Так как q<1, то для оценки применяется формула: Для 99%: Построим доверительный интервал для СКО По таблице значений находим  Так как q<1, то для оценки применяется формула: