
По выборке объема 𝑛 = 100, извлеченной из двумерной нормальной генеральной совокупности (𝑋; 𝑌) составлена корреляционная
 |
 |
Математическая статистика |
 |
 |
Решение задачи |
 |
 |
|
 |
 |
Выполнен, номер заказа №16472 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
|
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл! |
|
Закажите у меня новую работу, просто написав мне в чат! |
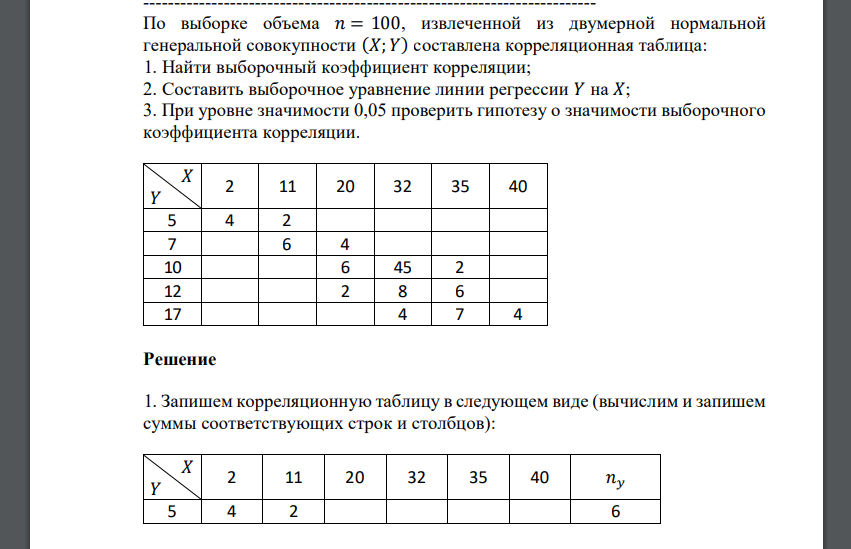
По выборке объема 𝑛 = 100, извлеченной из двумерной нормальной генеральной совокупности (𝑋; 𝑌) составлена корреляционная таблица: 1. Найти выборочный коэффициент корреляции; 2. Составить выборочное уравнение линии регрессии 𝑌 на 𝑋; 3. При уровне значимости 0,05 проверить гипотезу о значимости выборочного коэффициента корреляции. 𝑋 𝑌 2 11 20 32 35 40 5 4 2 7 6 4 10 6 45 2 12 2 8 6 17 4 7 4
Решение
1. Запишем корреляционную таблицу в следующем виде (вычислим и запишем суммы соответствующих строк и столбцов): 𝑋 Найдем необходимые числовые характеристики. Выборочные средние: Откуда получаем: и ковариация: Определим коэффициент корреляции . Составим выборочное уравнение линии регрессии 𝑌 на 𝑋:

- На колонке длиной 3 м расстояние удерживания одного из компонентов равно 20 мм, а полуширина хроматографического
- Найти выборочное уравнение прямой регрессии 𝑌 на 𝑋 по данной корреляционной таблице. 𝑌 𝑋 11 16
- Рассчитайте объем 0,01 М раствора натрия тиосульфата (КП = 0,9800), который будет израсходован на титрование избытка 0,01 М раствора йода при определении содержания нитрофурала
- Построить кривые потенциометрического титрования в координатах E-V и ΔE/ΔV-V. Определить концентрацию НСl, если при титрованииПостроить кривые потенциометрического титрования в координатах E-V и ΔE/ΔV

