Автор Анна Евкова
Преподаватель который помогает студентам и школьникам в учёбе.

По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2

По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2 По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2 Теория вероятностей
По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2 По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2 Решение задачи
По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2 По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2
По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2 По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2 Выполнен, номер заказа №16412
По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2 По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2 Прошла проверку преподавателем МГУ
По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2 По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2  245 руб. 

По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2

Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!

По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2

Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):

По имеющимся данным требуется:

1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона или гистограммы. Найти функцию распределения, построить ее график. 

2. Найти: выборочную среднюю, выборочную дисперсию, среднее квадратическое отклонение выборки, моду и медиану.

3. Проверить при уровне значимости α=0.05 гипотезу о соответствии имеющего статистического распределения нормальному закону.

4. Считая данные нормально распределенной случайной величиной найти: 

а) точечную оценку математического ожидания изучаемой совокупности;

б) доверительный интеграл для математического ожидания с доверительной вероятностью 0,95.

По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2

Решение

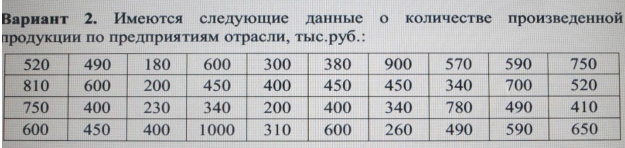
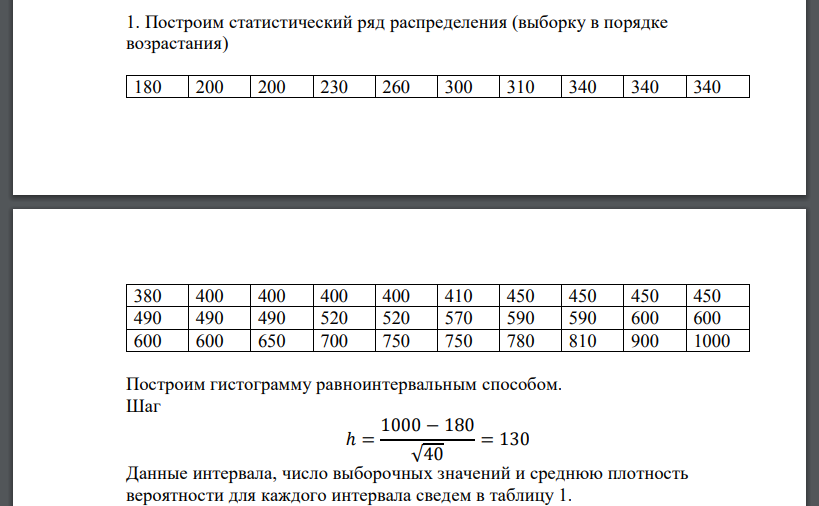
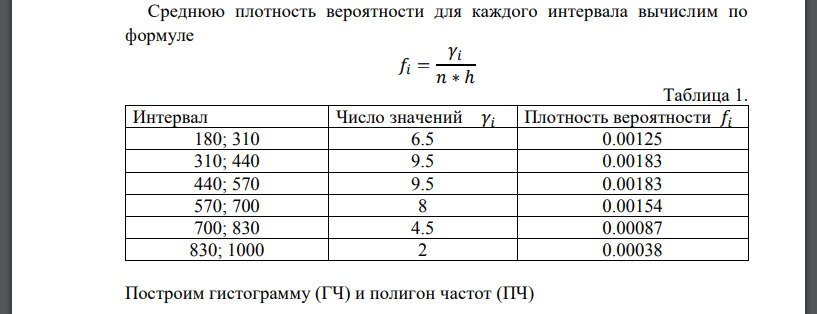
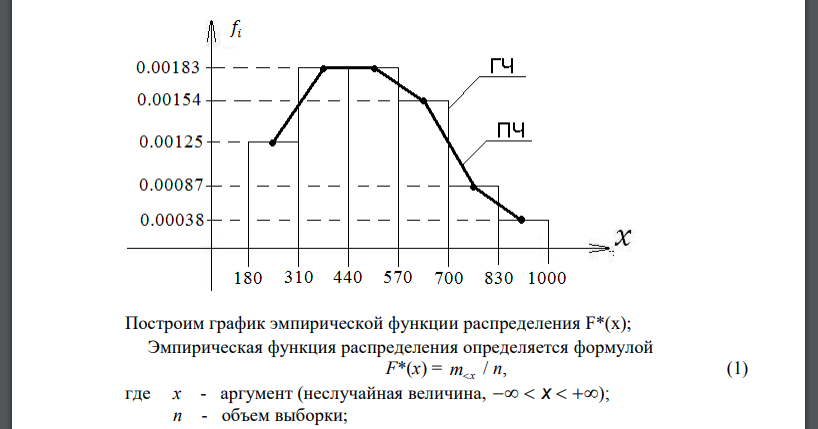
1. Построим статистический ряд распределения (выборку в порядке возрастания) Построим гистограмму равноинтервальным способом. Шаг Данные интервала, число выборочных значений и среднюю плотность вероятности для каждого интервала сведем в таблицу 1. Среднюю плотность вероятности для каждого интервала вычислим по формуле Построим гистограмму (ГЧ) и полигон частот (ПЧ) Построим график эмпирической функции распределения F*(x); Эмпирическая функция распределения определяется формулой где x - аргумент (неслучайная величина); n - объем выборки; количество значений в выборке или вариационном ряду, строго меньших x. На числовой оси x выделим полуинтервалы (Ai , Bi ], на которых функция F*(x) не изменяет своего значения. Границы полуинтервалов определяем соседними отличающимися значениями вариационного ряда. На каждом полуинтервале по формуле (1) вычисляем значение функции F*(x). 2) Выборочное среднее 𝑥̅ равно Выборочная дисперсия равна: Исправленное среднее квадратическое отклонение S равно: Модой случайной величины называется ее наиболее вероятное значение, т.е. то значение, для которого f(x) (для непрерывных СВ) достигает максимума. либо Медианой случайной величины X называется такое ее значение, для которого выполняется условие 

По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2

По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2

По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2

По имеющимся данным требуется: 1. Построить статистический ряд распределения, изобразить получившийся ряд, графически с помощью полигона Вариант 2