Автор Анна Евкова
Преподаватель который помогает студентам и школьникам в учёбе.

Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Тре

Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Тре Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Тре Математический анализ
Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Тре Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Тре Решение задачи
Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Тре Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Тре
Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Тре Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Тре Выполнен, номер заказа №16310
Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Тре Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Тре Прошла проверку преподавателем МГУ
Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Тре Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Тре  245 руб. 

Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Тре

Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!

Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Тре

Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):

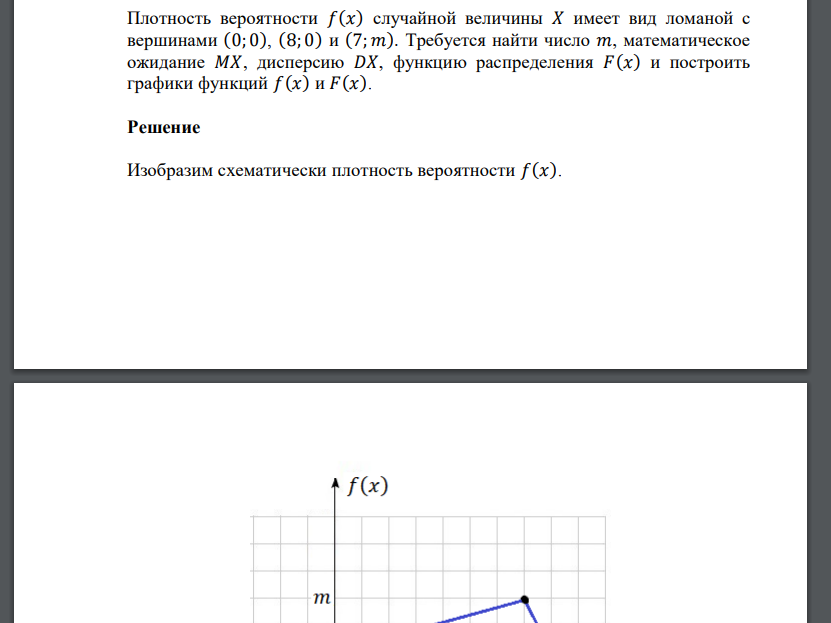
Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Требуется найти число 𝑚, математическое ожидание 𝑀𝑋, дисперсию 𝐷𝑋, функцию распределения 𝐹(𝑥) и построить графики функций 𝑓(𝑥) и 𝐹(𝑥).

Решение

Изобразим схематически плотность вероятности 𝑓(𝑥). По свойству функции плотности распределения: Интеграл представляет собой площадь прямоугольного треугольника, которая равна: откуда: Уравнение прямой, проходящей через две заданные точки имеет вид Для точек ( Для точек (8; 0) и  Функция плотности распределения вероятности принимает вид: Математическое ожидание: Дисперсия 𝐷𝑋 равна: Найдем функцию распределения 𝐹(𝑥). По свойствам функции распределения: При  При Тогда функция распределения имеет вид: Построить графики функций 𝑓(𝑥) и 𝐹(𝑥)

Плотность вероятности 𝑓(𝑥) случайной величины 𝑋 имеет вид ломаной с вершинами (0; 0), (8; 0) и (7; 𝑚). Тре

Похожие готовые решения по математическому анализу: