Автор Анна Евкова
Преподаватель который помогает студентам и школьникам в учёбе.

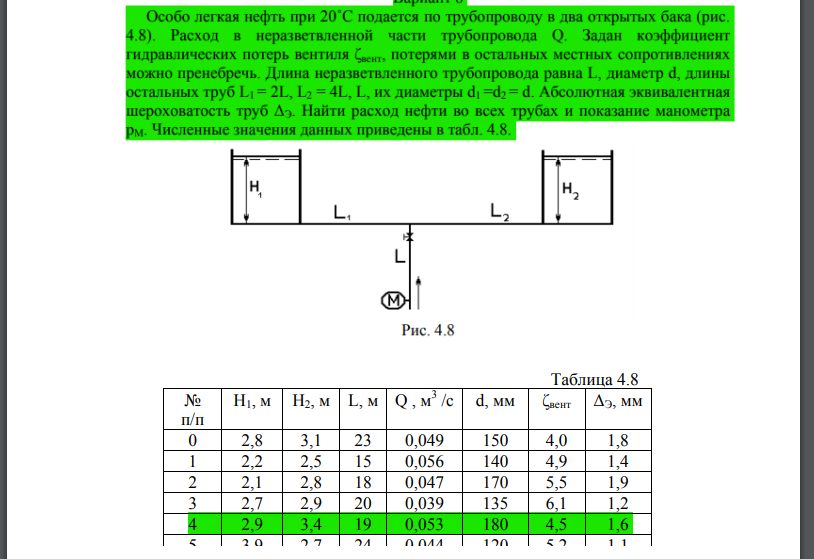
Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент

Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент Физика
Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент Решение задачи
Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент
Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент Выполнен, номер заказа №16683
Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент Прошла проверку преподавателем МГУ
Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент  245 руб. 

Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент

Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!

Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент

Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):

Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент гидравлических потерь вентиля, потерями в остальных местных сопротивлениях можно пренебречь. Длина неразветвленного трубопровода равна L, диаметр d, длины остальных труб..., их диаметры. Абсолютная эквивалентная шероховатость труб. Найти расход нефти во всех трубах и показание манометра. Численные значения данных приведены в табл. 4,8.

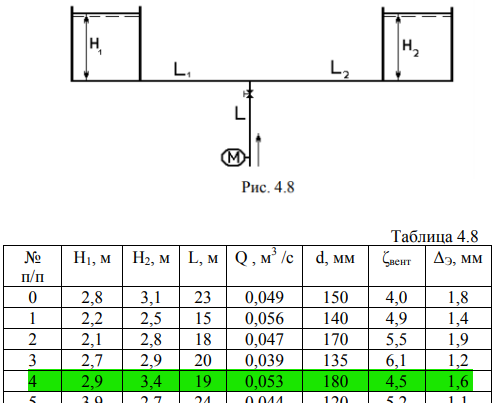
Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент

Решение

Считаем трубопроводы длинными, местными потерями (кроме потерь в вентиле) пренебрегаем. Кроме того, принимаем, что на неразветвлённом участке расходы суммируются.  Решим задачу, записывая уравнения Бернулли для всех ветвей по отдельности. Для неразветвленной части, обозначив Н напор в узле, запишем: данном случае  предположим, что имеет место квадратичный режим течения, и для определения коэффициента потерь на трение по длине можно использовать формулу Шифринсона: Очевидно, что для параллельных ветвей движение жидкости происходит под разностью напоров в соответствующем баке и точке разветвления.

Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент

Особо легкая нефть при 200С подается по трубопроводу в два закрытых бака (рис. 4,8). Расход в неразветвленной части трубопровода Q. Задан коэфициент