
Однородный цилиндр массой т1 = 3 кг может вращаться вокруг вертикальной оси, совпадающей с его осью симметрии.
 |
 |
Физика |
 |
 |
Решение задачи |
 |
 |
|
 |
 |
Выполнен, номер заказа №16520 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
|
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл! |
|
Закажите у меня новую работу, просто написав мне в чат! |
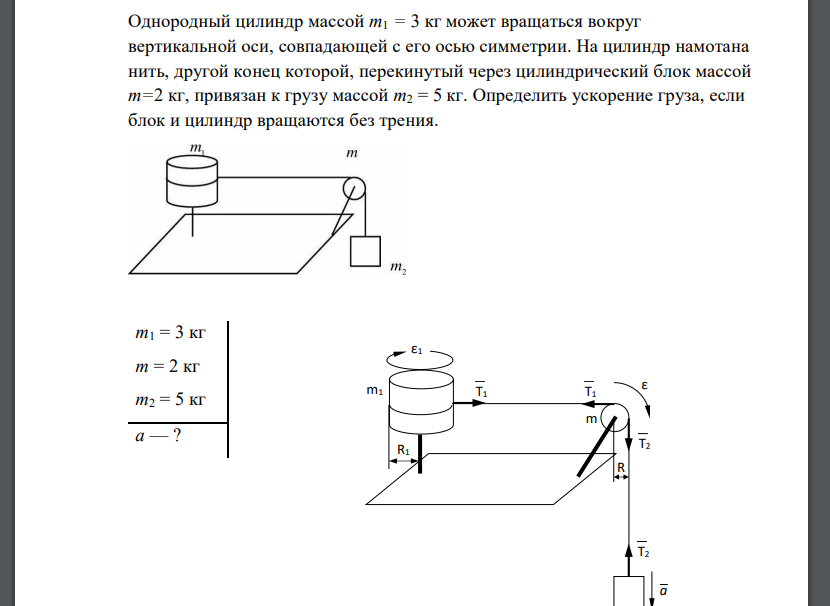
Однородный цилиндр массой т1 = 3 кг может вращаться вокруг вертикальной оси, совпадающей с его осью симметрии. На цилиндр намотана нить, другой конец которой, перекинутый через цилиндрический блок массой т=2 кг, привязан к грузу массой т2 = 5 кг. Определить ускорение груза, если блок и цилиндр вращаются без трения.
Момент инерции цилиндра .Момент инерции блока .mR На основании второго закона Ньютона для груза запишем a Основное уравнение динамики вращающихся телгде Т1 и Т2 — силы натяжения нити; R1 — радиус цилиндра; R — радиус блока. Уравнения связи между ускорениями: , ,где — угловые ускорения цилиндра и блока соответсвенно, a — ускорение груза. Из системы уравнений (2)—(3) получим: Суммируя почленно уравнения системы, исключаем . Подставив выражение для T2 в уравнение (1), находим ускорение груза: Ответ:

- Вероятность появления опечатки на странице книги, содержащей 100 страниц, равна 0,03. Найти вероятность того
- Какую нужно совершить работу А, чтобы пружину жесткостью k = 800 Н/м, сжатую на x1 = 6 см, дополнительно сжать на Δx= 8 см?
- Найти приращение энтропии углекислого газа массой 8,8 г при расширении газа
- Вагон закатывается на горку по склону, составляющему угол 30 с горизонтом. Величина силы трения равняется 10% от

