
Непрерывная случайная величина задана интегральной функцией распределения 𝐹(𝑥). Требуется 1) найти дифференциальную функцию
 |
 |
Математический анализ |
 |
 |
Решение задачи |
 |
 |
|
 |
 |
Выполнен, номер заказа №16309 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
|
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл! |
|
Закажите у меня новую работу, просто написав мне в чат! |
Непрерывная случайная величина задана интегральной функцией распределения 𝐹(𝑥). Требуется 1) найти дифференциальную функцию распределения 𝑓(𝑥) (плотность вероятности); 2) построить графики интегральной и дифференциальной функций распределения; 3) найти вероятность попадания значений случайной величины 𝑋 в заданный интервал 𝑃(𝛼 < 𝑋 < 𝛽); 4) вычислить числовые характеристики 𝑀(𝑋), 𝐷(𝑋), 𝜎(𝑋).
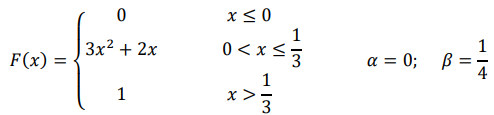
Решение
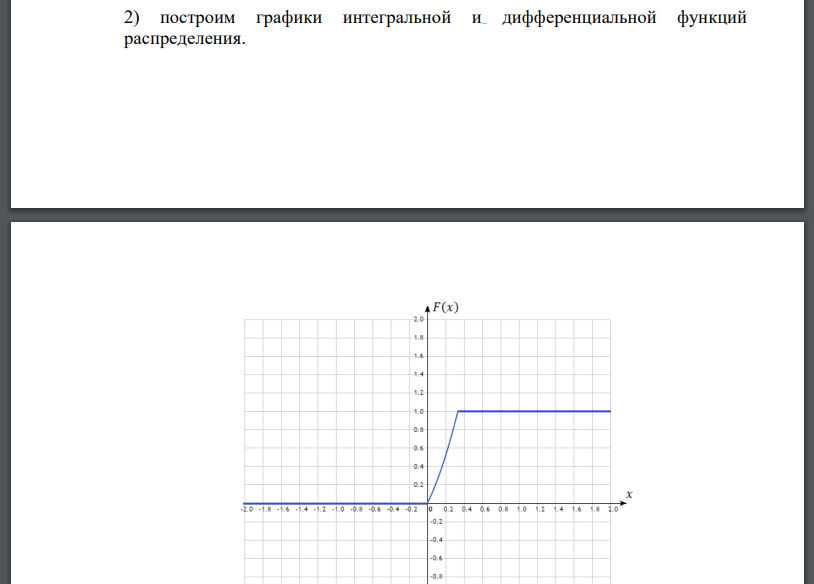
1)) найдем дифференциальную функцию (плотность распределения) 𝑓(𝑥). построим графики интегральной и дифференциальной функций распределения. 3) Вероятность попадания случайной величины в интервал (0; 1 4 ) равна приращению функции распределения на этом интервале: 4) вычислим числовые характеристики 𝑀(𝑋), 𝐷(𝑋), 𝜎(𝑋).

- Один игральный кубик имеет на гранях цифры от одного до шести, а на другом три пары граней помечены цифрами 1, 3, 6. Случайная величина
- Найти математическое ожидание и дисперсию абсолютной разности между выпавшими очками на двух одновременно брошенных
- Охотник, имеющий 6 патронов, стреляет в цель до первого попадания. Вероятность попадания при каждом выстреле равна
- При изготовлении партии одинаковых деталей размером 𝑙 = 20 мм существует допуск ±0,1 мм. Оценить вероятность того

