
На 9 карточках написаны цифры от 0 до 8. Наугад выбирают две карточки одну за другой и укладывают на столе
 |
 |
Математика |
 |
 |
Решение задачи |
 |
 |
|
 |
 |
Выполнен, номер заказа №16082 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
|
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл! |
|
Закажите у меня новую работу, просто написав мне в чат! |
На 9 карточках написаны цифры от 0 до 8. Наугад выбирают две карточки одну за другой и укладывают на столе в порядке появления. Затем читается полученное двузначное число. Какова вероятность того, что оно окажется четным? что оно делится на 3? что оно совпало с задуманным?
Решение
Поскольку не указано иное, полагаем возможным цифру 0 на первом месте двузначного числа. Тогда, например, комбинацию «06» считаем двузначным четным числом, кратным трем. По классическому определению вероятности, вероятность события 𝐴 равна где 𝑚 – число благоприятных исходов, 𝑛 – общее число исходов. Найдем общее число двузначных чисел по формуле размещения без повторения: Основное событие 𝐴 – полученное двузначное число окажется четным. Для четного числа на второй позиции должна быть одна из 5 четных цифр, на первой позиции числа – любая из 8 оставшихся цифр. По правилу умножения: Основное событие 𝐵 – полученное двузначное число делится на 3. Выберем все пары цифр, сумма которых кратна 3: Учитывая, что цифры в числе могут меняться местами, получим: Тогда Основное событие 𝐶 – совпало с задуманным. Учитывая, что задуманное число одно: Тогда Ответ: 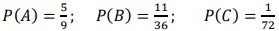

- Дифференциальная функция 𝑓(𝑥) случайной величины задана графиком: Найти: а) аналитическое выражен
- СВ X распределена по закону «прямоугольного треугольника» в интервале (0; a) Найти: 1. Параметр k 2. Аналитич
- Дифференциальная функция распределения случайной величины имеет вид f(x)=Ag(x). Найти параметр А, М(х)
- Найти вероятность получения двузначного числа из цифр 0, 1, 2, 3, 4, 5, 6. Задание

