Кривая распределения случайной величины 𝑋 представляет собой полуэллипс. Найти: 1) величину 𝑏; 2) функци

		Математический анализ
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16310
		Прошла проверку преподавателем МГУ
		245 руб.

Кривая распределения случайной величины 𝑋 представляет собой полуэллипс. Найти: 1) величину 𝑏; 2) функцию плотности вероятности 𝑓(𝑥) и функцию распределения 𝐹(𝑥); 3) построить график функции 𝐹(𝑥).

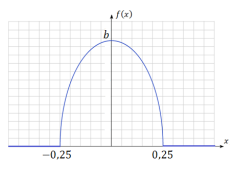
Решение

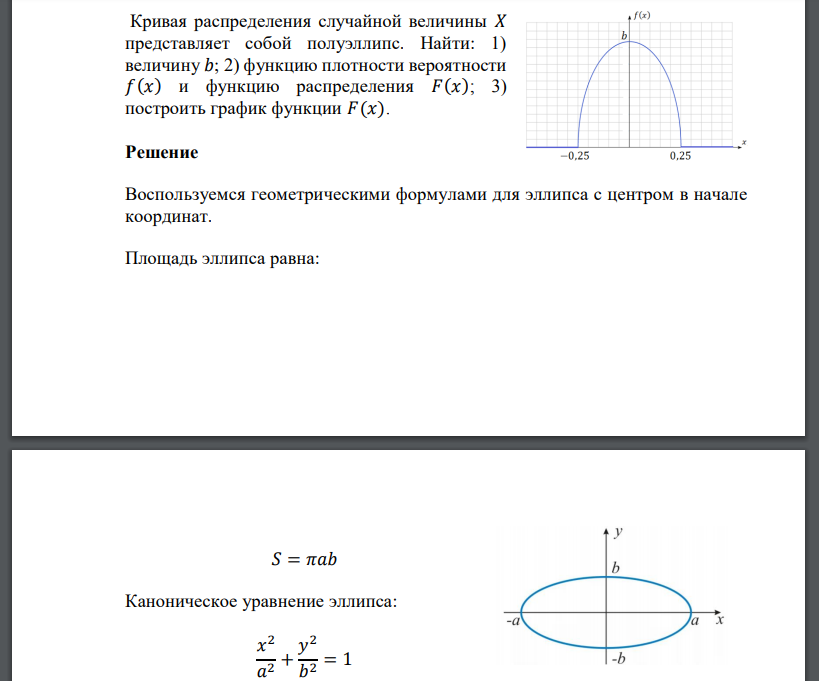
Воспользуемся геометрическими формулами для эллипса с центром в начале координат. Площадь эллипса равна: Каноническое уравнение эллипса: Величину 𝑏 найдем по свойству функции плотности вероятности: Для данного случая получим  Поскольку определенный интеграл в левой части равенства – это площадь заданного полуэллипса, то: 1 При 𝑎 = 0,25 (из рисунка) получим:  Найдем функцию плотности вероятности 𝑓(𝑥). При  запишем уравнение эллипса:  Выше горизонтальной оси 𝑂𝑥 получим 𝑦 ≥ 0, тогда  Таким образом, заданную графически функцию плотности распределения запишем аналитически в виде: 𝑓(𝑥) = { 0, при  при  при 𝑥 > 0,25 Найдем функцию распределения 𝐹(𝑥). По свойствам функции распределения: При  Воспользуемся заменой  тогда . При 𝑡 = −0,25 получим 𝑦 = получим 𝑦 = 𝑎𝑟𝑐𝑠𝑖𝑛(4𝑥). Тогда 8  Преобразуем выражение: 1 1 Тогда функция распределения имеет видпри − Построим график функции 𝐹(𝑥):