
Из урны, содержащей 4 белых и 3 красных шаров, наудачу последовательно и без возвращения извлекаются два шара
 |
 |
Математика |
 |
 |
Решение задачи |
 |
 |
|
 |
 |
Выполнен, номер заказа №16082 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
|
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл! |
|
Закажите у меня новую работу, просто написав мне в чат! |
Из урны, содержащей 4 белых и 3 красных шаров, наудачу последовательно и без возвращения извлекаются два шара. События А={первый шар белый}, С={по крайней мере один из вынутых белый}. Вычислить Р(А/С).
Решение
Найдем вероятность события А – первый шар белый. По классическому определению вероятности, вероятность события А равна где m – число благоприятных исходов, n – общее число исходов. Тогда Найдем вероятность события C – по крайней мере один из вынутых белый. По формуле условной вероятности: Событие 𝐴𝐶 − первый шар был белым при условии что по крайней мере один из вынутых белый возможно в двух случаях – оба шара белые, или первый шар был белым, а второй – черным. Ответ: 𝑃(𝐴/𝐶) = 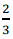

- Известно, что зажигалка не срабатывает в среднем 1 раз из 20. Найти вероятность того, что из 7 зажиганий
- Дана выборка из генеральной совокупности объема. По выборке необходимо выполнить следующие расчеты 5,83 6,91 10,25 10,48 10,16 8,60 8,53 8,00 11,54 7,98 5,10 8,59 10,70 12,29 8,14 9,75 6,99 11,74
- В студенческой группе наудачу выбирают 5 студентов и узнают у них месяц рождения. Рассматриваются события: А = {никакие
- О двух акциях А и В известно, что они выпущены одной и той же отраслью. Вероятность того, что акция А поднимется в цене

