Из 2500 пациентов районной поликлиники по схеме собственно-случайной бесповторной выборки отобрано 220 человек для получения информации о

		Математическая статистика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16423
		Прошла проверку преподавателем МГУ
		245 руб.

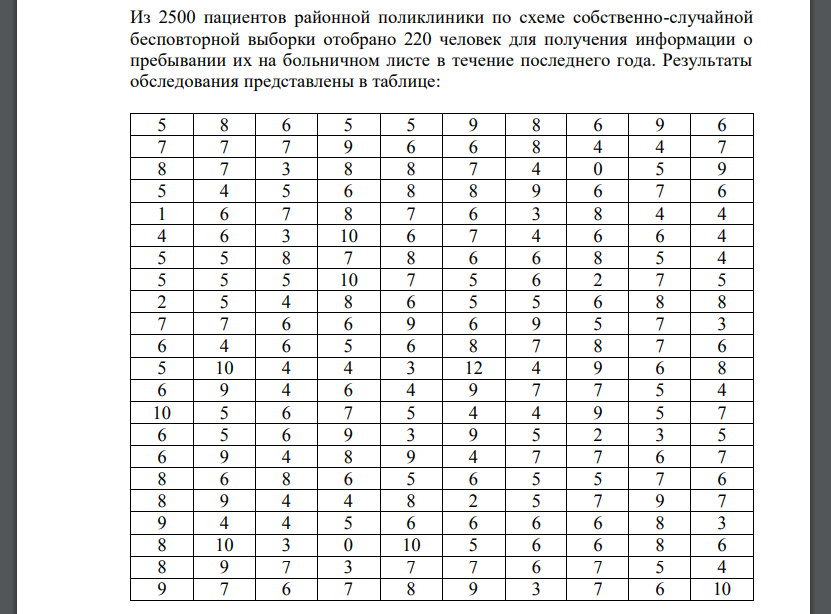
Из 2500 пациентов районной поликлиники по схеме собственно-случайной бесповторной выборки отобрано 220 человек для получения информации о пребывании их на больничном листе в течение последнего года. Результаты обследования представлены в таблице:

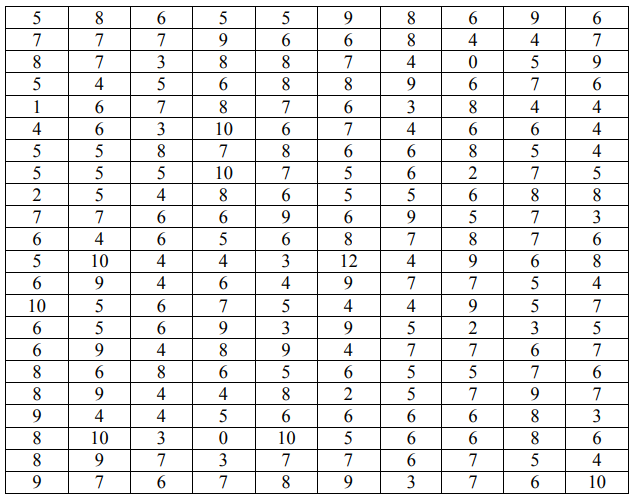
1. Составить интервальный вариационный ряд. Построить гистограмму и полигон частот (на одном графике), эмпирическую функцию распределения (кумуляту). 2. По сгруппированным данным вычислить выборочные числовые характеристики: среднее арифметическое, исправленную выборочную дисперсию, среднее квадратическое отклонение, коэффициент вариации, асимметрию, эксцесс, моду и медиану. 3. Используя 𝜒 2 -критерий Пирсона, на уровне значимости 𝛼 = 0,05 проверить гипотезу о том, что случайная величина 𝜉 – время пребывания на больничном листе – распределена по нормальному закону. Построить на чертеже, содержащем гистограмму эмпирического распределения, соответствующую нормальную кривую. 4. Предположив нормальность распределения времени пребывания пациентов на больничном листе, на 5%-ном уровне значимости проверить следующие гипотезы: а) о числовом значении математического ожидания, приняв в качестве нулевой гипотезы 𝐻0: 𝑎 = 𝑎0, где 𝑎0 – средняя арифметическая, при альтернативной гипотезе 𝐻1: 𝑎 ≠ 𝑎0; б) о числовом значении дисперсии, приняв в качестве нулевой гипотезы 𝐻0: 𝜎 2 = 𝜎0 2 , где в качестве 𝜎0 2 взять исправленную выборочную дисперсию, при альтернативной гипотезе 𝐻1: 𝜎 2 < 𝜎0 2 ; в) о числовом значении вероятности события, состоящего в том, что время пребывания на больничном листе составляет не менее 8 дней, приняв в качестве нулевой гипотезы 𝐻0: 𝑝 = 𝑝0 = 𝜔, где 𝜔 – соответствующая выборочная доля, вычисленная по не сгруппированным данным, при альтернативной гипотезе 𝐻1: 𝑝 > 𝑝0. 5. Предположив нормальность распределения времени пребывания на больничном листе, требуется: а) построить 95%-ные интервальные оценки математического ожидания, дисперсии, среднего квадратичного отклонения и вероятности события, рассмотренного в п. 4в; б) определить вероятности 𝛾 того, что генеральная средняя и генеральная доля, рассмотренная в п. 4в, отличаются от соответствующих им выборочных числовых характеристик не более чем на 5% т.е. оцениваемый параметр генеральной совокупности 𝑡 накрывается интервалом (0,95𝜃; 1,05𝜃), где 𝜃 – соответствующая выборочная оценка; в) определить объемы выборок, чтобы те же границы для генеральной средней и генеральной доли (п. 5б), гарантировать с вероятностями, большими, чем полученные в п. 5б, на 50% от (1 − 𝛾).

Решение

1. Построим выборку в порядке возрастания: Поскольку все значения в выборке целые, целесообразно взять шаг интервала 1 и число интервалов 13. Подсчитаем частоту каждого интервала, то есть число вариант, попавших в этот интервал. Варианты, совпадающие с границами частичных интервалов, включают в правый интервал. Относительные частоты 𝑚∗ определим по формуле:  Запишем в виде таблицы интервальный вариационный ряд. Номер интервала Интервал Середина интервала Частота 𝑚 Относительная частота  Построим на одном графике гистограмму (синим цветом) и полигон (черным цветом) частот.