Используя ретроспективные данные за 6 лет, спрогнозируйте объем производства продукции на следующие 3 года при условии сохранения тенденций функционирования бизнеса

		Экономика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №17370
		Прошла проверку преподавателем МГУ
		245 руб.

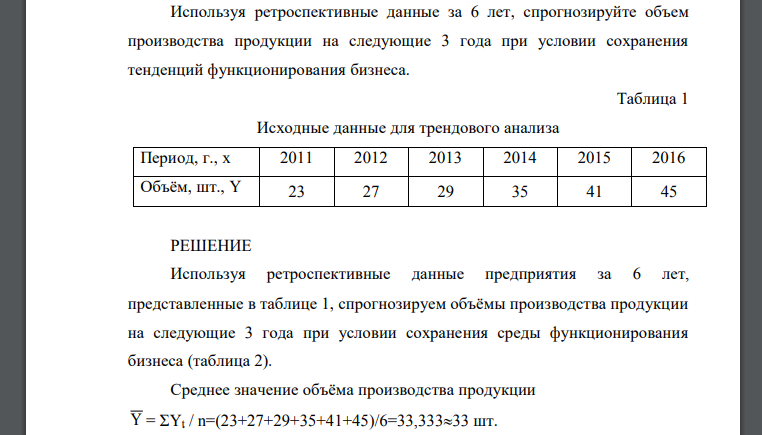
Используя ретроспективные данные за 6 лет, спрогнозируйте объем производства продукции на следующие 3 года при условии сохранения тенденций функционирования бизнеса.

РЕШЕНИЕ

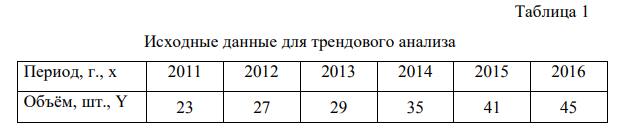
Используя ретроспективные данные предприятия за 6 лет, представленные в таблице 1, спрогнозируем объёмы производства продукции на следующие 3 года при условии сохранения среды функционирования бизнеса (таблица 2). Среднее значение объёма производства продукции

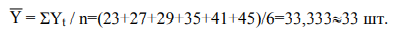
Расчёт среднего объёма производства продукции показывает, что в каждый период (год) предприятие производило в среднем 33 единицы продукции. Значение объёма производства в динамике увеличивается. Зависимость между объёмом производства продукции и периодом времени показана на рисунке 2.

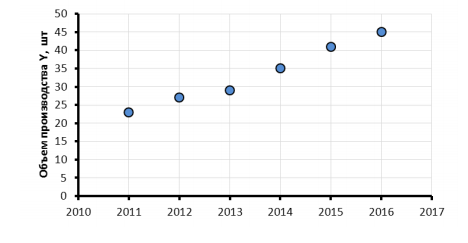
Рисунок 1. – Динамика производства продукции Если связь между факторным и результативным показателями носит прямолинейный характер, то уравнения парной регрессии имеют вид:

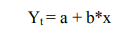
где а – свободный член уравнения при х = 0 x – фактор, определяющие уровень изучаемого результативного показателя (независимый параметр); b – коэффициент регрессии при факторном показателе; он характеризуют уровень влияния фактора на результативный показатель в абсолютном выражении. Показатели а и b следует отыскать. Значение коэффициентов a и b находят из системы уравнений, полученных по способу наименьших квадратов (x = t):

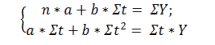
где n – число наблюдения (в нашем примере – это 7 лет); t – независимый параметр Y – объём производства продукции. Значения Σt, ΣY, 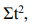 ΣtY рассчитываются на основании фактических исходных данных; результаты расчётов представлены в таблице 2.

Таблица 2 – Расчёт показателей трендовой модели для прогноза объёма производства продукции

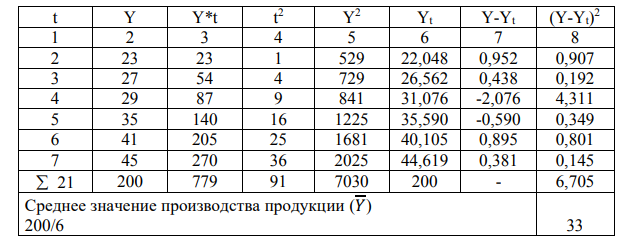
Среднее значение производства продукции

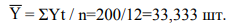
Определим коэффициенты уравнения:

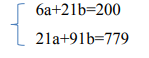
Из первого уравнения: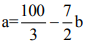 

Подставим во второе:

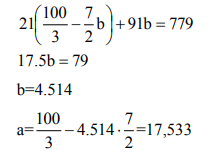
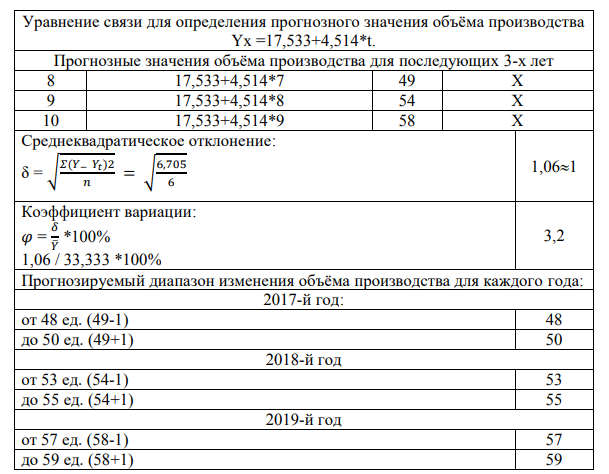
Уравнение связи для определения прогнозного значения объёма производства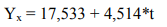  

Если в уравнение регрессии Yx = 17,533+4,514*t подставить соответствующее значение t, то можно рассчитать прогнозируемое значение объёма производства (Yx) для каждого ретроспективного квартала и последующего квартала (столбец 6).

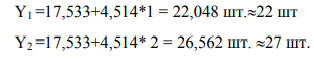
Прогноз:

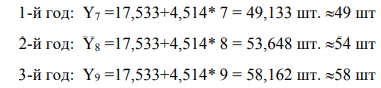
В колонках 7,8 рассчитаны отклонения фактического уровня производства продукции от расчётного для каждого ретроспективного и прогнозного периода. Для оценки качества данных, определения диапазона изменения прогнозируемого объёма производства в каждый квартал рассчитаем среднее квадратическое отклонение прогнозируемого показателя и коэффициент вариации по формулам: Среднеквадратическое отклонение:

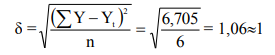
коэффициент вариации:

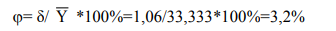
В таблице 2 показаны алгоритм и результаты расчётов этих показателей. В данном случае среднеквадратическое отклонение составило 1 шт. С учётом этого показателя можно указан прогнозируемый диапазон изменения объёма производства для каждого из трех лет, начиная с 7-го. Результаты расчётов показали, что прогнозируемый диапазон объёма производства составит

для 2017-го года – от 48 шт. до 50 шт.;

для 2018-го года – от 53 шт. до 55 шт.;

для 2019-го года – от 57 шт. до 59шт.

Значение коэффициента вариации в данном случае составило 3,2%, что означает слабую колеблемость анализируемого признака. Так как разброс значений вокруг среднего незначительный, риск бизнеса производства продукции низкий.