Эмпирическое распределение задано в виде последовательности равноотстоящих вариант и соответствующих им частот
 |
 |
Математическая статистика |
 |
 |
Решение задачи |
 |
 |
|
 |
 |
Выполнен, номер заказа №16457 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
|
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл! |
|
Закажите у меня новую работу, просто написав мне в чат! |
Эмпирическое распределение задано в виде последовательности равноотстоящих вариант и соответствующих им частот
Найти распределение относительных частот. Найти эмпирическую функцию распределения. Построить полигон частот. Найти выборочную среднюю, выборочную несмещенную дисперсию, выборочное среднее квадратическое отклонение. Оценить с помощью критерия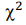 
гипотезу о согласии выборочного распределения с законом нормального распределения при уровне значимости 
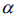= 0,01.
Решение
Относительные частоты определим по формуле: где 𝑛 − объём выборки, то есть число единиц наблюдения. Найдем эмпирическую функцию распределения. Построим полигон частот. Найдем выборочное среднее (оценка математического ожидания): Выборочная дисперсия: Несмещенная (исправленная) оценка генеральной дисперсии Выборочное среднее квадратическое отклонение Оценим с помощью критерия 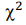гипотезу о согласии выборочного распределения с законом нормального распределения при уровне значимости Теоретические частоты определим по формуле: Сравним эмпирические и теоретические частоты. Составим расчетную таблицу, из которой найдем наблюдаемое значение критерия Число степеней свободы По таблице при уровне значимости находим Так как то на данном уровне значимости гипотеза о нормальном распределении принимается.
Похожие готовые решения по математической статистике:
- Даны выборка в виде таблицы и число 𝑚 = 13. Построить полигон частот. Найти оценку математического ожидания, несмещенную
- Эмпирическое распределение задано в виде последовательности равноотстоящих вариант и соответствующих им частот 𝑥𝑖 2,5 7,5 12,5 17,5 22,5 𝑚𝑖 15 75 100 50 20 Найти
- Эмпирическое распределение задано в виде последовательности равноотстоящих вариант и соответствующих им частот 𝑥𝑖 2,6 3,0 3,4 3,8 4,2 𝑚𝑖 8 20 45 15 12 Найти
- Дискретный вариационный ряд имеет вид: 𝑥𝑖 5 12 24 30 36 𝑛𝑖 3 5 8 6 3 Пусть 𝐹̂(𝑥) – эмпирическая функция распределения. Найти
- По заданной таблице частот требуется: найти и построить эмпирическую функцию распределения; найти выборочную среднюю
- Выборочная совокупность задана таблицей распределения: 𝑥𝑖 1 2 5 8 9 𝑛𝑖 3 4 6 4 3 Найти выборочную среднюю, выборочную
- Построить полигон частот. Найти оценку математического ожидания, несмещенную оценку дисперсии, точность оценки
- Выборка (объем выборки 20) задана в виде частот распределения. Построить полигон относительных частот. Найти выборочное среднее
- Расстояние между пластинами плоского воздушного конденсатора уменьшили в 2 раза. Найдите, во сколько раз
- Конденсаторы емкостями 1 и 6 нФ соединены параллельно. Заряд первого конденсатора 10 мкКл. Определить заряд второго конденсатора
- Какую работу нужно совершить, чтобы удалить слюдяную пластинку из плоского конденсатора
- Конденсаторы емкостями 1С=1 мкФ, 2С=2 мкФ и 3С=3 мкФ образуют цепь, показанную на рисунке. Разность потенциалов