Автор Анна Евкова
Преподаватель который помогает студентам и школьникам в учёбе.

Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1

Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1 Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1 Высшая математика
Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1 Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1 Решение задачи
Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1 Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1
Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1 Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1 Выполнен, номер заказа №16173
Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1 Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1 Прошла проверку преподавателем МГУ
Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1 Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1  245 руб. 

Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1

Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!

Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1

Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):

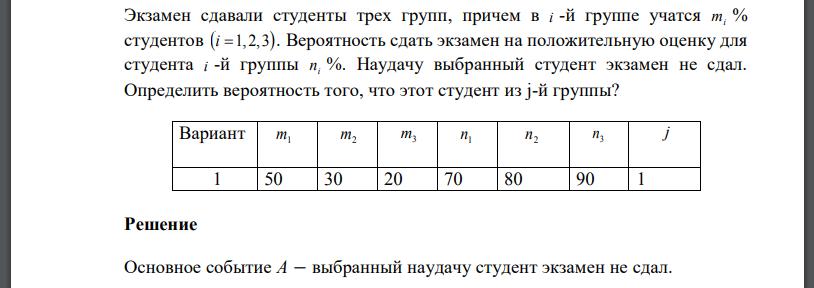
Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Наудачу выбранный студент экзамен не сдал. Определить вероятность того, что этот студент из j-й группы? 

Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1

Решение

Основное событие А − выбранный наудачу студент экзамен не сдал. Гипотезы: 𝐻1 − этот студент из первой группы; 𝐻2 − этот студент из второй группы; 𝐻3 − этот студент из третьей группы. Вероятности гипотез (по классическому определению вероятности): Условные вероятности: Вероятность того, что не сдавший экзамен студент – это студент из первой группы, по формуле Байеса:  Ответ: 𝑃(𝐻1|𝐴) = 0,65

Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1

Экзамен сдавали студенты трех групп, причем в i -й группе учатся mi % студентов i  1, 2,3 . Вероятность сдать экзамен на положительную оценку для студента i -й группы i n %. Вариант 1