Для изучения некоторого количественного признака 𝑋 генеральной совокупности получена выборка. Необходимо 16 13 11 15 18 19 21 18 11 15 14 16 18 17 21 22 13 12 15

		Теория вероятностей
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16412
		Прошла проверку преподавателем МГУ
		245 руб.

Для изучения некоторого количественного признака 𝑋 генеральной совокупности получена выборка. Необходимо: 1) задать статистическое распределение выборки в виде интервальной таблицы частот и интервальной таблицы относительных частот; 2) построить гистограмму частот; 3) найти выборочную среднюю, выборочную дисперсию и исправленную выборочную дисперсию, выборочное среднее квадратическое отклонение и исправленное выборочное среднее квадратическое отклонение. 16 13 11 15 18 19 21 18 11 15 14 16 18 17 21 22 13 12 15 16 17 20 17 17 20 20 18 22 23 13 15 10 10 12 12 18 18 19 21 23 20 22 23 17 16 14 15 18 15 11 16 17 15 13 16 17 18 14 15 20

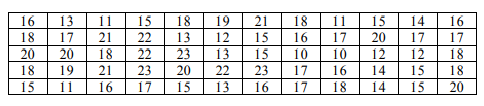
Решение

Зададим статистическое распределение выборки в виде интервальной таблицы частот и интервальной таблицы относительных частот. Построим вариационный ряд – выборку в порядке возрастания:  Найдем размах выборки  Число интервалов 𝑁, на которые следует разбить интервал значений признака, найдём по формуле Стерджесса:  объём выборки, то есть число единиц наблюдения. В данном случае. Получим:  Рассчитаем шаг (длину частичного интервала) ℎ по формуле:  Округление шага производится, как правило, в большую сторону. Таким образом, принимаем . За начало первого интервала принимаем такое значение из интервала чтобы середина полученного интервала оказалась удобным для расчетов числом. В данном случае за нижнюю границу интервала возьмём 9,5. В результате получим следующие границы интервалов: Подсчитаем частоту 𝑛𝑖 каждого интервала, то есть число вариант, попавших в этот интервал. Варианты, совпадающие с границами частичных интервалов, включают в левый интервал. Относительные частоты (частости) 𝑓𝑖 определим по формуле: Номер интервала Интервал Середина интервала Частота 𝑛𝑖 Относительная частота 2) Построим гистограмму частот. 3) Найдем выборочную среднюю, выборочную дисперсию и исправленную выборочную дисперсию, выборочное среднее квадратическое отклонение и исправленное выборочное среднее квадратическое отклонение. Выборочная средняя:  Несмещенная (исправленная) дисперсия: Выборочное среднее квадратическое отклонение  Исправленное среднеквадратичное отклонение