Дифференциальная функция 𝑓(𝑥) случайной величины задана графиком: Найти: а) аналитическое выражен

		Математический анализ
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16310
		Прошла проверку преподавателем МГУ
		245 руб.

Дифференциальная функция 𝑓(𝑥) случайной величины задана графиком: Найти: а) аналитическое выражение 𝑓(𝑥); б) функцию распределения 𝐹(𝑥) и ее график; в) вероятность 𝑃(0,5 < 𝑥 < 3); г) основные характеристики; д) вероятность того, что при трех испытаниях она примет значение больше 1.

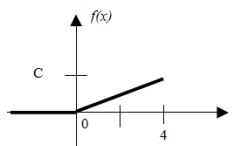
Решение

а) По графику функции плотности вероятности запишем ее аналитическое выражение:  при  при  Значение параметра 𝑐 находим из условия: Откуда  Тогда плотность вероятностей имеет вид: По свойствам функции распределения: При Тогда функция распределения 𝐹(𝑥) имеет вид:  Найдем вероятность попадания случайной величины Х в интервал (0,5; 3), которая равна приращению функции распределения на этом интервале:  64 г) Найдем математическое ожидание 𝑀(𝑋), дисперсию 𝐷(𝑋) и среднее квадратическое отклонение 𝜎(𝑋) случайной величины  вероятность того, что при одном испытании случайная величина примет значение больше 1, равна:  Найдем вероятность того, что при трех испытаниях случайная величина примет значение больше 1. Воспользуемся формулой Бернулли. Если производится 𝑛 независимых испытаний, при каждом из которых вероятность осуществления события 𝐴 постоянна и равна 𝑝, а вероятность противоположного события равна 𝑞 = 1 − 𝑝, то вероятность того, что при этом событие 𝐴 осуществляется ровно 𝑚 раз, вычисляется по формуле  число сочетаний из 𝑛 элементов по 𝑚. Для данного случая