Автор Анна Евкова
Преподаватель который помогает студентам и школьникам в учёбе.

Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения,

Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения, Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения, Математическая статистика
Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения, Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения, Решение задачи
Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения, Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения,
Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения, Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения, Выполнен, номер заказа №16428
Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения, Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения, Прошла проверку преподавателем МГУ
Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения, Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения,  245 руб. 

Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения,

Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!

Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения,

Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):

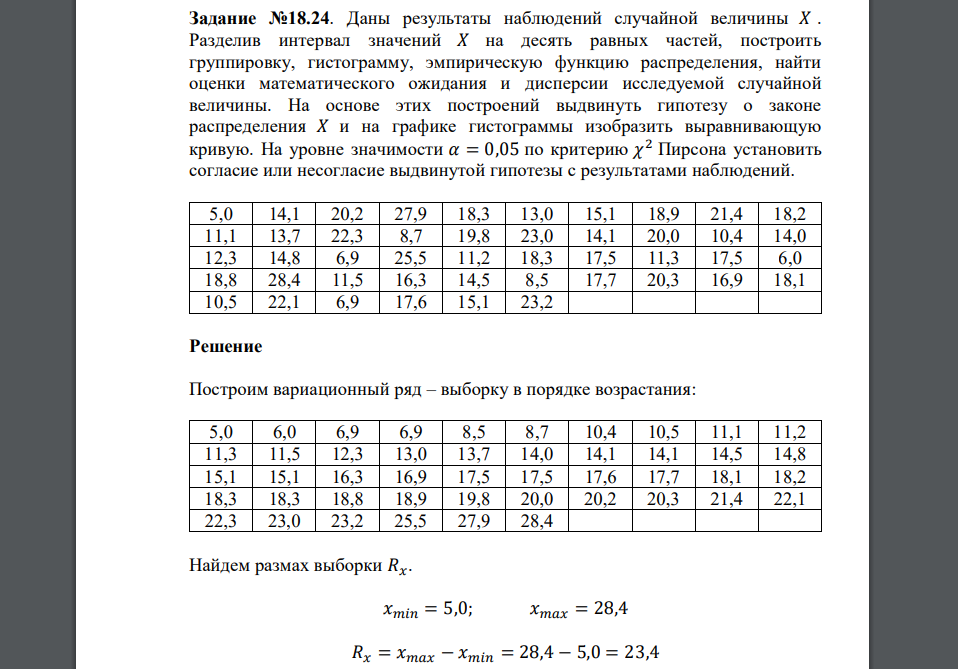
Задание №18.24. Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения, найти оценки математического ожидания и дисперсии исследуемой случайной величины. На основе этих построений выдвинуть гипотезу о законе распределения 𝑋 и на графике гистограммы изобразить выравнивающую кривую. На уровне значимости 𝛼 = 0,05 по критерию 𝜒 2 Пирсона установить согласие или несогласие выдвинутой гипотезы с результатами наблюдений. 5,0 14,1 20,2 27,9 18,3 13,0 15,1 18,9 21,4 18,2 11,1 13,7 22,3 8,7 19,8 23,0 14,1 20,0 10,4 14,0 12,3 14,8 6,9 25,5 11,2 18,3 17,5 11,3 17,5 6,0 18,8 28,4 11,5 16,3 14,5 8,5 17,7 20,3 16,9 18,1 10,5 22,1 6,9 17,6 15,1 23,2

Решение

Построим вариационный ряд – выборку в порядке возрастания:  Найдем размах выборки  Число интервалов 𝑁, на которые следует разбить интервал значений признака, заданы в условии: 𝑁 = 10 Рассчитаем шаг (длину частичного интервала) ℎ по формуле:  Подсчитаем частоту каждого интервала, то есть число вариант, попавших в этот интервал. Варианты, совпадающие с границами частичных интервалов, включают в правый интервал. Относительные частоты 𝜔 определим по формуле:  Плотность относительной частоты для каждого интервала вычислим по формуле: Номер интервала Интервал Середина интервала Частота 𝑛𝑖 Относительная частота  Построим гистограмму относительных частот. Эмпирическая функция распределения Построим график эмпирической функции распределения. Найдем выборочную среднюю 𝑥̅в и выборочную дисперсию  Найдем несмещенную оценку дисперсии Исправленное среднее квадратическое отклонение равно: По виду гистограммы, построенной равноинтервальным способом, выдвинем гипотезу о нормальном законе распределения. Плотность распределения вероятности нормально распределенной случайной величины имеет вид  получим аналитическую запись для плотности вероятности и построим на графике гистограммы выравнивающую кривую:  Проверим выдвинутую гипотезу о законе распределения случайной величины с помощью критерия согласия Пирсона при уровне значимости 0,05. Вероятность попадания случайной величины в каждый интервал равна приращению функции распределения:Теоретические частоты определим по формуле 𝑛𝑖 ′ = 𝑛 ∙ 𝑝𝑖 и вычислим значения Результаты запишем в таблицу Интервал Здесь объединены первые два и последние три интервала, чтобы выполнялось условие 𝑛 ∙ 𝑝𝑖 > 5 . В итоге получили 𝑚 = 7 интервалов, число степеней свободы для 𝜒 2 распределения равно  По таблице при уровне значимости находим  Так как то при заданном уровне значимости гипотеза о нормальном распределении принимается

Даны результаты наблюдений случайной величины 𝑋 . Разделив интервал значений 𝑋 на десять равных частей, построить группировку, гистограмму, эмпирическую функцию распределения,