Даны две случайные величины Х и Y, причем Х имеет биномиальное распределение с параметрами p = 0,2 и n = 5, а Y – распределение

		Математическая статистика
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16457
		Прошла проверку преподавателем МГУ
		245 руб.

Даны две случайные величины Х и Y, причем Х имеет биномиальное распределение с параметрами p = 0,2 и n = 5, а Y – распределение Пуассона с параметром 𝜆 = 0,5 . Пусть Z = 2X – Y. Необходимо: а) найти математическое ожидание M(Z) и дисперсию D(Z); б) оценить вероятность P (1 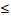Z 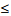2) с помощью неравенства Чебышева.

Решение

Для биномиального распределения справедливы формулы: Математическое ожидание 𝑀(𝑋) равно: Дисперсия 𝐷(𝑋) равна: По условию Тогда  Для показательного закона:  а) найдем математическое ожидание M(Z) и дисперсию D(Z). Воспользуемся следующими свойствами математического ожидания: Математическое ожидание алгебраической суммы конечного числа случайных величин равно сумме их математических ожиданий: Постоянный множитель можно выносить за знак математического ожидания:  Тогда искомое математическое ожидание случайной величины  равно:  Воспользуемся следующими свойствами дисперсии: Дисперсия алгебраической суммы конечного числа независимых случайных величин равна сумме их дисперсий:  Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат: Тогда искомая дисперсия случайной величины  равна:  б) оценим вероятность с помощью неравенства Чебышева. Неравенство Чебышева утверждает, что каково бы ни было положительное число 𝜀, вероятность того, что величина 𝑍 отклонится от своего математического ожидания не меньше, чем на 𝜀, ограничена сверху величиной Очевидно, что при  неравенство Чебышева не дает возможности объективно оценить искомую вероятность.