Дана зависимость составов жидкой (x) и газообразной (у) фаз от температуры (Т) для бинарной жидкой системы А - В при постоянном давлении р

		Химия
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16852
		Прошла проверку преподавателем МГУ
		245 руб.

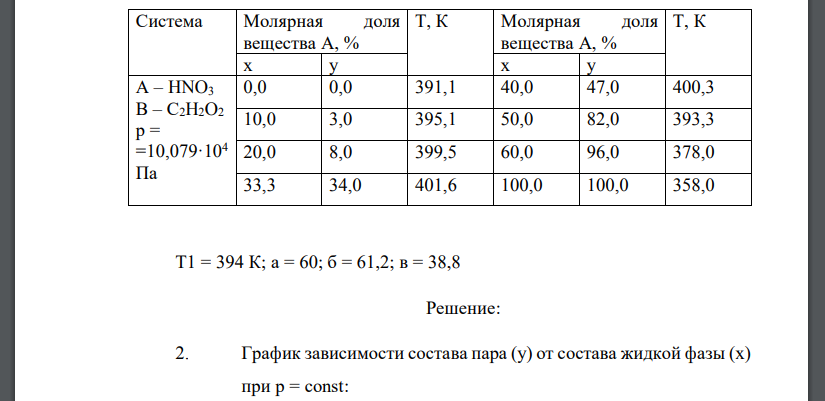
Дана зависимость составов жидкой (x) и газообразной (у) фаз от температуры (Т) для бинарной жидкой системы А - В при постоянном давлении р. Составы х и у приведены в молярных долях вещества А, выраженных в процентах (данные по вариантам приведены в таблице ниже). 1. Построить график зависимости состава пара (у) от состава жидкой фазы (х) при р = const. 2. Построить график зависимости состав - температура кипения. 3. Определить: температуру кипения системы, в которой молярная доля компонента А равна а %; каков состав первого пузырька пара; при какой температуре исчезнет последняя капля жидкости и каков ее состав. 4. Определить состав пара, находящегося в равновесии с жидкой бинарной системой, кипящей при температуре Т1. 5. При помощи какого эксперимента можно установить состав жидкой бинарной системы, если она начинает кипеть при температуре Т1 (при наличии диаграммы состав - температура кипения)? 6. Какой компонент может быть выделен из системы, состоят из б кг вещества А и в кг вещества В, и какова масса выделенного компонента? 7. Какого компонента и сколько его надо добавить к указанной в п. 6 смеси, чтобы получилась азеотропная смесь? 8. Сколько вещества А (кг) будет в парах и в жидкой фазе, если 2 кг смеси, содержащей а % вещества А, нагреть до температуры Т1? 9. Определить вариантность системы в азеотропной точке. Система Молярная доля вещества А, % Т, К Молярная доля вещества А, % Т, К х у х у А – HNO3 В – С2H2O2 р = =10,079·104 Па 0,0 0,0 391,1 40,0 47,0 400,3 10,0 3,0 395,1 50,0 82,0 393,3 20,0 8,0 399,5 60,0 96,0 378,0 33,3 34,0 401,6 100,0 100,0 358,0 Т1 = 394 К; а = 60; б = 61,2; в = 38,8

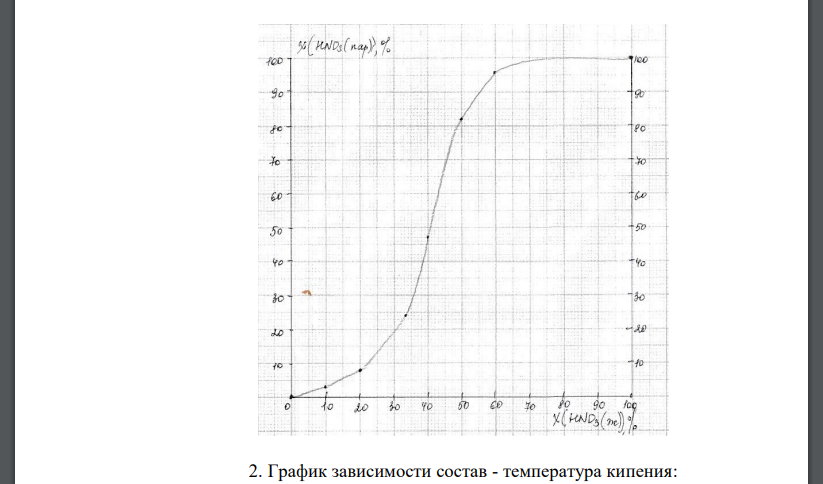
Решение: 2. График зависимости состава пара () от состава жидкой фазы () при . График зависимости состав - температура кипения: 3. Температура кипения системы, содержащей  равна . Состав первого пузырька пара: . Последняя капля жидкости исчезнет при , ее состав  и . 4. Определим состав пара, находящегося в равновесии с жидкой бинарной системой, кипящей при температуре  и  и  и . Состав жидкой бинарной системы, если она начинает кипеть при температуре  можно установить при помощи следующего эксперимента. К исходной смеси необходимо добавить какой-нибудь из компонентов, например, компонент , и снова измерить температуру кипения. Если  увеличится по сравнению с , значит система содержала недостаток  по сравнению с азеотропной смесью и ее состав определяем по левой части диаграммы. В противном случае - содержала недостаток  и состав определяется по правой части диаграммы. 6. Определим, какой компонент может быть выделен из системы, состоящей из  вещества  и  вещества , и массу выделенного компонента. Для этого рассчитаем мольные доли компонентов.  Азеотропная смесь имеет состав  и . Так как заданный состав находится справа от азеотропной точки, то выделить ректификацией в чистом виде можно только . Весь  перейдет в азеотропную смесь с молярным содержанием 67 %. Остальные 33 % в азеотропном растворе составит . Определим количество , перешедшее в азеотроп:  Тогда в чистом виде можно выделить . 7. В п.6 система состоит из  и . Азеотропная смесь имеет состав  и .  в системе находится в недостатке относительно азеотропа, следовательно, к системе необходимо добавлять , чтобы получить из исходной системы азеотропную, содержание азотной кислоты останется без изменений. Определим количество , содержащееся в азеотропе: . Тогда количество , которое необходимо добавить для получения азеотропной смеси, равно . 8. По правилу рычага:  Определим количество молей вещества, которое содержится в системе массой 2 кг. Для этого вычислим среднюю молярную массу смеси:  Найдем химическое количество смеси:  Количество  в парах: . Количество HNO3 в жидкой фазе: . 9. Определим вариантность (число степеней свободы) системы в азеотропной точке при постоянном давлении. Для определения числа степеней свободы используется правило фаз Гиббса, согласно которому  , где – число степеней свободы (вариантность) системы;  – количество компонентов;  – число фаз системы; – число внешних факторов, влияющих на равновесие в данной системе. В данном случае имеем: - система двухкомпонентная , однако в азеотропной точке составы жидкой фазы и пара одинаковы (второй закон Коновалова), т.е. система ведет себя как однокомпонентная, т.е. в азеотропной точке ; - в азеотропной точке в равновесии сосуществуют две фазы – жидкость и пар – , т. к. . Таким образом, вариантность системы в азеотропной точке , т. е. система инвариантна (безвариантна)