Автор Анна Евкова
Преподаватель который помогает студентам и школьникам в учёбе.

Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между

Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между Математическая статистика
Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между Решение задачи
Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между
Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между Выполнен, номер заказа №16472
Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между Прошла проверку преподавателем МГУ
Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между  245 руб. 

Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между

Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!

Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между

Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):

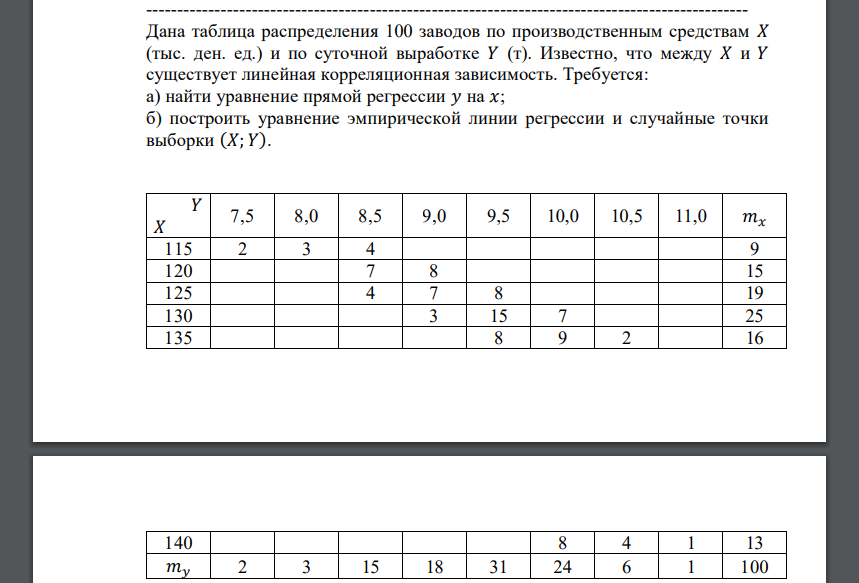
Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между 𝑋 и 𝑌 существует линейная корреляционная зависимость. Требуется: а) найти уравнение прямой регрессии 𝑦 на 𝑥; б) построить уравнение эмпирической линии регрессии и случайные точки выборки (𝑋; 𝑌). 𝑌 𝑋 7,5 8,0 8,5 9,0 9,5 10,0 10,5 11,0 𝑚𝑥 115 2 3 4 9 120 7 8 15 125 4 7 8 19 130 3 15 7 25 135 8 9 2 16 140 8 4 1 13 𝑚𝑦 2 3 15 18 31 24 6 1 100

Решение

а) Выборочные средние:  Дисперсии:  Несмещенные оценки дисперсий: Откуда получаем: Ковариация: Определим коэффициент корреляции: б) Уравнение линейной регрессии с 𝑌 на 𝑋 имеет вид: На чертеже построим уравнение регрессии 𝑌 на 𝑋 и поле корреляции

Дана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что междуДана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что междуДана таблица распределения 100 заводов по производственным средствам 𝑋 (тыс. ден. ед.) и по суточной выработке 𝑌 (т). Известно, что между

Похожие готовые решения по математической статистике: