Дан интервальный статистический ряд распределения частот экспериментальных значений случайной величины Х. Требуется: 1)построить полигон и гистограмму частостей (относительных частот) СВ 2) по виду

		Теория вероятностей
		Решение задачи
		18 февраля 2021
		Выполнен, номер заказа №16393
		Прошла проверку преподавателем МГУ
		245 руб.

Дан интервальный статистический ряд распределения частот экспериментальных значений случайной величины Х. Требуется: 1)построить полигон и гистограмму частостей (относительных частот) СВ 2) по виду полигона и гистограммы и, исходя из механизма образования СВ, сделать предварительный выбор закона распределения; 3) вычислить выборочную среднюю в x и исправленное среднее квадратическое отклонение s; 4) записать гипотетичную функцию распределения и плотность распределения; 5) найти доверительные интервалы для математического ожидания и среднего квадратического отклонения при доверительной вероятности 6) найти теоретические частоты нормального закона распределения и проверить гипотезу о нормальном распределении СВ с помощью критерия Пирсона при уровне значимости 

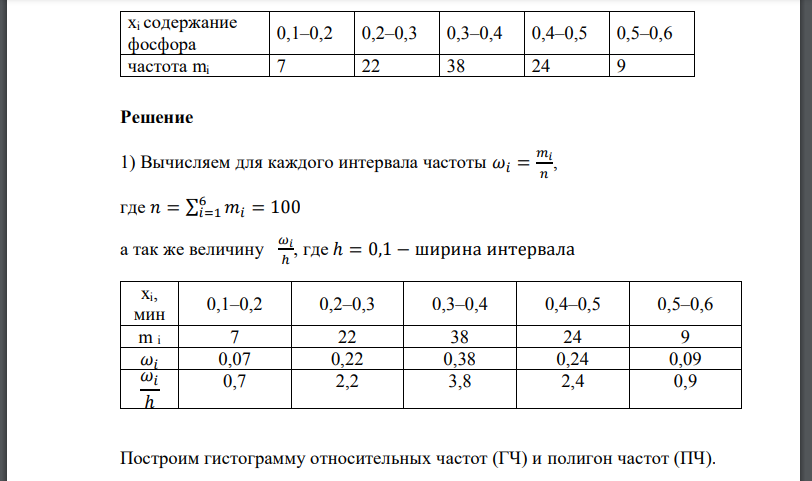
Решение

1) Вычисляем для каждого интервала частоты а так же величину ширина интервала Построим гистограмму относительных частот (ГЧ) и полигон частот (ПЧ). содержание фосфора  частота 2) Так как полигон частот приближенно представляет кривую Гаусса и содержание фосфора зависит от большого числа независимых параметров, то можно сделать предположение о нормальном распределении случайной величины. 3) Выборочная средняя и исправленное среднее квадратическое отклонение равны: 4) Запишем гипотетичную функцию распределения и плотность распределения Плотность распределения вероятности нормально распределенной случайной величины имеет вид При получим  Функция распределения имеет вид где  – функция Лапласа. 5) Найдем доверительные интервалы для математического ожидания и среднего квадратического отклонения при доверительной вероятности Найдем доверительный интервал для математического ожидания Тогда Для записи доверительного интервала для дисперсии, по числу  получим коэффициенты Тогда 6) Найдем теоретические частоты нормального закона распределения и проверим гипотезу о нормальном распределении СВ с помощью критерия Пирсона при уровне значимости  . Вычислим вероятности попаданий СВ в каждый интервал Интервалы Получили Число степеней свободы По таблице при уровне значимости находим Так как то нет оснований отвергать гипотезу о нормальном распределении.