Шаровая поверхность в начертательной геометрии с примером

Шаровая поверхность:

Шаровой поверхностью (или сферой) называется поверхность, образованная при вращении окружности вокруг своего диаметра.

Если шаровая поверхность пересе­кается плоскостью, то в сечении всегда получается окружность. Эта окружность может спроецироваться:

• - в прямую, если секущая плоскость перпендикулярна плоскости проекций;
• - в окружность, если секущая плоскость параллельна плоскости проекций. Например, окружность с радиу­сом
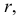
• - в эллипс, если секущая плоскость не параллельна плоскости проекций.

Чтобы построить проекции точки, лежащей на поверхности шара, необходимо через нее провести секущую плоскость, параллельную плоскости проекций, затем построить окружность, на которой находит­ся эта точка.

Пересечение шаровой поверхности плоскостью

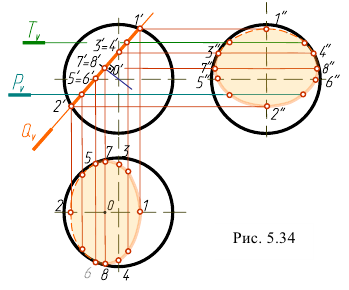
Пересечем поверхность шара фронтально-проецирующей плоскостью (рис. 5.34). Построение начинаем с определения характерных точек. Точки 1 и 2 находятся на главном меридиане. Эти точки - концы малой оси эллипса, а также это самая высокая и самая низкая точки. Их горизонтальные и профильные проекции строим по фронтальным проекциям. Точки 3 и 4 находятся на профильном меридиане и определяют видимость на профильной плоскости проекций. Горизонтальные проекции точек находим по профильным проекциям. Точки 5 и 6 находятся на экваторе и являются точками границы видимости на горизонтальной проекции. Профильные проекции точек находим по горизонтальным проекциям. Точки 7 и 8 принадлежат концам большой оси эллипса. Они строятся следующим образом. Сначала нужно найти фронтальную проекцию точки о’. 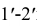Она находится в середине отрезка и является центром окружности сечения. Затем строится ее горизонтальная проекция- точка о. Отрезки 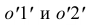на фронтальной проекции равны истинной величине радиуса этой окружности. На гори­зонтальной проекции диаметр окружности изображается без искажения. 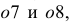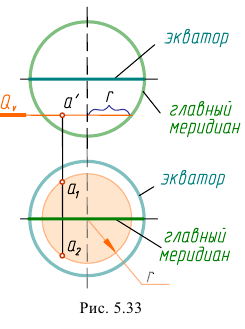Поэтому откладываем отрезки равные 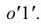Для точного построения линии сечения необходимо найти несколько дополнительных точек. Для их построения используем вспомогательные секущиеся плоскости, как показано на рис. 5.33. Полученные точки соединяем плавной кривой с учетом ее видимости.

Развертка поверхности шара

Сферическая поверхность относится к неразвертываемым поверхностям, и поэтому развертка поверхности шара может быть выполнена только приближенными способами. Рассмотрим один из способов выполнения развертки шара.

Для выполнения развертки поверхности шара поверхность делят меридианами на равные части. На рис. 5.35, а шар разделен на 12 равных частей. Представим себе, что все 12 частей поверхности шара ото­гнуты от полюсов и поставлены в вертикальное положение. Сферическая поверхность условно развернется как цилиндрическая поверхность, состоящая из 12 вертикально расположенных секций. Если эти секции разместить в одной плоскости, то получится приближенная развертка поверхности шара, рис. 5.35, б. Для построения 12 меридианов очерковые окружности шара на горизонтальной и фронтальной проекциях делят на 12 равных частей.

На горизонтальной проекции меридианы спроецируются в отрезки, проходящие через центр проекции шара. Фронтальные проекции этих меридианов будут кривыми, и их строят с помощью параллелей, прове­денных через точки деления фронтального меридиана.

Для построения развертки достаточно знать размеры одной секции. На рис. 5.35, а выделена одна такая секция, на проекциях которой отмечены точки пересечения двух меридианов, являющихся ее сторонами, с параллелями. Так как экватор делит секцию на две одинаковые части (верхнюю и нижнюю). То точки взяты только на той части секции, которая расположена выше экватора.

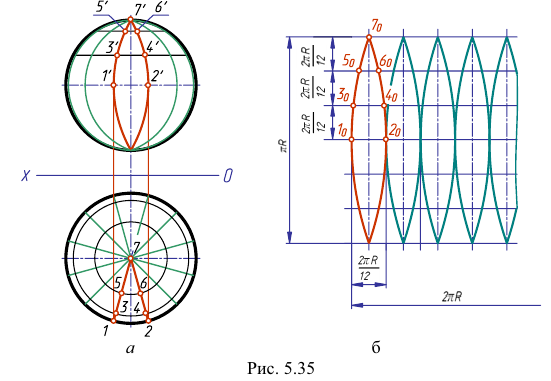
Самый широкий участок секции расположен по экватору. Его ширина равна 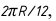то есть 1/12 части экватора. Длина выпрямленной секции равна 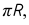то есть длине половины развернутого меридиана.

При развертке поверхности шара экватор развернется в отрезок, длина которого будет равна 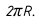Построение начинают с проведения прямой, на которой откладывают 12 отрезков, равных 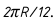На рис. 5.35, б показано построение только части развертки поверхности шара, так как все секции одинаковы.

Через середину построенных отрезков проводят оси симметрий перпендикулярно экватору. Затем вверх и вниз от экватора откладывают длину развернутых участков меридианов, заключенных между параллелями. Их длина равна 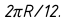Через полученные точки параллельно эк­ватору проводят прямые линии, на которых откладывают отрезки развернутых параллелей 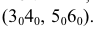Эти отрезки равны 1/12 длины окружности, в которую проецируется соответствующая параллель на горизонтальной проекции. Построенные точки соединяют плавной кривой ли­нией и обводят по лекалу. Эту же развертку можно выполнить, заменяя развернутые дуги хордами, измеренными на ортогональных проекциях.