
Резонанс токов
Содержание:
Резонанс токов:
При рассмотрении параллельного соединения катушки и конденсатора был отмечен случай равенства активной и реактивной проводимостей 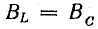
Условия возникновения резонанса
Так же как и резонанс напряжений, резонанс токов возникает, когда частота источника энергии равна резонансной частоте ωр, а 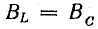
Режим электрической цепи при параллельном соединении участков с индуктивностью и емкостью, характеризующийся равенством индуктивной и емкостной проводимостей, называют резонансом токов.
Сначала рассмотрим этот режим для схемы идеализированной цепи (рис. 17.6, а). В этой схеме параллельно резистору R включены идеальные катушки L и конденсатор С, потери энергии в которых не учитываются.
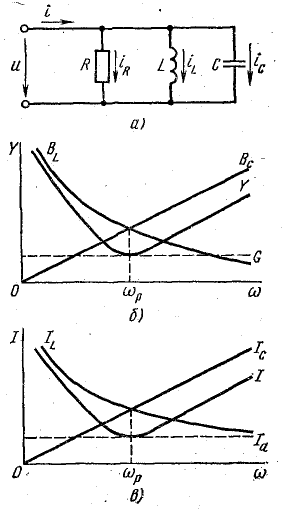
Рис. 17.6. К вопросу о резонансе токов
Реактивные проводимости зависят от частоты вынужденных колебаний. Для рассматриваемой схемы:
активная проводимость
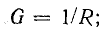
реактивные проводимости
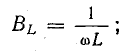
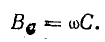
При резонансе токов
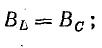
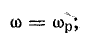
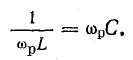
Отсюда определяют резонансную частоту:
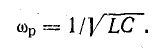
Выражение для резонансной частоты в данном случае такое же, какое было получено при рассмотрении резонанса напряжений [см. формулу (17.8)] и для частоты собственных колебаний в контуре без потерь.
Резонанс токов, так же как и резонанс напряжений, можно получить изменением параметров L и С или изменением частоты источника энергии.
Резонансные кривые
На рис. 17.6, б показаны зависимости проводимостей от частоты. Полная проводимость цепи Y при резонансной частоте ωр оказывается наименьшей, равной активной проводимости G. При изменении частоты в обе стороны от резонансной полная проводимость увеличивается.
При заданном напряжении источника энергии ток в цепи пропорционален проводимости (рис. 17.6, в): 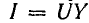 , поэтому кривая I(ω) по форме повторяет кривую Y(ω). Состояние резонанса токов характеризуется наименьшей величиной тока в цепи и равенством нулю угла сдвига фаз между напряжением и током (φр = 0).
, поэтому кривая I(ω) по форме повторяет кривую Y(ω). Состояние резонанса токов характеризуется наименьшей величиной тока в цепи и равенством нулю угла сдвига фаз между напряжением и током (φр = 0).
При резонансе токов отношение тока индуктивного или емкостного к току в неразветвленной части цепи равно отношению волновой проводимости 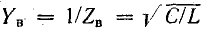 к активной проводимости цепи G.
к активной проводимости цепи G.
Реактивные проводимости при резонансе
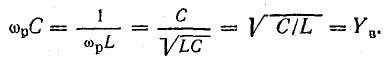
Поэтому
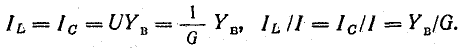
Добротность контура
При параллельном соединении элементов качество резонансной цепи считается тем выше, чем больше отношение 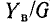 , которое и в этом случае называется добротностью:
, которое и в этом случае называется добротностью:
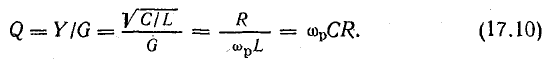
Чем меньше потери энергии в цепи (этому соответствует большая величина R), тем больше добротность.
Параметры реальных катушек и конденсаторов (R, L, С) измеряются и задаются в справочниках применительно к их схемам замещения с последовательным соединением активных и реактивных элементов (см. рис. 14.11, б).
Условие резонанса токов — равенство реактивных проводимостей обеих ветвей 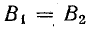 — остается справедливым, и в этом случае
— остается справедливым, и в этом случае
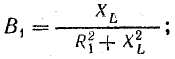
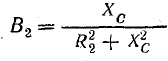 ,
,
где R1 и R2 — активные сопротивления катушки и конденсатора с потерями.
Приравнивая реактивные проводимости, получим исходное уравнение для определения резонансной частоты
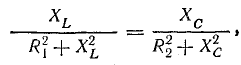
или
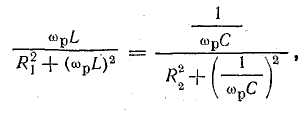
откуда
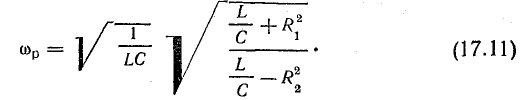
Из «того выражения видно, что резонансная частота зависит от активных сопротивлений катушки и конденсатора. Если потери энергии в катушке и конденсаторе малы (R1 и R2 малы) и ими можно пренебречь, для резонансной частоты получается выражение, найденное раньше для идеализированной цепи.
Компенсация реактивной мощности в электрических сетях с помощью конденсаторов
Было отмечено, что в электрической цепи переменного тока, в которой имеются катушка индуктивности и конденсатор, включенные последовательно или параллельно, общая реактивная мощность цепи всегда меньше, чем реактивная мощность каждого из элементов.
Благодаря взаимному обмену энергией между катушкой и конденсатором и рис. 14.5 источник частично или полностью освобождается от поставки реактивной энергии в цепь.
В этом случае говорят о компенсации реактивной мощности катушки реактивной мощностью конденсатора и наоборот (реактивные мощности QL и QС имеют противоположные знаки). Полная компенсация реактивной мощности имеет место при резонансе.
Компенсация реактивной мощности в электрических сетях имеет большое технико-экономическое значение. Далее кратко рассмотрены общие сведения по этому вопросу и принцип применения конденсаторов для компенсации реактивной мощности.
Реактивная мощность электрических установок
Энергетический процесс в катушке индуктивности, включенной в цепь переменного тока, характеризуется активной мощностью 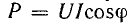 и реактивной мощностью
и реактивной мощностью 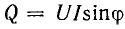 .
.
В электрической схеме замещения такая катушка представлена активным сопротивлением R и индуктивностью L, или активной проводимостью G и реактивной проводимостью Y.
В этом отношении катушке индуктивности подобны многочисленные устройства переменного тока: асинхронные двигатели, индукционные нагревательные установки, трансформаторы, воздушные линии и др.
Получая от генераторов электрическую энергию, эти устройства передают или преобразуют ее в другие виды энергии (активная мощность Р), т. е. выполняют те функции, для которых созданы.
Одновременно они обмениваются энергией с источниками (реактивная мощность Q), что является процессом хотя и нежелательным, но неизбежным, так как без магнитного поля и периодического накопления энергии в нем перечисленные устройства работать не могут.
Если реактивная мощность устройства не равна нулю, то отношение 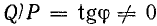 , а коэффициент мощности
, а коэффициент мощности 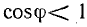 .
.
На каждом предприятии одновременно работают электродвигатели (их может быть десятки и сотни), трансформаторы и другие устройства. Чем больше их число и чем меньше их коэффициент мощности, тем больше общая реактивная мощность электрооборудования производственного участка, цеха, всего предприятия.
Величина общей реактивной мощности электрической установки или электрооборудования предприятия в целом зависит еще и от правильного выбора, степени загрузки электродвигателей, трансформаторов, от соблюдения правил эксплуатации электрооборудования.
Далее будет показано, что за счет реактивной мощности потребителей электрический ток в сетях оказывается больше, чем требуется по величине активной нагрузки. С этим связана одна из проблем проектирования и эксплуатации электрических сетей. При передаче электрической энергии, особенно на большие расстояния, из-за наличия индуктивных и емкостных сопротивлений в элементах сети переменного тока возникает также проблема поддержания заданного уровня напряжения на всех приемниках.
Для обеспечения оптимальной величины тока и требуемых величин напряжения в сети необходимо иметь оптимальный баланс реактивных мощностей (индуктивной и емкостной).
Влияние величины реактивной мощности на технико-экономические показатели электроустановок
Для выяснения влияния величины реактивной мощности на экономические показатели электротехнических установок рассмотрим приемник энергии (например, асинхронный электродвигатель), работающий с постоянной активной мощностью при постоянном напряжении в сети.
Ток в приемнике, а следовательно, и в проводах, соединяющих его с источником энергии, при этих условиях зависит от величины реактивной мощности Q:
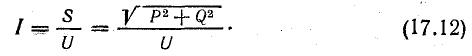
Чем больше реактивная мощность приемника, тем больший ток должен быть в самом приемнике, в генераторе, соединительных проводах, трансформаторе и других элементах сети электроснабжения.
Мощность тепловых потерь, согласно закону Ленца — Джоуля, пропорциональна квадрату тока и сопротивлению проводов:
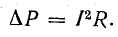
Очевидно, чем больше ток приемника, тем больше потери энергии во всех элементах электрической цепи.
Стоимость потерянной энергии входит в эксплуатационные расходы. Уменьшение реактивной мощности приемников ведет к уменьшению их токов, сокращению потерь энергии и эксплуатационных расходов.
Если электрическая установка спроектирована с относительно большей величиной реактивной мощности, то оборудование (коммутационная аппаратура, приборы контроля и т. д.) и провода необходимо выбрать на большие токи, чем при меньшей величине реактивной мощности.
Это значит, что оборудование должно быть установлено относительно больших размеров, а провода — большего сечения. Последнее повлечет за собой увеличение объема зданий, утяжеление фундаментов и опор и т. п.
Уменьшение реактивной мощности приемников энергии сокращает капитальные затраты.
Генераторы электрической энергии и трансформаторы характеризуются номинальной мощностью — произведением номинальных величин напряжения и тока: 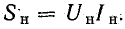
Наиболее полное использование генераторов и трансформаторов соответствует режиму работы с номинальным током при номинальном напряжении (особые случаи, когда допускается некоторая перегрузка оборудования при эксплуатации, здесь не учитываются).
Величина активной мощности генератора равна активной мощности питающихся от него приемников.
Если реактивная мощность приемников равна нулю, то генератор может развивать активную мощность, равную его номинальной мощности , т. е. основная функция генератора — преобразование энергии — может быть выполнена наиболее полно, а первичный двигатель (например, турбина), также рассчитанный на номинальную мощность, будет работать с полной нагрузкой.
При наличии у приемников реактивной мощности активная мощность генератора меньше номинальной, хотя он работает при номинальных напряжении и токе. Таким образом, генератор и первичный двигатель по мощности недогружены, что приводит к снижению их коэффициента полезного действия.
Компенсация реактивной мощности
Из приведенных рассуждений следует, что реактивную мощность установок, потребляющих электрическую энергию, надо по возможности сокращать.
На практике это достигается путем правильного выбора мощности электродвигателей переменного токаи трансформаторов, рациональной эксплуатации их без недогрузки и работы вхолостую. Эти и некоторые другие меры уменьшения реактивной мощности, связанные с выбором и эксплуатацией электрооборудования, называют естественными.
В тех случаях, когда естественные меры не могут обеспечить оптимальной величины реактивной мощности установки, принимают искусственные меры для ее компенсации.
Одной из таких мер является включение параллельно к приемникам батареи конденсаторов.
Для определения мощности и емкости батареи конденсаторов должны быть известны величины напряжения сети U, реактивной мощности установки до компенсации (Q1) и после компенсации (Q2).
Можно установить батарею конденсаторов мощностью QC = Q1, тогда Q2 = 0. Полная компенсация реактивной мощности освобождает полностью сеть от реактивного тока.
Однако технико-экономические расчеты показывают, что полная компенсация в большинстве случаев не является оптимальным решением вопроса, так как компенсационное устройство оказывается более сложным и дорогим, чем при некоторой оптимальной величине реактивной мощности Q2, которую определяют на основе технико-экономического сопоставления вариантов (Определение оптимальной величины Q2, выбор вида компенсирующего устройства и места его установки в сети рассматриваются в специальных курсах).
Мощность батареи конденсаторов
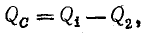
а емкость

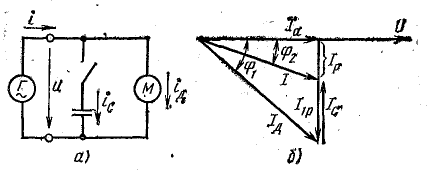
Рис. 17.7. К вопросу о компенсации реактивной мощности
Сущность компенсации реактивной мощности с помощью конденсаторов видна из векторной диаграммы (рис. 17.7, б), построенной для схемы (рис. 17.7, а), на которой параллельно приемнику, например асинхронному двигателю (группе двигателей), может быть включена конденсаторная батарея. До включения конденсаторов ток в подводящих проводах Iд отстает по фазе от напряжения на угол φ1. После включения батареи реактивная составляющая I1р тока двигателя частично компенсируется емкостным током IC, в связи с чем ток в подводящих проводах уменьшается до I, а угол сдвига фаз — до φ2 (в обменном энергетическом процессе между генератором и приемником участвует меньшее количество электромагнитной энергии).
Активная составляющая тока в проводах не изменяется, следовательно, по активной мощности режим цепи остается прежним:
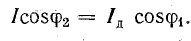
Ток батареи конденсаторов имеет величину
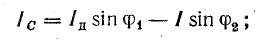
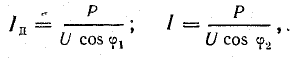
где Р — активная мощность приемника (в данном случае двигателя);
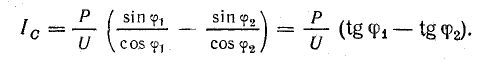
Емкость батареи конденсаторов
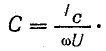
Мощность батареи конденсаторов
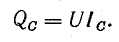
Нетрудно заметить, что мощность конденсаторов можно найти, не подсчитывая тока IC:
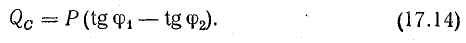
Задача 17.7.
К трансформатору номинальной мощностью 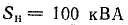 и номинальным напряжением 220 В подключена группа электродвигателей, общая активная мощность которых
и номинальным напряжением 220 В подключена группа электродвигателей, общая активная мощность которых 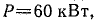
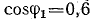 при частоте
при частоте 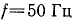 (рис. 17.8, а). Если параллельно группе двигателей включить батарею конденсаторов, реактивная мощность установки (двигатели — батарея конденсаторов) уменьшится и соответственно уменьшится нагрузка трансформатора.
(рис. 17.8, а). Если параллельно группе двигателей включить батарею конденсаторов, реактивная мощность установки (двигатели — батарея конденсаторов) уменьшится и соответственно уменьшится нагрузка трансформатора.
Определить емкость и мощность батареи конденсаторов и дополнительную осветительную нагрузку, которые нужно подключить к трансформатору так, чтобы реактивная мощность установки уменьшилась до величины, при которой коэффициент мощности 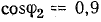 при полной загрузке трансформатора.
при полной загрузке трансформатора.
Определить емкость и мощность батареи конденсаторов в том случае, когда 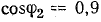 при отсутствии дополнительной осветительной нагрузки.
при отсутствии дополнительной осветительной нагрузки.
Решение. 1. В первоначальном режиме трансформатор был загружен до номинальной мощности
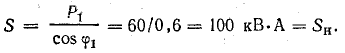
Дополнительную осветительную нагрузку можно присоединить только за счет разгрузки трансформатора от части реактивной мощности путем включения батареи конденсаторов.
Согласно условию задачи, трансформатор после компенсации части реактивной мощности остается полностью загруженным, следовательно, при неизменном напряжении ток трансформатора должен остаться прежним: 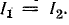
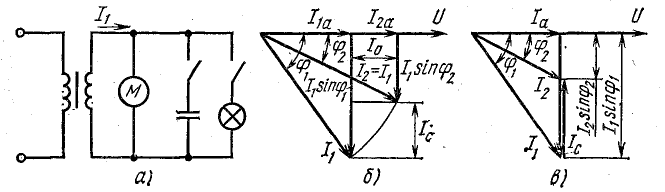
Рис. 17.8. К задаче 17.7
Из векторной диаграммы (рис. 17.8, б) следует выражение для тока конденсатора:
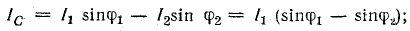
при 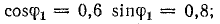
при 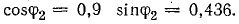
Ток установки до компенсации реактивной мощности
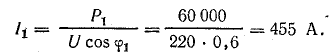
Ток батареи конденсаторов
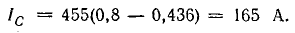
Емкость батареи конденсаторов
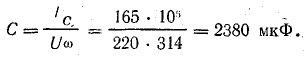
Мощность батареи конденсаторов
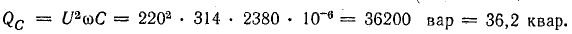
Активный ток дополнительной осветительной нагрузки
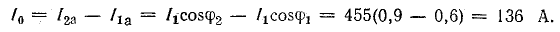
Мощность осветительной нагрузки
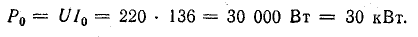
2. При отсутствии дополнительной осветительной нагрузки необходимый ток в батарее конденсаторов (рис. 17.8, в)
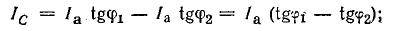
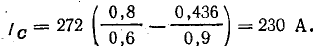
Емкость батареи конденсаторов
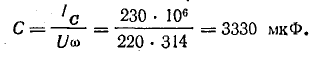
Мощность батареи конденсаторов
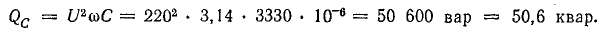
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Трехфазные симметричные цепи
- Трехфазные несимметричные цепи
- Вращающееся магнитное поле
- Электрические цепи синусоидального тока
- Соединение звездой и треугольником в трехфазных цепях
- Принцип действия асинхронного и синхронного двигателей
- Метод симметричных составляющих
- Цепи периодического несинусоидального тока