Резистивные электрические цепи

Содержание:

Расчёт резистивных электрических цепей в статическом режиме:

Приступая к изучению методов анализа электрических цепей, следует напомнить {см. разд. 2.3), что задача анализа включает в себя, во-первых, составление уравнений электромагнитного состояния цепи и, во-вторых, решение этих уравнений относительно искомых величин. Если уравнения найдены, то они могут быть решены какими-либо известными из математики способами. Поэтому изучение методов составления уравнений состояния является важнейшей целью теории цепей.

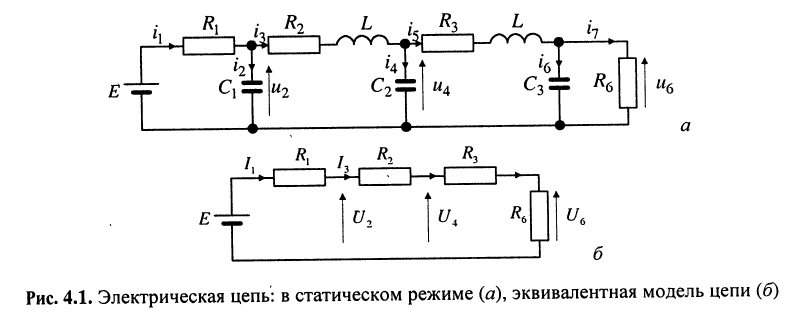
Электрическая цепь характеризуется режимом работы, который определяет характер действующих в ней напряжений и токов. Наиболее просто задача составления уравнений решается для цепей, находящихся в статическом режиме. Говорят, что цепь находится в статическом режиме, если все действующие в ней токи и напряжения являются постоянными. Статический режим соответствует постоянному току (рис. 4.1, а). В этом случае схема замещения индуктивности представляет собой короткозамкнутую цепь, а схема замещения ёмкости — разрыв цепи {см. разд. 3.1.1). Поэтому в эквивалентной модели цепи (рис. 4.1, б), находящейся в статическом режиме, содержатся только резистивные элементы.

Иначе говоря, в статическом режиме имеем резистивную модель цепи, что позволяет ограничиться анализом только резистивной цепи. Тем не менее, результаты, полученные для этого случая, в последующем будут распространены на анализ линейных цепей общего вида.

Расчёт последовательных электрических цепей (делители напряжений)

Рассмотрим последовательную электрическую цепь, состоящую из п рези-стивных элементов и одного источника напряжения
(рис. 4.2).

Задача 4.1.

Определить ток

Решение. Согласно закону Ома для выбранных направлений отсчётов тока и напряжений получим:

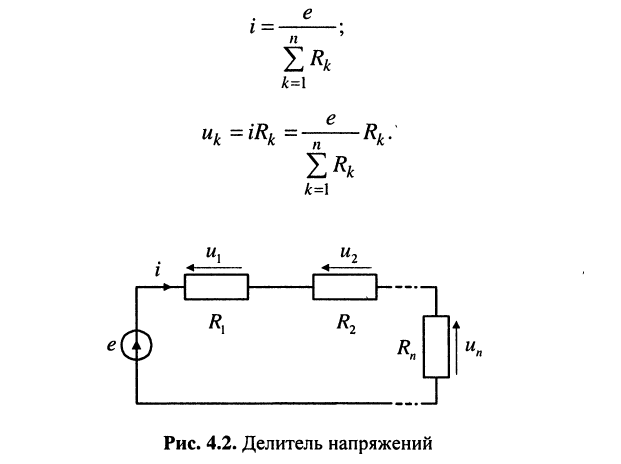
Вывод: для определения напряжения на любом элементе последовательной цепи необходимо заданное напряжение источника разделить на сумму сопротивлении всех резистивных элементов и умножить на сопротивление данного элемента.

Полученное положение часто называют правилом деления напряжений, а саму цепь — делителем напряжений.
 

Расчёт параллельных электрических цепей (делители токов)

Рассмотрим параллельную электрическую цепь, состоящую из 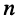резистивных элементов и одного источника тока (рис. 4.3).

Задача 4.2.

Определить напряжение и на зажимах цепи и токи 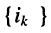в резистивных элементах.

Решение. Согласно закону Ома для выбранных направлений отсчёта тока и напряжений получим:

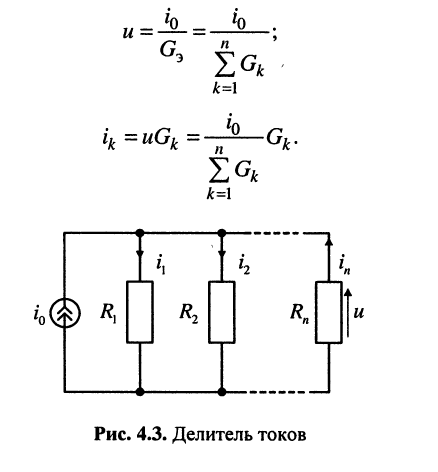
Вывод: для определения тока в любом резистивном элементе параллельной цепи необходимо задающий ток i0 источника разделить на сумму проводимостей всех элементов и умножить на проводимость того элемента, по которому протекает искомый ток.

Полученное положение часто называют правилом деления токов, а саму цепь — делителем токов.

Расчёт параллельно-последовательных электрических цепей

Определение:

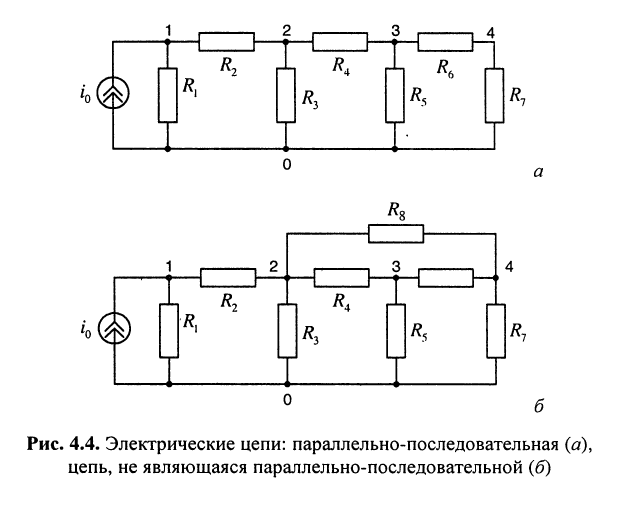
Параллельно-последовательной электрической цепью называется цепь, которая представляет собой совокупность ветвей, связанных между собой только параллельно или последовательно.

Пример такой цепи приведён на рис. 4.4, а, где резистивные элементы 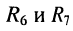включены последовательно; параллельно к ним подключён элемент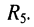. Последовательно с двухполюсником из элементов 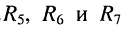подключён элемент 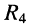и т. д. вплоть до элемента 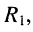соединённого параллельно с источником тока и двухполюсником, образуемым всеми остальными элементами цепи.

Если цепь рис. 4.4, а дополнить резистивным элементом или каким-либо источником, включённым не между смежными узлами, то полученная цепь уже не будет параллельно-последовательной; такая цепь получается, например, при включении элемента 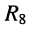между узлами 2 и 4 (рис. 4.4, б).

Расчёт параллельно-последовательных электрических цепей с одним источником

Напряжения и токи в параллельно-последовательных резистивных цепях с одним источником находятся путём эквивалентных преобразований схемы заданной цепи в направлении к источнику тока или источнику напряжения по следующему правилу:

• анализируется структура цепи и выделяется самый удалённый от источника воздействия элемент, от которого и начинаются  эквивалентные преобразования;
• резистивные элементы, соединённые только последовательно или только параллельно, заменяются их эквивалентами;
• эквивалентные замены проводятся до тех пор, пока схема заданной цепи не преобразуется в схему последовательной или  параллельной цепи;
• для полученной эквивалентной цепи по закону Ома находится ток, протекающий через источник напряжения, или напряжение  на зажимах источника задающего тока;
• исходная схема цепи восстанавливается в обратном порядке и на основании правил, установленных в разд. 4.1 и 4.2, находятся   токи, протекающие в элементах, и напряжения на этих элементах.

Пример 4.1.

Найти напряжения на элементах параллельно-последовательной цепи, изображённой на рис. 4.5, а.

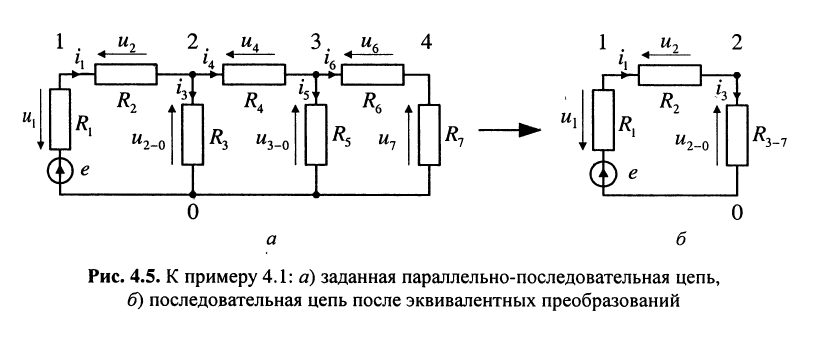
Решение.

Эквивалентные преобразования:

а)    последовательно соединённые элементы 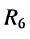и 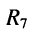, заменяются двухполюсником

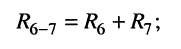
б)    параллельно соединённые элемент 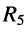и двухполюсник 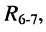включённые между узлами 3 - 0, заменяются двухполюсником

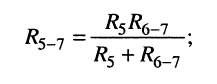
в)    последовательно соединённые элемент 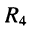и двухполюсник 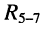заменяются двухполюсником

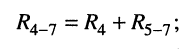
г)    параллельно соединённые элемент 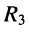и двухполюсник  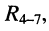включённые между узлами 2 - 0, заменяются двухполюсником

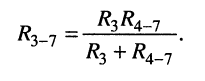
На этом эквивалентные преобразования завершаются, поскольку полученная эквивалентная цепь (рис. 4.5, б) представляет собой последовательное соединение источника напряжения 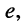элементов 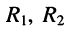и двухполюсника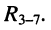

Вычисление токов и напряжений на элементах схемы эквивалентной цепи:

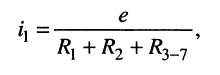
по правилу деления напряжений получаем:

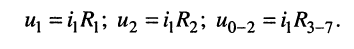
Вычисление токов и напряжений на резистивных элементах схемы исходной цепи (в обратном порядке для восстановления цепи):

а) по правилу деления токов находим ток 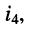протекающий через элемент 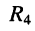и двухполюсник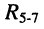  

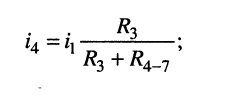
б)    по правилу деления напряжений вычисляем напряжение на элементе 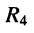и на двухполюснике 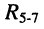(между узлами 3-0)

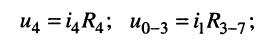
в)    аналогично определяем токи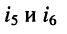

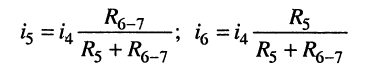
и напряжения на элементах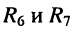

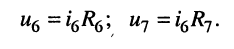
Расчёт параллельно-последовательных электрических цепей с несколькими источниками

Для нахождения токов и напряжений в цепи с несколькими независимыми источниками применяется свойство аддитивности линейной цепи (1.2), называемое часто принципом наложения или суперпозиции, который обычно формулируют в виде теоремы:

Реакция линейной электрической цепи на совокупность воздействий равна сумме реакций, вызываемых в той же цепи каждым из воздействий в отдельности.

Смысл принципа наложения состоит в том, что если к линейной электрической цепи подведено 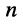 воздействий, например, в виде ЭДС  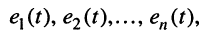то реакция в любом из элементов цепи, например ток 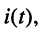будет представлять сумму токов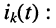

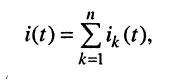
где 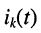— ток в рассматриваемом элементе цепи, вызываемый воздействием ЭДС 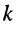-го источника 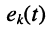при условии, что ЭДС остальных источников положены равными нулю.

Принцип наложения является следствием линейности оператора, с помощью которого описывается электрическая цепь
(см. разд. 1.4). Именно этот принцип может быть использован для практического определения линейности цепи: если в результате эксперимента над некоторой электрической цепью окажется, что реакция цепи на сумму воздействий равна сумме реакций на каждое из воздействий в отдельности, то исследуемая цепь является линейной.

Пример 4.2.

Найти напряжения на резистивном элементе параллельно-последовательной цепи с двумя независимыми источниками, изображённой на рис. 4.6, а.

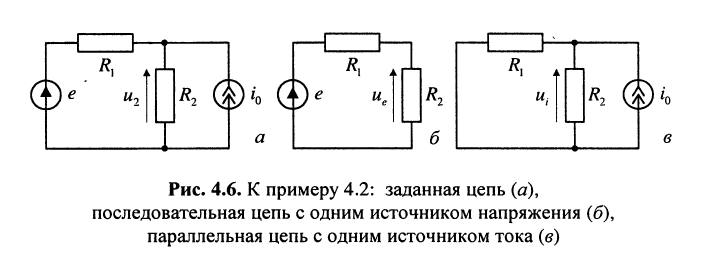
Решение. Согласно принципу наложения напряжение равно сумме напряжений и 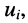создаваемых соответственно источником напряжения и источником тока в отдельности

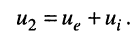
1. Положим, что в цепи имеется только источник напряжения, а задающий ток источника тока равен нулю; в этом случае ветвь, содержащая источник тока, оказывается разомкнутой (рис. 4.6, б); тогда образуется последовательная цепь, в которой

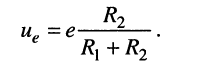    (4.1)

2. Положим, что в цепи имеется только источник тока, а задающее напряжение источника напряжения равно нулю; в этом случае ветвь, содержащая источник напряжения, оказывается замкнутой накоротко (рис. 4.6, в); тогда образуется параллельная цепь, в которой

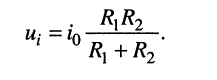(4.2)

Складывая (4.1) и (4.2), окончательно получаем
 

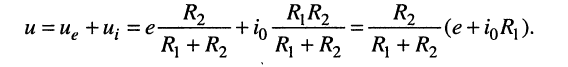  (4.3)

Расчёт электрических цепей методами уравнений Кирхгофа

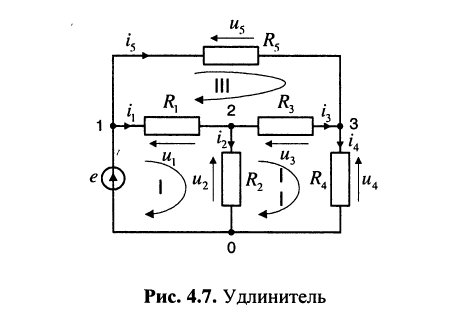
На практике электрические цепи являются не столь простыми, нежели рассмотренные, и далеко не всегда представляют собой комбинацию последовательно и параллельно соединённых ветвей. Примером часто используемой цепи является удлинитель
(рис. 4.7). Расчёт (анализ) таких цепей осуществляются на основании прямого применения законов Кирхгофа (см. лекцию 2).

В зависимости от того, что подлежит определению, различают два метода: метод токов ветвей и метод напряжений ветвей, которые обычно называют прямыми методами расчёта цепей.

Метод уравнений Кирхгофа заключается в составлении и решении трёх групп уравнений:

• уравнений по первому закону Кирхгофа для узлов;
• уравнений по второму закону Кирхгофа для замкнутых контуров;
• уравнений по закону Ома для каждого элемента цепи.

4.4.1. Метод токов ветвей

В методе токов ветвей неизвестными, подлежащими определению, являются токи ветвей. Существо метода состоит в следующем.

Пусть цепь содержит 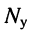узлов и 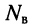ветвей, включая источники напряжения. Поскольку неизвестными являются токи в ветвях, число необходимых независимых уравнений должно быть равно 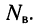По первому закону Кирхгофа можно составить только

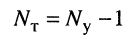
независимых уравнений (2.4).

По второму закону Кирхгофа можно составить только

 

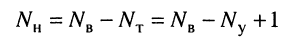
независимых уравнений (2.6).

На основании полученных зависимостей можно сформулировать порядок расчёта цепи рассматриваемым методом:

1. На схеме цепи выбираются положительные направления токов в ветвях и напряжений на элементах.
2. Составляется 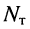независимых уравнений относительно токов в узлах по первому закону Кирхгофа.
3. Составляется 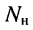независимых уравнений относительно контурных токов по второму закону Кирхгофа.
4. Напряжения на резистивных элементах, входящие в уравнения п. 3, выражаются через токи по закону Ома.
5. Полученная система из 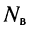уравнений решается относительно искомых величин.

Пример 4.3.

Рассчитать токи всех ветвей удлинителя (см. рис. 4.7).

Решение. Для однозначного составления уравнений выберем направления токов и напряжений такими, как показано на рисунке.

Удлинитель имеет 4 узла и 6 ветвей, поэтому по первому закону Кирхгофа можно составить

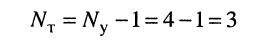
независимых уравнения:

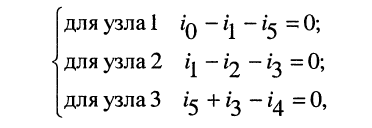 (4.4)

и по второму закону Кирхгофа можно составить также

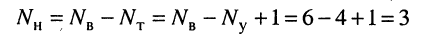
независимых уравнения; при выбранных направлениях обхода контуров получаем:

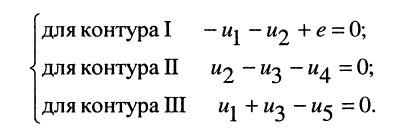   (4.5)

Выразим напряжения , на резисторах через токи 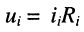; и полученные выражения подставим в систему уравнений для напряжений в контурах:

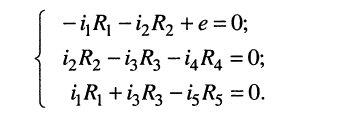   (4.6)

Объединение систем уравнений 4.4 и 4.6 даёт систему (4.7), в которой переменными являются токи ветвей (элементов).

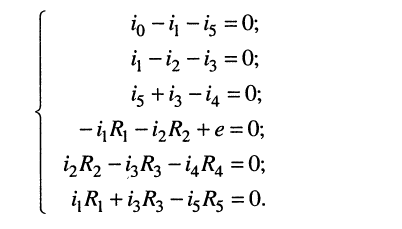  (4.7)

Объединённая система уравнений является неоднородной системой из шести алгебраических уравнений относительно такого же числа неизвестных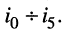

Метод напряжений ветвей

В методе напряжений ветвей неизвестными, подлежащими определению, являются напряжения на элементах цепи. Метод подобен методу, рассмотренному в разд. 4.4.1, а именно: так же, как и в предыдущем случае, составляются две системы уравнений по первому и второму законам Кирхгофа, однако теперь все токи ветвей выражаются через напряжения и проводимости резисторов по закону Ома. Две полученные системы объединяются в одну, результатом решения которой оказываются напряжения на резисторах.

Пример 4.3.

Рассчитать напряжения на элементах удлинителя (см. рис. 4.7) при выбранных на рисунке направлениях токов и напряжений.

Решение. Составляются системы уравнений (4.4) и (4.5), после чего в системе

(4.4)    токи 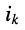выражаются через напряжения 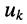на резисторах  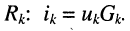В результате получаем систему

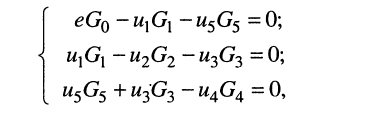   (4.8)

где 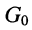является эквивалентной проводимостью всей цепи. Объединением

(4.5)    и (4.8) получаем систему

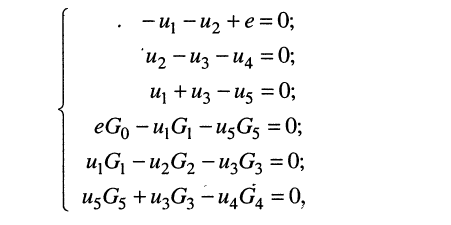    (4.9)

в которой неизвестными являются напряжения на резисторах.

Видно, что метод напряжений ветвей является дуальным по отношению к методу токов ветвей, т. к. для получения системы (4.9) достаточно в системе (4.7) произвести простую замену токов на напряжения и сопротивлений на проводимости.