
Решение уравнений высших степеней с примерами
Содержание:
Решение уравнений высших степеней
Способ разложения на множители
Уравнением 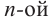
Примеры:
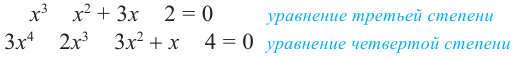
Формулы для нахождения корней уравнений третьей и четвертых степеней известны, однако эти формулы очень сложные. Уравнения высших степеней удобно решать, применяя определенные способы. Один из таких способов разложение на множители
Пример: 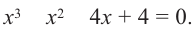 Разложим левую часть на множители, сгруппировав члены как показано ниже:
Разложим левую часть на множители, сгруппировав члены как показано ниже:
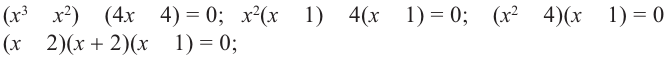
Для того, чтобы произведение было равным нулю, необходимо, чтобы хотя-бы один из множителей был равным нулю. Поэтому 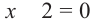 или
или 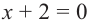 или
или 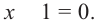 Отсюда
Отсюда 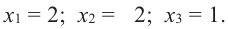
Уравнения, приводимые к квадратным
Ряд уравнений можно привести к квадратным, вводя новую переменную. Например, уравнение 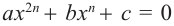 заменой
заменой 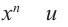 можно привести к уравнению
можно привести к уравнению 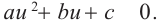 В частном случае, при
В частном случае, при  получается уравнение
получается уравнение 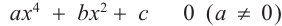 , которое называется биквадратным уравнением и для его решения пользуются заменой
, которое называется биквадратным уравнением и для его решения пользуются заменой 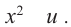 Например:
Например:

Уравнения, содержащие переменную под знаком модуля
При решении уравнений содержащих переменную под знаком модуля рассматриваются два случая.
1-ый случай: выражение, стоящее под знаком модуля положительное или равно нулю.
2-ой случай: выражение, стоящее под знаком модуля отрицательное. По определению 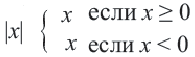
Пример 1. 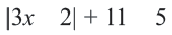
В левой части этого равенства оставим только выражение с модулем: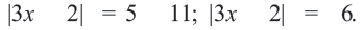 Это противоречит определению модуля, гак как модуль числа должен быть или положительным числом или равным нулю. Решением таких уравнений будет пустое множество. Ответ:
Это противоречит определению модуля, гак как модуль числа должен быть или положительным числом или равным нулю. Решением таких уравнений будет пустое множество. Ответ: 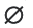
Пример 2. 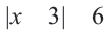
Алгебраический способ решения:
 должен равняться или
должен равняться или 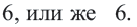
Если 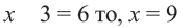
Если 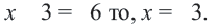
Проверим, удовлетворяют ли данному уравнению найденные значения 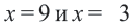 : При
: При 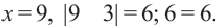 При
При 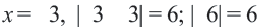
Ответ: Данное уравнение имеет два корня: 9 и 3.
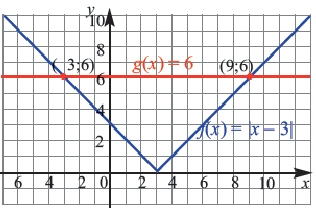
Графический способ решения
В одной и той же координатной плоскости построим графики функций 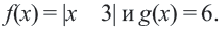 По графику определим точки
По графику определим точки 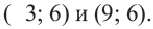 Получаем, что значения
Получаем, что значения 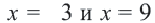 являются корнями уравнения.
являются корнями уравнения.
Пример 3. 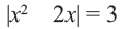
Данное уравнение приводится к совокупности 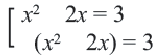
1-ый случай. 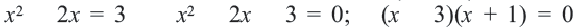
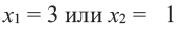
Проверка: 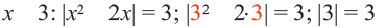 , значит
, значит 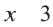 корень уравнения.
корень уравнения.  , значит
, значит 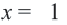 корень уравнения.
корень уравнения.
2-ой случай. 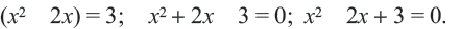 Дискриминант отрицательный. Решений нет.
Дискриминант отрицательный. Решений нет.
Итак, решением данного уравнения будет: 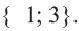
Пример 4. 
По определению абсолютной величины числа: 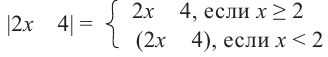
1 случай. Если 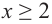 то,
то, 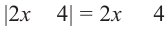 и данное уравнение преобразуется к виду:
и данное уравнение преобразуется к виду:  Это записывается так:
Это записывается так:
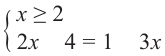
Из уравнения 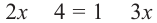 находим
находим 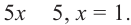 А это значение не удовлетворяет условию
А это значение не удовлетворяет условию 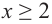 . То есть в этом случае уравнение не имеет корней.
. То есть в этом случае уравнение не имеет корней.
2 случай. Если 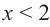 , то
, то 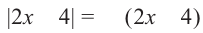 и данное уравнение примет вид:
и данное уравнение примет вид: 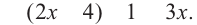 В этом случае получаем систему:
В этом случае получаем систему:
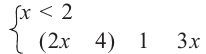
Из уравнения 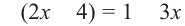 находим
находим  , а это значение удовлетворяет условию
, а это значение удовлетворяет условию 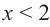 . Таким образом, данное уравнение имеет один корень. Ответ:
. Таким образом, данное уравнение имеет один корень. Ответ: 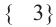 .
.
Пример: 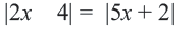
Решение: 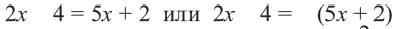
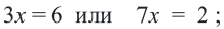
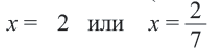
Проверка: 
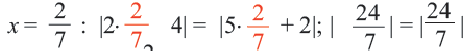
Ответ: 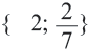
Системы уравнений
Уравнения с двумя переменными. Системы уравнений
Примеры уравнений с двумя переменными
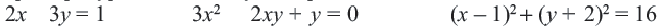
Решением уравнения с двумя переменными называется пара значений переменных 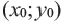 , обращающая уравнение в верное равенство. Например, пара чисел
, обращающая уравнение в верное равенство. Например, пара чисел 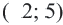 , первое из которых означает значение переменной
, первое из которых означает значение переменной 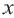 , а второе переменной
, а второе переменной 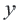 является решением уравнения
является решением уравнения 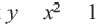 (т.к. верно равенство
(т.к. верно равенство 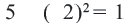 ). Графиком уравнения с двумя переменными является множество точек на координатной плоскости, координаты которых являются решениями уравнения. Например, графиком уравнения
). Графиком уравнения с двумя переменными является множество точек на координатной плоскости, координаты которых являются решениями уравнения. Например, графиком уравнения 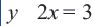 является прямая, графиком уравнения
является прямая, графиком уравнения 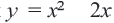 парабола, а графиком уравнения
парабола, а графиком уравнения 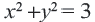 является окружность.
является окружность.
Если ставится задача найти множество общих решений двух или нескольких уравнений с двумя (или более) переменными - значит нужно решить систему. Пару 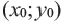 , являющуюся решением каждого уравнения системы, называют решением системы, а совокупность всех пар называют множеством решений системы.
, являющуюся решением каждого уравнения системы, называют решением системы, а совокупность всех пар называют множеством решений системы.
Системы уравнений в которой одно уравнение первой, а другое второй степени
Графический способ. Решение системы можно определить, построив графики обеих уравнений в одной координатной плоскости и найдя координаты точек пересечения (хотя бы приблизительно). Обычно решение системы графическим способом удобно, когда нужно найти количество корней.
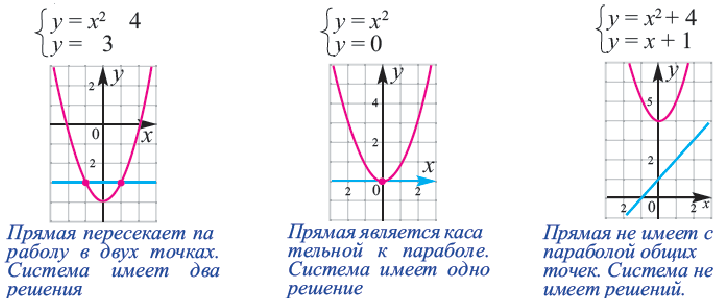
Система уравнений.
Пример 1. 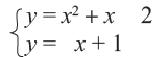
В одной системе координат построим графики, соответствующие каждому уравнению системы. Графиком уравнения 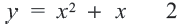 является парабола, а графиком уравнения
является парабола, а графиком уравнения 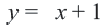 прямая. Определим координаты точек пересечения графиков:
прямая. Определим координаты точек пересечения графиков: 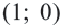 и
и 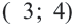 . Подставив эти значения в уравнения системы, можно проверить, что в этом случае решения были найдены точно.
. Подставив эти значения в уравнения системы, можно проверить, что в этом случае решения были найдены точно.
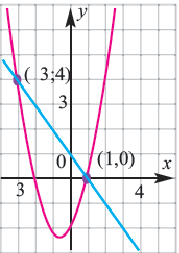


Ответ: 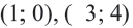
Пример 2.
Определите сколько решений имеет система 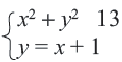
Решение: Построив окружность с заданным уравнением 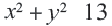 и прямую
и прямую 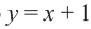 в одной системе координат, можно увидеть что они пересекаются в двух точках. Пара
в одной системе координат, можно увидеть что они пересекаются в двух точках. Пара 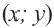 - координаты этих точек являются решениями данной системы уравнения.
- координаты этих точек являются решениями данной системы уравнения.
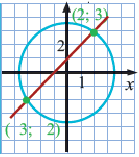
Ответ: Данная система имеет два решения
Решение системы уравнений, в которой одно уравнение первой, а другое второй степени, алгебраическим путем.
Способ подстановки
Способ подстановки:
1) Из уравнения первой степени выражается одна переменная через другую.
2) Полученное выражение подставляется в другое уравнение системы и получается уравнение с одним неизвестным.
3) Решив это уравнение, находится значение неизвестного.
4) По найденному значению одного неизвестного находится другое неизвестное.
Пример: 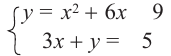
1) Выразим 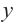 через
через 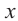 из уравнения
из уравнения 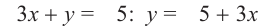
2) Подставим в уравнение  выражение
выражение 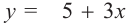 и получим:
и получим:
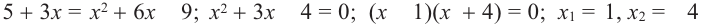
3) Подставим значения 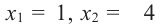 в выражение
в выражение 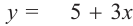 и найдем.
и найдем. 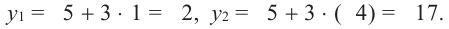
4) Ответ: 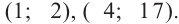
Способ почленного сложения (или вычитания)
Пример 2. 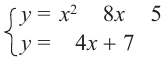 Выполним последовательно решение системы.
Выполним последовательно решение системы.
1) Вычтем из первого уравнения второе, 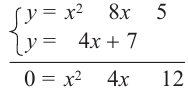
2) Решим полученное уравнение: 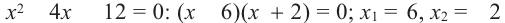
3) Подставим значения 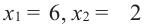 в одно из уравнений системы и получим:
в одно из уравнений системы и получим: 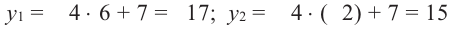
4) Ответ: 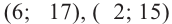
При помощи дискриминанта определите число решений системы.
Пример: 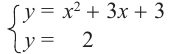
Применив способ почленного вычитания, получим квадратное уравнение 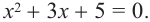 Определим знак дискриминанта:
Определим знак дискриминанта: 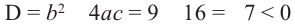 . Так как дискриминант отрицательный, то данная система не имеет решений.
. Так как дискриминант отрицательный, то данная система не имеет решений.
Пример: Прямая с угловым коэффициентом 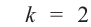 имеет с параболой
имеет с параболой 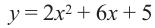 общую точку. Определите ординату точки пересечения прямой с осью
общую точку. Определите ординату точки пересечения прямой с осью 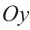 .
.
Решение: Так как 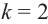 , то уравнением прямой будет
, то уравнением прямой будет 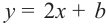 .
.
Из системы уравнений: 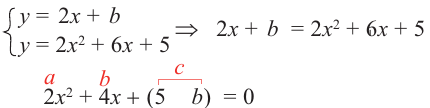
Так как, по условию система имеет одно решение, то дискриминант уравнения равен 0.
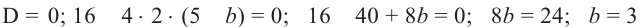
Уравнение прямой будет: 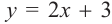 . Значение
. Значение 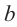 определяет точку пересечения прямой с осью
определяет точку пересечения прямой с осью 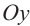 . Другими словами, при
. Другими словами, при 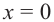 прямая пересекает ось
прямая пересекает ось 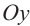 . Если
. Если 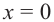 , то
, то 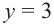 .
.
Ответ: 3
Напишите систему уравнений, соответствующую графику.
Пример: 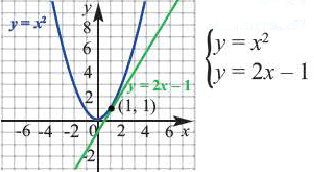
Системы уравнений, в которой оба уравнения второй степени
Количество решений системы уравнений, в которых оба уравнения второй степени можно определить графическим способом 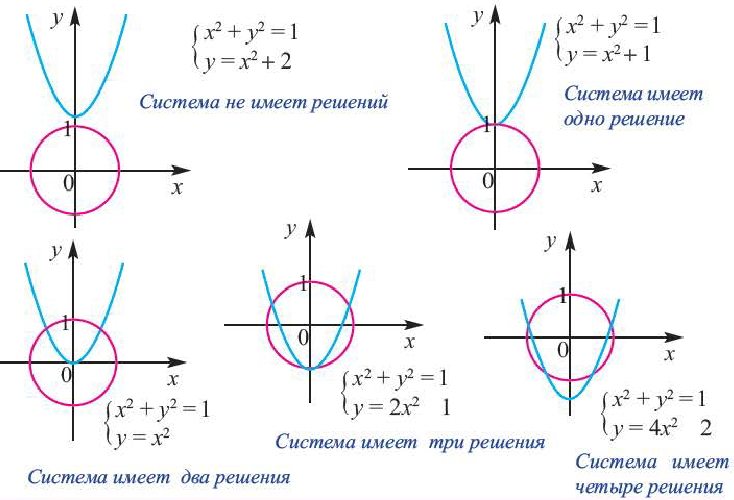
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |