
Решение треугольников - формулы и задачи с примерами решения
Содержание:
В этой лекции вы узнаете, что представляют собой синус, косинус и тангенс угла 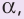
Решение треугольников
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам).
Синус, косинус и тангенс угла от 0 до 180
Понятия синуса, косинуса и тангенса острого угла вам известны из курса геометрии 8 класса. Расширим эти понятия для произвольного угла 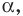 где
где 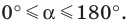
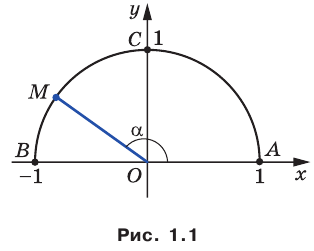
В верхней полуплоскости координатной плоскости рассмотрим полуокружность с центром в начале координат, радиус которой равен 1 (рис. 1.1). Такую полуокружность называют единичной.
Будем говорить, что углу 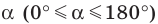 соответствует точка
соответствует точка 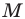 единичной полуокружности, если
единичной полуокружности, если 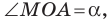 где точки
где точки 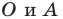 имеют соответственно координаты
имеют соответственно координаты 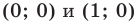 (рис. 1.1). Например, на рисунке 1.1 углу, равному
(рис. 1.1). Например, на рисунке 1.1 углу, равному  соответствует точка
соответствует точка 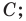 углу, равному
углу, равному 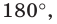 — точка
— точка 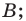 углу, равному
углу, равному 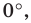 — точка
— точка 
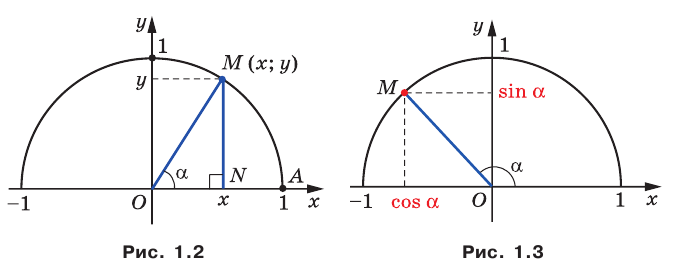
Пусть  — острый угол. Ему соответствует некоторая точка
— острый угол. Ему соответствует некоторая точка  дуги
дуги 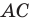 единичной полуокружности (рис. 1.2). В прямоугольном треугольнике
единичной полуокружности (рис. 1.2). В прямоугольном треугольнике 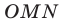 имеем:
имеем:
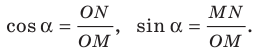
Поскольку 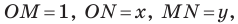 то
то 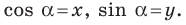
Итак, косинус и синус острого угла 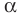 — это соответственно абсцисса и ордината точки
— это соответственно абсцисса и ордината точки 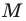 единичной полуокружности, соответствующей углу
единичной полуокружности, соответствующей углу 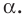
Полученный результат подсказывает, как определить синус и косинус произвольного угла  где
где 
Определение. Косинусом и синусом угла 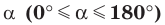 называют соответственно абсциссу и ординату точки
называют соответственно абсциссу и ординату точки 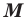 единичной полуокружности, соответствующей углу
единичной полуокружности, соответствующей углу 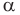 (рис. 1.3).
(рис. 1.3).
Пользуясь этим определением, можно, например, установить, что 
Если 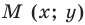 — произвольная точка единичной полуокружности, то
— произвольная точка единичной полуокружности, то  Следовательно, для любого угла
Следовательно, для любого угла 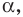 где
где 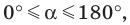 имеем:
имеем:
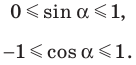
Если 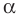 — тупой угол, то абсцисса точки, соответствующей этому углу, отрицательна. Следовательно, косинус тупого угла является отрицательным числом. Справедливо и такое утверждение: если
— тупой угол, то абсцисса точки, соответствующей этому углу, отрицательна. Следовательно, косинус тупого угла является отрицательным числом. Справедливо и такое утверждение: если 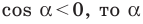 — тупой или развернутый угол.
— тупой или развернутый угол.
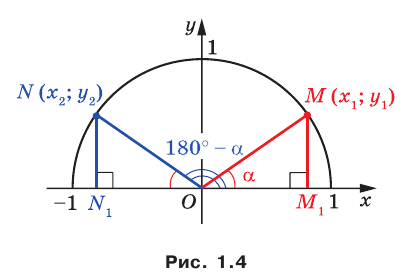
Из курса геометрии 8 класса вы знаете, что для любого острого угла а выполняются равенства: 
Эти формулы остаются справедливыми также для  и для
и для 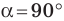 (убедитесь в этом самостоятельно).
(убедитесь в этом самостоятельно).
Пусть углам 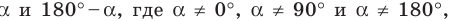 соответствуют точки
соответствуют точки 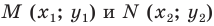 единичной полуокружности (рис. 1.4).
единичной полуокружности (рис. 1.4).
Прямоугольные треугольники 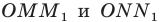 равны по гипотенузе и острому углу
равны по гипотенузе и острому углу 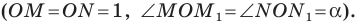 Отсюда
Отсюда 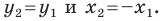 Следовательно,
Следовательно,

Убедитесь самостоятельно, что эти равенства остаются верными для 
Если  — острый угол, то, как вы знаете из курса геометрии 8 класса, справедливо равенство, которое называют основным тригонометрическим тождеством:
— острый угол, то, как вы знаете из курса геометрии 8 класса, справедливо равенство, которое называют основным тригонометрическим тождеством:

Это равенство остается верным для  (убедитесь в этом самостоятельно).
(убедитесь в этом самостоятельно).
Пусть 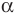 — тупой угол. Тогда угол
— тупой угол. Тогда угол 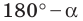 является острым. Имеем:
является острым. Имеем:
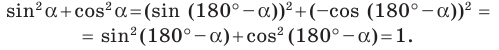
Следовательно, равенство 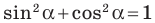 выполняется для всех
выполняется для всех 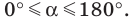
Определение. Тангенсом угла 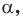 где
где 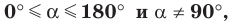 называют отношение
называют отношение 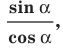 то есть
то есть

Поскольку 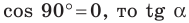 не определен для
не определен для 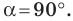
Очевидно, что каждому углу 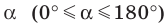 соответствует единственная точка единичной полуокружности. Значит, каждому углу
соответствует единственная точка единичной полуокружности. Значит, каждому углу 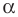 соответствует единственное число, которое является значением синуса (косинуса, тангенса для
соответствует единственное число, которое является значением синуса (косинуса, тангенса для 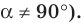 Поэтому зависимость значения синуса (косинуса, тангенса) от величины угла является функциональной.
Поэтому зависимость значения синуса (косинуса, тангенса) от величины угла является функциональной.
Функции 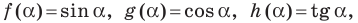 соответствующие этим функциональным зависимостям, называют тригонометрическими функциями угла
соответствующие этим функциональным зависимостям, называют тригонометрическими функциями угла 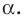
Пример №1
Докажите, что 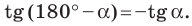
Решение:
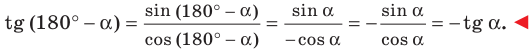
Пример №2
Найдите 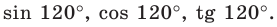
Решение:
Имеем: 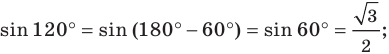
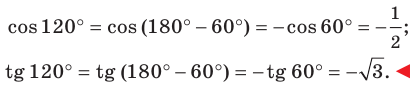
Теорема косинусов
Из первого признака равенства треугольников следует, что две стороны и угол между ними однозначно определяют треугольник. А значит, по указанным элементам можно, например, найти третью сторону треугольника. Как это сделать, показывает следующая теорема.
Теорема 2.1 (теорема косинусов). Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса угла между ними.
Доказательство: Рассмотрим треугольник 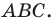 Докажем, например, что
Докажем, например, что
Возможны три случая:
- угол
 острый;
острый; - угол
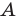 тупой;
тупой; - угол
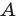 прямой.
прямой.
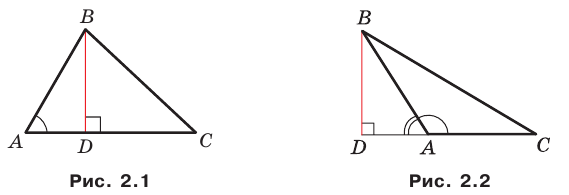
Первый случай. Пусть угол 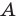 острый. Тогда хотя бы один из углов
острый. Тогда хотя бы один из углов 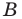 или
или 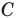 является острым.
является острым.
Пусть 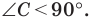 Проведем высоту
Проведем высоту 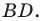 Она будет полностью принадлежать треугольнику
Она будет полностью принадлежать треугольнику 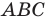 (рис. 2.1). В прямоугольном треугольнике
(рис. 2.1). В прямоугольном треугольнике 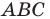 :
:
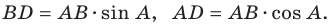
В прямоугольном треугольнике 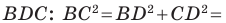
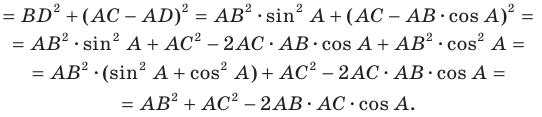
Пусть 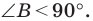 Проведем высоту треугольника
Проведем высоту треугольника 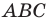 из вершины
из вершины  Она будет полностью принадлежать треугольнику
Она будет полностью принадлежать треугольнику 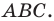 Доказательство для этого случая аналогично рассмотренному. Проведите его самостоятельно.
Доказательство для этого случая аналогично рассмотренному. Проведите его самостоятельно.
Второй случай. Пусть угол 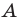 тупой. Проведем высоту
тупой. Проведем высоту 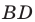 треугольника
треугольника 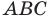 (рис. 2.2).
(рис. 2.2).
В прямоугольном треугольнике 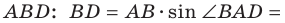
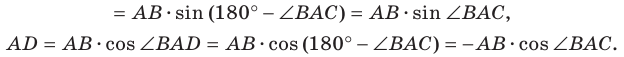
В прямоугольном треугольнике BDC: 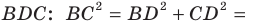
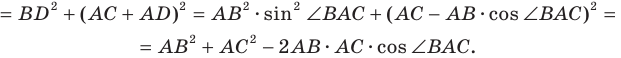
Третий случай. Пусть угол 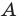 прямой (рис. 2.3). Тогда
прямой (рис. 2.3). Тогда 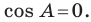 Надо доказать, что
Надо доказать, что 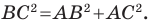 Это равенство следует из теоремы Пифагора для треугольника
Это равенство следует из теоремы Пифагора для треугольника 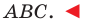
Доказательство теоремы косинусов показывает, что теорема Пифагора является частным случаем теоремы косинусов, а теорема косинусов является обобщением теоремы Пифагора.
Если воспользоваться обозначениями для длин сторон и величин углов треугольника  (см. форзац), то, например, для стороны, длина которой равна
(см. форзац), то, например, для стороны, длина которой равна 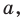 можно записать:
можно записать:
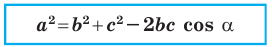
С помощью теоремы косинусов, зная три стороны треугольника, можно определить, является ли он остроугольным, тупоугольным или прямоугольным.
Теорема 2.2 (следствие из теоремы косинусов). Пусть 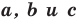 — длины сторон треугольника, причем
— длины сторон треугольника, причем 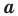 — длина его наибольшей стороны. Если
— длина его наибольшей стороны. Если 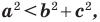 то треугольник является остроугольным. Если
то треугольник является остроугольным. Если 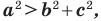 то треугольник является тупоугольным. Если
то треугольник является тупоугольным. Если 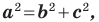 то треугольник является прямоугольным.
то треугольник является прямоугольным.
Доказательство: По теореме косинусов
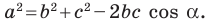
Отсюда 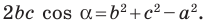
Пусть 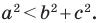 Тогда
Тогда 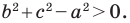 Отсюда
Отсюда  то есть
то есть 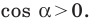 Поэтому угол
Поэтому угол 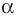 острый.
острый.
Поскольку 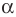 — длина наибольшей стороны треугольника, то против этой стороны лежит наибольший угол, который, как мы доказали, является острым. Следовательно, в этом случае треугольник является остроугольным.
— длина наибольшей стороны треугольника, то против этой стороны лежит наибольший угол, который, как мы доказали, является острым. Следовательно, в этом случае треугольник является остроугольным.
Пусть 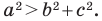 Тогда
Тогда 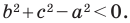 Отсюда
Отсюда  то есть
то есть 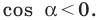 Поэтому угол
Поэтому угол 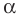 тупой. Следовательно, в этом случае треугольник является тупоугольным.
тупой. Следовательно, в этом случае треугольник является тупоугольным.
Пусть 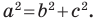 Тогда
Тогда  Отсюда
Отсюда 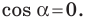 Следовательно,
Следовательно, 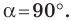 В этом случае треугольник является прямоугольным.
В этом случае треугольник является прямоугольным.
Пример №3
Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Решение:
На рисунке 2.4 изображен параллелограмм  Пусть
Пусть  тогда
тогда 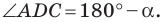 Из треугольника
Из треугольника 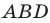 по теореме косинусов получаем:
по теореме косинусов получаем:
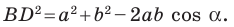
Из треугольника 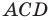 по теореме косинусов получаем:
по теореме косинусов получаем:
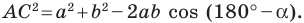 Отсюда
Отсюда
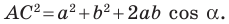
Сложив равенства (1) и (2), получим:
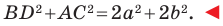
Пример №4
В треугольнике  сторона
сторона 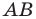 на 4 см больше стороны
на 4 см больше стороны 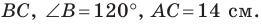 Найдите стороны
Найдите стороны 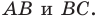
Решение:
По теореме косинусов
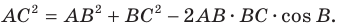
Пусть 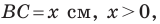 тогда
тогда 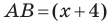 см.
см.
Имеем:
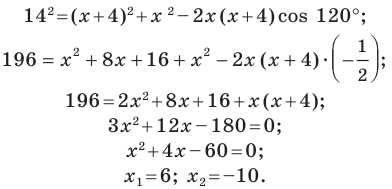
Корень -10 не удовлетворяет условию 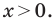
Следовательно, 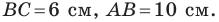
Ответ: 
Пример №5
На стороне  треугольника
треугольника  отметили точку так, что
отметили точку так, что 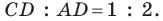 Найдите отрезок
Найдите отрезок 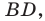 если
если 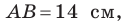
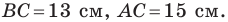
Решение:
По теореме косинусов из треугольника 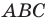 (рис. 2.5) получаем:
(рис. 2.5) получаем:
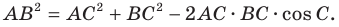
Отсюда 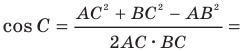
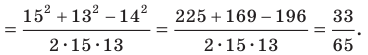
Поскольку 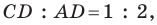 то
то
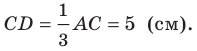
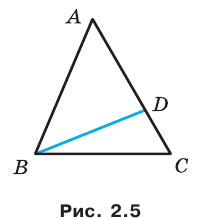
Тогда из треугольника 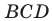 получаем:
получаем:
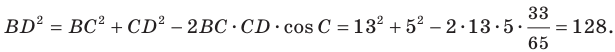
Следовательно, 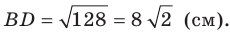
Ответ: 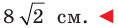
Пример №6
Две стороны треугольника равны 23 см и 30 см, а медиана, проведенная к большей из известных сторон, — 10 см. Найдите третью сторону треугольника.
Решение:
Пусть в треугольнике  известно, что
известно, что 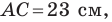
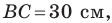 отрезок
отрезок 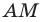 — медиана,
— медиана, 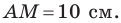
На продолжении отрезка 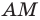 за точку
за точку 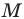 отложим отрезок
отложим отрезок 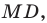 равный медиане
равный медиане 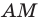 (рис. 2.6). Тогда
(рис. 2.6). Тогда 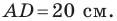
В четырехугольнике  диагонали
диагонали 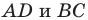 точкой
точкой 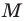 пересечения делятся пополам
пересечения делятся пополам 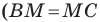 по условию,
по условию, 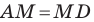 по построению). Следовательно, четырехугольник
по построению). Следовательно, четырехугольник 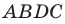 — параллелограмм.
— параллелограмм.
Так как сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон (см. ключевую задачу 1), то 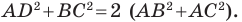
Тогда
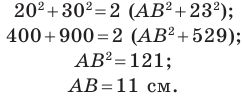
Ответ: 11 см. 
Теорема синусов
При доказательстве ряда теорем и решении многих задач применяют следующую лемму.
Лемма. Хорда окружности равна произведению диаметра и синуса любого вписанного угла, опирающегося на эту хорду.
Доказательство: На рисунке 3.1 отрезок 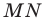 — хорда окружности с центром в точке
— хорда окружности с центром в точке 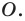 Проведем диаметр
Проведем диаметр 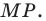 Тогда
Тогда 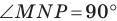 как вписанный угол, опирающийся на диаметр. Пусть величина вписанного угла
как вписанный угол, опирающийся на диаметр. Пусть величина вписанного угла 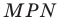 равна
равна 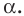 Тогда из прямоугольного треугольника
Тогда из прямоугольного треугольника 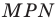 получаем:
получаем:
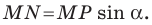
Все вписанные углы, опирающиеся на хорду 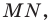 равны
равны 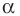 или
или 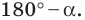 Следовательно, их синусы равны. Поэтому полученное равенство (1) справедливо для всех вписанных углов, опирающихся на хорду
Следовательно, их синусы равны. Поэтому полученное равенство (1) справедливо для всех вписанных углов, опирающихся на хорду 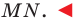
Из второго признака равенства треугольников следует, что сторона
и два прилежащих к ней угла однозначно определяют треугольник. Следовательно, по указанным элементам можно найти две другие стороны треугольника. Как это сделать, подсказывает следующая теорема.
Теорема 3.1 (теорема синусов). Стороны треугольника пропорциональны синусам противолежащих углов.
Доказательство: Пусть в треугольнике 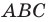 известно, что
известно, что 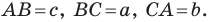 Докажем, что
Докажем, что
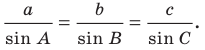
Пусть радиус описанной окружности треугольника 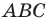 равен
равен 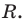 Тогда согласно лемме
Тогда согласно лемме 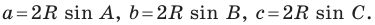 Отсюда
Отсюда
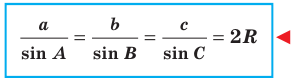
Следствие. Радиус окружности, описанной около треугольника, можно вычислить по формуле
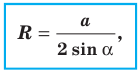
где 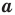 — длина стороны треугольника,
— длина стороны треугольника, 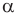 — величина противолежащего этой стороне угла.
— величина противолежащего этой стороне угла.
Пример №7
В треугольнике 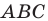 известно, что
известно, что 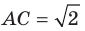 см,
см, 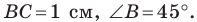 Найдите угол
Найдите угол 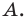
Решение:
По теореме синусов
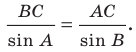
Тогда
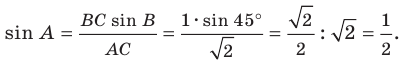
Поскольку 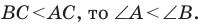 Следовательно, угол
Следовательно, угол 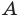 — острый.
— острый.
Отсюда, учитывая, что 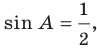 получаем:
получаем: 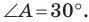
Ответ: 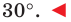
Пример №8
В треугольнике  известно, что
известно, что 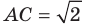
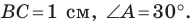 Найдите угол
Найдите угол 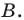
Решение:
По теореме синусов 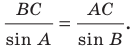 Тогда
Тогда
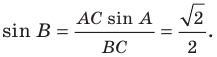
Поскольку 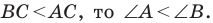 Тогда угол
Тогда угол 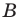 может быть как острым, так и тупым. Отсюда
может быть как острым, так и тупым. Отсюда 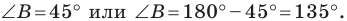
Ответ: 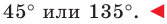
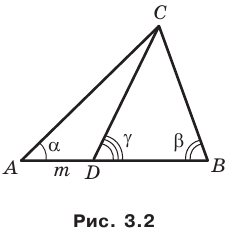
Пример №9
На стороне 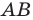 треугольника
треугольника 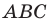 отметили точку
отметили точку 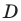 так, что
так, что 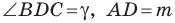 (рис. 3.2). Найдите отрезок
(рис. 3.2). Найдите отрезок 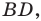 если
если 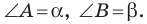
Решение:
Угол 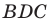 — внешний угол треугольника
— внешний угол треугольника 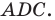 Тогда
Тогда 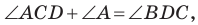 отсюда
отсюда 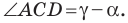
Из треугольника 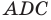 по теореме синусов получаем:
по теореме синусов получаем:
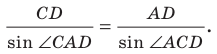
Следовательно,
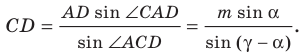 Из треугольника
Из треугольника 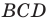 по теореме синусов получаем:
по теореме синусов получаем:
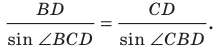
Следовательно,
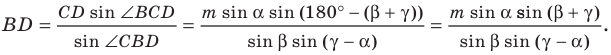
Ответ: 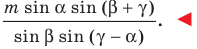
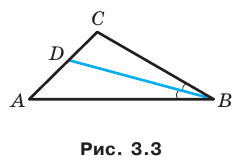
Пример №10
Отрезок 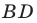 — биссектриса треугольника
— биссектриса треугольника 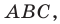
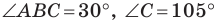 (рис. 3.3). Найдите радиус окружности, описанной около треугольника
(рис. 3.3). Найдите радиус окружности, описанной около треугольника 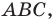 если радиус окружности, описанной около треугольника
если радиус окружности, описанной около треугольника 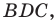 равен
равен 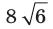 см.
см.
Решение:
Пусть 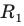 — радиус окружности, описанной около треугольника
— радиус окружности, описанной около треугольника 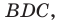
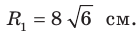
Поскольку отрезок 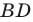 — биссектриса треугольника, то
— биссектриса треугольника, то 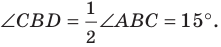
Из треугольника 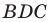 получаем:
получаем: 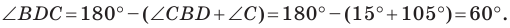
По следствию из теоремы синусов 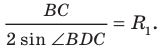 Отсюда
Отсюда
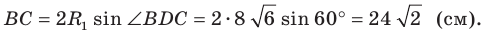
Из треугольника 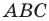 получаем:
получаем:
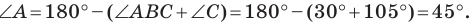
Пусть 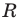 — искомый радиус окружности, описанной около треугольника
— искомый радиус окружности, описанной около треугольника 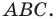
Тогда 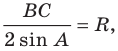 отсюда
отсюда
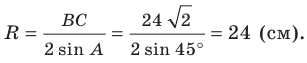
Ответ: 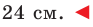
Как решать треугольников
Решить треугольник — это значит найти неизвестные его стороны и углы по известным сторонам и углам
Теоремы косинусов и синусов позволяют решить любой треугольник.
В следующих задачах значения тригонометрических функций будем находить с помощью калькулятора и округлять эти значения до сотых. Величины углов будем находить с помощью калькулятора и округлять эти значения до единиц. Вычисляя длины сторон, результат будем округлять до десятых.
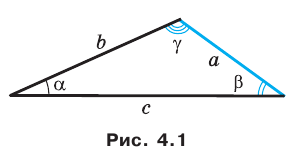
Пример №11
Решите треугольник (рис. 4.1) по стороне 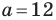 см и двум углам
см и двум углам 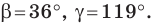
Решение:
Используя теорему о сумме углов треугольника, получаем: 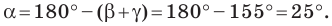
По теореме синусов 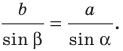
Отсюда 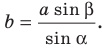
Имеем: 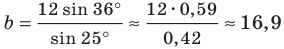
Вновь применяя теорему синусов, запишем:
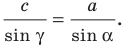
Отсюда 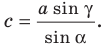
Имеем:
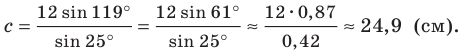
Ответ: 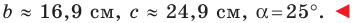
Пример №12
Решите треугольник по двум сторонам 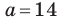 см,
см, 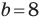 см и углу
см и углу 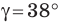 между ними.
между ними.
Решение:
По теореме косинусов 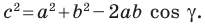
Отсюда
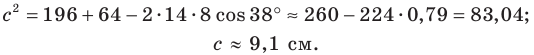
Далее имеем:
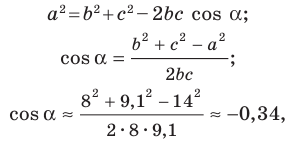
Отсюда 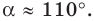
Используя теорему о сумме углов треугольника, получаем:
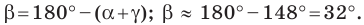
Ответ: 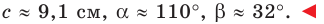
Пример №13
Решите треугольник по трем сторонам 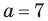 см,
см, 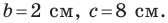
Решение:
По теореме косинусов 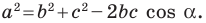 Отсюда
Отсюда
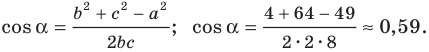 Получаем:
Получаем: 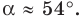
Пo теореме синусов 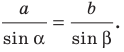 Отсюда
Отсюда
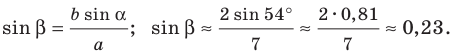
Поскольку 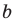 — длина наименьшей стороны данного треугольника, то угол
— длина наименьшей стороны данного треугольника, то угол 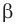 является острым. Тогда находим, что
является острым. Тогда находим, что 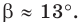 Используя теорему о сумме углов треугольника, получаем:
Используя теорему о сумме углов треугольника, получаем:
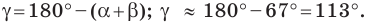
Ответ: 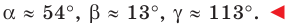
Пример №14
Решите треугольник по двум сторонам и углу, противолежащему одной из сторон:
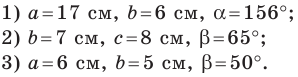
Решение:
1) По теореме синусов 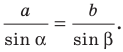
Отсюда 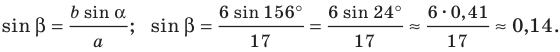
Поскольку угол 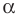 данного треугольника тупой, то угол
данного треугольника тупой, то угол 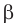 является острым. Тогда находим, что
является острым. Тогда находим, что 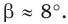
Используя теорему о сумме углов треугольника, получаем:
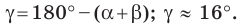
По теореме синусов 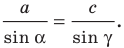
Отсюда 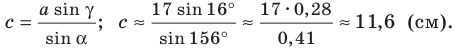
Ответ: 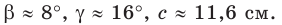
2) По теореме синусов 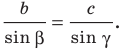
Отсюда 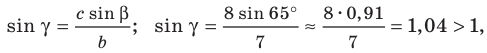 что невозможно.
что невозможно.
Ответ: задача не имеет решения.
3) По теореме синусов 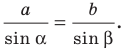 Отсюда
Отсюда
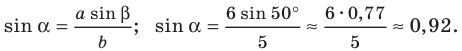
Возможны два случая: 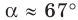 или
или 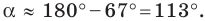
Рассмотрим случай, когда 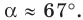
Используя теорему о сумме углов треугольника, получаем:
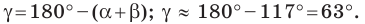
Пo теореме синусов 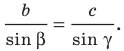
Отсюда 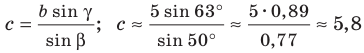 (см).
(см).
Рассмотрим случай, когда 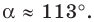
Используя теорему о сумме углов треугольника, получаем:
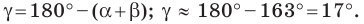
Поскольку 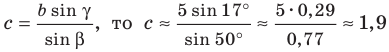 (см)
(см)
Ответ: 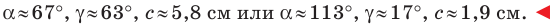
Тригонометрия наука об измерении треугольников
Вы знаете, что древние путешественники ориентировались по звездам и планетам. Они могли достаточно точно определить положение корабля в океане или каравана в пустыне по расположению светил на небосклоне. При этом одним из ориентиров служила высота, на которую поднималось над горизонтом то или иное небесное светило в данной местности в данный момент времени.
Понятно, что непосредственно измерить эту высоту невозможно. Поэтому ученые стали разрабатывать методы косвенных измерений. Здесь существенную роль играло решение треугольника, две вершины которого лежали на поверхности Земли, а третья являлась звездой (рис. 4.3) — знакомая вам задача 3.17. 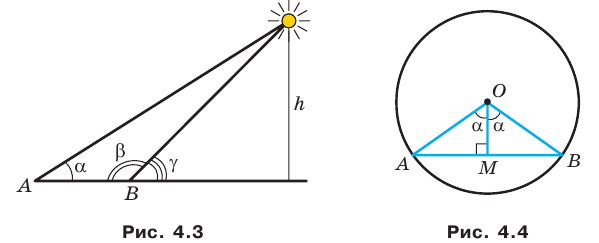
Для решения подобных задач древним астрономам необходимо было научиться находить взаимосвязи между элементами треугольника. Так возникла тригонометрия — наука, изучающая зависимость между сторонами и углами треугольника. Термин «тригонометрия» (от греческих слов «тригонон» — треугольник и «метрео» — измерять) означает «измерение треугольников».
На рисунке 4.4 изображен центральный угол  равный
равный 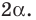 Из прямоугольного треугольника
Из прямоугольного треугольника 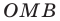 имеем:
имеем: 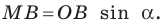 Следовательно, если в единичной окружности измерить половины длин хорд, на которые опираются центральные углы с величинами
Следовательно, если в единичной окружности измерить половины длин хорд, на которые опираются центральные углы с величинами 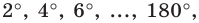 то тем самым мы можем вычислить значения синусов углов
то тем самым мы можем вычислить значения синусов углов 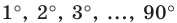 соответственно.
соответственно.
Измеряя длины полухорд, древнегреческий астроном Гиппарх (II в. до н. э.) составил первые тригонометрические таблицы.
Понятия синуса и косинуса появляются в тригонометрических трактатах индийских ученых в IV-V вв. н. э. В X в. арабские ученые оперировали понятием тангенса, которое возникло из потребностей гномоники — учения о солнечных часах (рис. 4.5).

В Европе первой работой, в которой тригонометрия рассматривалась как отдельная наука, был трактат «Пять книг о треугольниках всех видов», впервые напечатанный в 1533 г. Его автором был немецкий ученый Региомонтан (1436-1476). Этот же ученый открыл и теорему тангенсов:
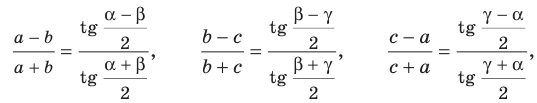
где 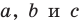 — длины сторон треугольника,
— длины сторон треугольника, 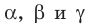 — величины углов треугольника, противолежащих соответственно сторонам с длинами
— величины углов треугольника, противолежащих соответственно сторонам с длинами 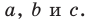
Современный вид тригонометрия приобрела в работах великого математика Леонарда Эйлера.
Леонард Эйлер

(1707-1783) Выдающийся математик, физик, механик и астроном, автор более 860 научных работ. Член Петербургской, Берлинской, Парижской академий наук, Лондонского королевского общества, многих других академий и научных обществ. Имя Эйлера встречается почти во всех областях математики: теоремы Эйлера, тождества Эйлера, углы, функции, интегралы, формулы, уравнения, подстановки и т. д.
Формулы для нахождения площади треугольника
Из курса геометрии 8 класса вы знаете, что площадь 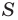 треугольника со сторонами
треугольника со сторонами 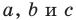 и высотами
и высотами 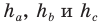 можно вычислить по формулам
можно вычислить по формулам
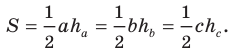
Теперь у нас появилась возможность получить еще несколько формул для нахождения площади треугольника.
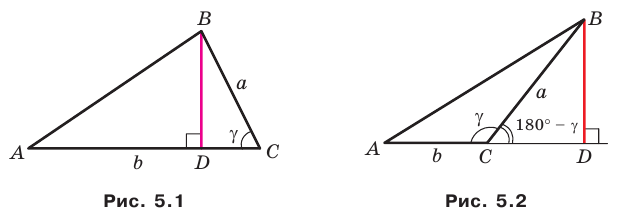
Теорема 5.1. Площадь треугольника равна половине произведения двух его сторон и синуса угла между ними.
Доказательство: Рассмотрим треугольник 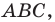 площадь которого равна
площадь которого равна 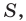 такой, что
такой, что 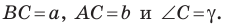 Докажем, что
Докажем, что
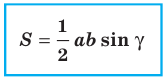
Возможны три случая:
- угол
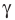 острый (рис. 5.1);
острый (рис. 5.1); - угол
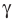 тупой (рис. 5.2);
тупой (рис. 5.2); - угол
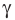 прямой.
прямой.
На рисунках 5.1 и 5.2 проведем высоту 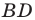 треугольника
треугольника 
Тогда 
Из прямоугольного треугольника 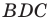 в первом случае (см. рис. 5.1) получаем:
в первом случае (см. рис. 5.1) получаем: 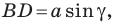 а во втором (см. рис. 5.2):
а во втором (см. рис. 5.2): 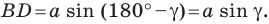 Отсюда для двух первых случаев имеем:
Отсюда для двух первых случаев имеем:
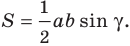
Если угол 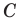 прямой, то
прямой, то 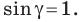 Для прямоугольного треугольника
Для прямоугольного треугольника  с катетами
с катетами 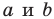 имеем:
имеем:
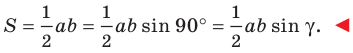
Теорема 5.2 (формула Герона - Площадь
- Площадь 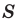 треугольника со сторонами
треугольника со сторонами 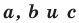 можно вычислить по формуле
можно вычислить по формуле
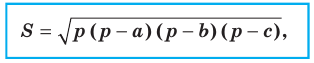
где 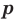 — его полупериметр.
— его полупериметр.
Доказательство: Рассмотрим треугольник 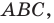 площадь которого равна
площадь которого равна 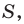 такой, что
такой, что 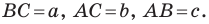 Докажем, что
Докажем, что
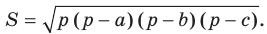
Пусть 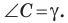 Запишем формулу площади треугольника:
Запишем формулу площади треугольника:
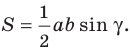 Отсюда
Отсюда 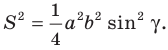
По теореме косинусов 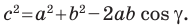 Тогда
Тогда 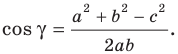
Поскольку 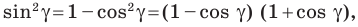 то:
то:
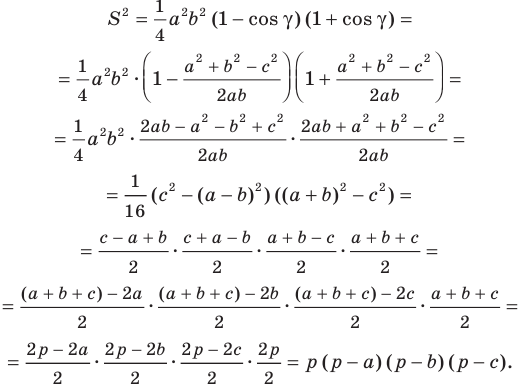
Отсюда 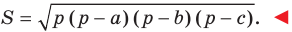
Теорема 5.3. Площадь 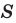 треугольника со сторонами
треугольника со сторонами 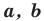 и
и 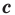 можно вычислить по формуле
можно вычислить по формуле
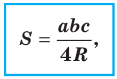
где 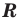 — радиус окружности, описанной около треугольника.
— радиус окружности, описанной около треугольника.
Доказательство: Рассмотрим треугольник 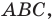 площадь которого равна
площадь которого равна 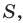 такой, что
такой, что 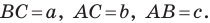 Докажем, что
Докажем, что 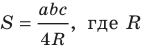 — радиус описанной окружности треугольника.
— радиус описанной окружности треугольника.
Пусть 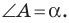 Запишем формулу площади треугольника:
Запишем формулу площади треугольника:
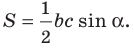
Из леммы п. 3 следует, что 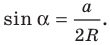
Тогда 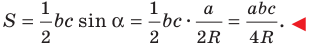
Заметим, что доказанная теорема позволяет находить радиус описанной окружности треугольника по формуле
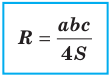
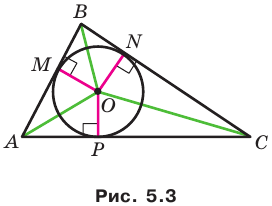
Теорема 5.4. Площадь треугольника равна произведению его полупериметра и радиуса вписанной окружности.
Доказательство: На рисунке 5.3 изображен треугольник 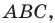 в который вписана окружность радиуса
в который вписана окружность радиуса 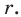 Докажем, что
Докажем, что
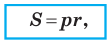
где 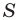 — площадь данного треугольника,
— площадь данного треугольника, 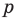 — его полупериметр.
— его полупериметр.
Пусть точка 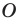 — центр вписанной окружности, которая касается сторон треугольника
— центр вписанной окружности, которая касается сторон треугольника 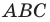 в точках
в точках 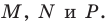 Площадь треугольника
Площадь треугольника 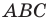 равна сумме площадей треугольников
равна сумме площадей треугольников 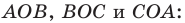
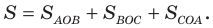
Проведем радиусы в точки касания. Получаем: 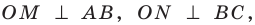
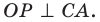 Отсюда:
Отсюда:
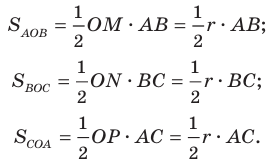
Следовательно,
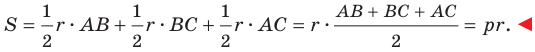
Теорему 5.4 обобщает следующая теорема.
Теорема 5.5. Площадь описанного многоугольника равна произведению его полупериметра и радиуса вписанной окружности.
Докажите эту теорему самостоятельно (рис. 5.4).
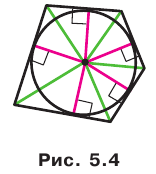
Заметим, что теорема 5.5 позволяет находить радиус вписанной окружности многоугольника по формуле
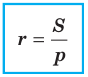
Пример №15
Докажите, что площадь 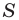 параллелограмма можно вычислить по формуле
параллелограмма можно вычислить по формуле
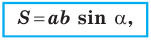
где 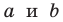 — длины соседних сторон параллелограмма,
— длины соседних сторон параллелограмма, 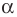 — угол между ними.
— угол между ними.
Решение:
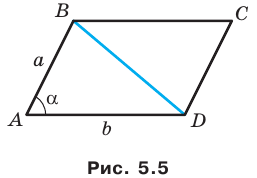
Рассмотрим параллелограмм 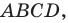 в котором
в котором 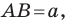
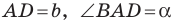 (рис. 5.5). Проведем диагональ
(рис. 5.5). Проведем диагональ 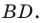 Поскольку
Поскольку 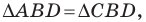 то запишем:
то запишем:
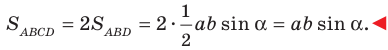
Пример №16
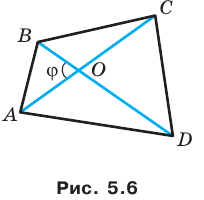
Докажите, что площадь выпуклого четырехугольника равна половине произведения его диагоналей и синуса угла между ними.
Решение:
Пусть угол между диагоналями  четырехугольника
четырехугольника  равен
равен 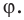 На рисунке 5.6
На рисунке 5.6  Тогда
Тогда  Имеем:
Имеем:
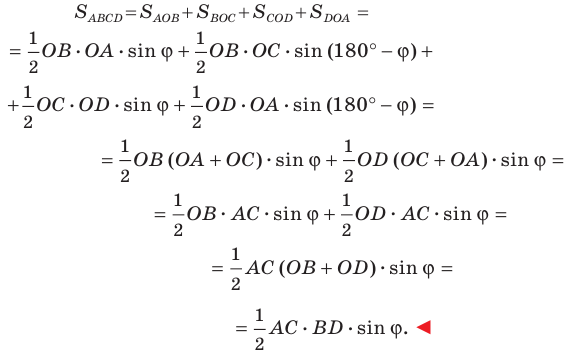
Пример №17
Стороны треугольника равны 17 см, 65 см и 80 см. Найдите наименьшую высоту треугольника, радиусы его вписанной и описанной окружностей.
Решение:
Пусть 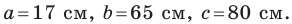
Найдем полупериметр треугольника:
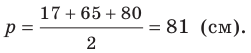
Площадь треугольника вычислим по формуле Герона:
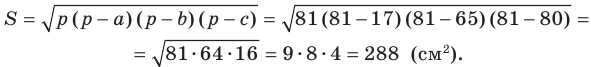
Наименьшей высотой треугольника является высота, проведенная к его наибольшей стороне, длина которой равна 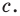
Поскольку 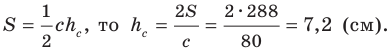
Радиус вписанной окружности
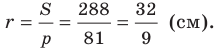
Радиус описанной окружности
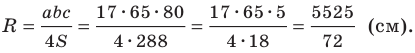
Ответ: 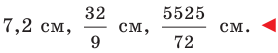
Вневписанная окружность треугольника
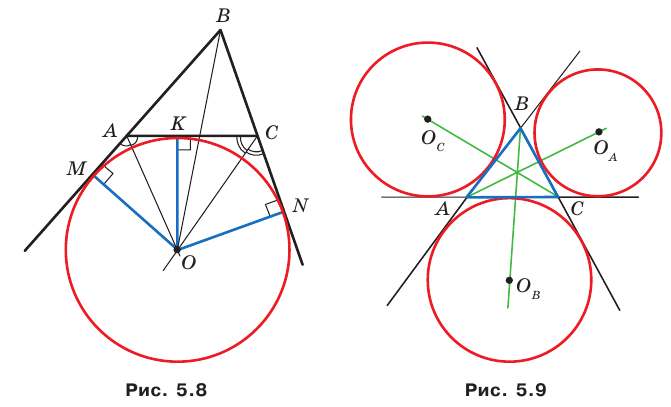
Проведем биссектрисы двух внешних углов с вершинами 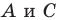 треугольника
треугольника 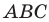 (рис. 5.8). Пусть
(рис. 5.8). Пусть 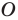 — точка пересечения этих биссектрис. Тогда точка
— точка пересечения этих биссектрис. Тогда точка 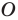 равноудалена от прямых
равноудалена от прямых 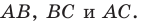
Проведем три перпендикуляра: 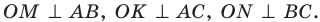 Очевидно, что
Очевидно, что 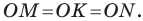 Следовательно, существует окружность с центром в точке
Следовательно, существует окружность с центром в точке  которая касается стороны треугольника и продолжений двух других его сторон. Такую окружность называют вневписанной окружностью треугольника
которая касается стороны треугольника и продолжений двух других его сторон. Такую окружность называют вневписанной окружностью треугольника 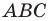 (рис. 5.8).
(рис. 5.8).
Поскольку 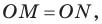 то точка
то точка 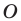 принадлежит биссектрисе угла
принадлежит биссектрисе угла 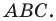
Любой треугольник имеет три вневписанные окружности. На рисунке 5.9 их центры обозначены 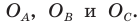 Радиусы этих окружностей обозначим соответственно
Радиусы этих окружностей обозначим соответственно 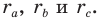
По свойству касательных, проведенных к окружности через одну точку, имеем: 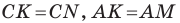 (рис. 5.8). Тогда
(рис. 5.8). Тогда 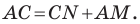 Следовательно, периметр треугольника
Следовательно, периметр треугольника 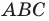 равен сумме
равен сумме 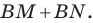 Однако
Однако 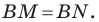 Тогда
Тогда 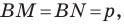 где
где 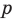 — полупериметр треугольника
— полупериметр треугольника 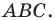
Имеем:
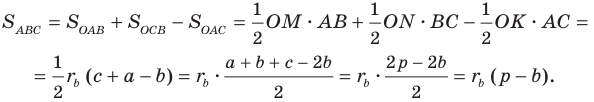
Отсюда 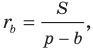 где
где 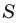 — площадь треугольника
— площадь треугольника 
Аналогично можно показать, что 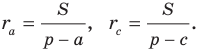
Справочный материал
Косинус и синус
Косинусом и синусом угла 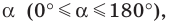 которому соответствует точка
которому соответствует точка 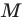 единичной полуокружности, называют соответственно абсциссу и ординату точки
единичной полуокружности, называют соответственно абсциссу и ординату точки 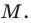
Тангенс
Тангенсом угла 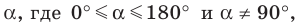 называют отношение
называют отношение 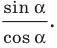
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса угла между ними: 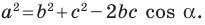
Следствие из теоремы косинусов
Пусть 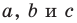 — длины сторон треугольника, причем
— длины сторон треугольника, причем 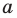 — длина его наибольшей стороны. Если
— длина его наибольшей стороны. Если 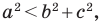 то треугольник является остроугольным. Если
то треугольник является остроугольным. Если 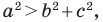 то треугольник является тупоугольным. Если
то треугольник является тупоугольным. Если 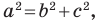 то треугольник является прямоугольным.
то треугольник является прямоугольным.
Лемма о хорде окружности
Хорда окружности равна произведению диаметра и синуса любого вписанного угла, опирающегося на эту хорду.
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов:
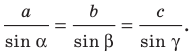
Формулы для нахождения площади треугольника
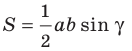
Формула Герона: 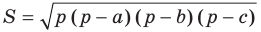
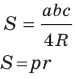
Формула для нахождения радиуса окружности, вписанной в треугольник
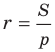
Формулы для нахождения радиуса окружности, описанной около треугольника
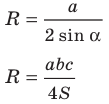
Площадь многоугольника, описанного около окружности
Площадь многоугольника, описанного около окружности, равна произведению его полупериметра и радиуса вписанной окружности.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |