Релятивистская механика в физике - формулы и определение с примерами

Содержание:

Релятивистская механика:

Принято считать, что современная физика начала свое развитие на рубеже XIX и XX в. Одним из толчков, способствующих ее становлению, было формирование в 1905 г. выдающимся ученым-физиком Альбертом Эйнштейном специальной теории относительности (сокращенно СТО), которая развила фундаментальные понятия классической физики, в частности представление о пространстве и времени. Современная механика, которую называют также релятивистской, построена на фундаменте теории относительности, которая объясняет явления и процессы физического мира на основании единства пространства и времени.

Эйнштейн Альберт (1879-1955) - выдающийся физик-теоретик, лауреат Нобелевской премии (1921), один из основателей современной физики, создатель теории относительности. Ввел понятие фотона как кванта света, на основании квантовых представлений объяснил явление фотоэффекта, вывел формулу взаимосвязи между массой и энергией, развил молекулярно-статистическую теорию броуновского движения, сделал много других теоретических открытий, предположений и обобщений в современной физике и астрономии. Ему принадлежит решающая роль в популяризации физических знаний и введении в науку таких новых физических теорий, как общая и специальная теория относительности, квантовая теория фотоэффекта, теория рассеивания света и т. д. Активно выступал против войны, применения ядерного оружия.

Основные положения специальной теории относительности

Основой представлений классической физики о пространстве и времени было их толкование как самостоятельных сущностей, существующих отдельно одна от другой. Т. е. считалось, что время течет само по себе, независимо от особенностей протекания физических явлений и процессов, которые происходят в пространстве; выбор начального момента и интервалов времени является произвольным, независимым от событий, которые предшествовали их ходу, и обстоятельств их протекания. Это означало, что для всех наблюдателей интервалы времени между одними и теми же двумя событиями одинаковые. Как следствие утверждалось, что два события, происходящие одновременно для одного наблюдателя, с неизбежностью будут одновременными и для любого другого.

Классические представления о пространстве определяли его как «вместилище» всего существующего вокруг нас. По своим свойствам оно считалось однородным (в любой точке пространства его свойства остаются одинаковыми) и изотропным, т. е. одинаковым по всем направлениям. Таким образом, классические представления о пространстве и времени предусматривали существование абсолютного, неподвижного пространства и абсолютного, независимого от него времени.

Принцип относительности Г. Галилея утверждает, что законы механики действуют одинаково во всех инерциальных системах отсчета.

На основании такого их понимания Г. Галилей, рассматривая движение корабля, плывущего равномерно и прямолинейно, не изменяя своего движения, высказал предположение, что невозможно выявить никаких изменений в течении механических явлений и установить, движется корабль или он неподвижен, поскольку движение корабля является всеобщим для всего находящегося на нем - людей, предметов, воздуха. Позже данное утверждение он сформулировал как принцип относительности: механические явления и процессы происходят одинаково во всех системах отсчета, движущихся равномерно и прямолинейно. Со временем И. Ньютон положил его в основу классической механики в виде формулировки первого закона механики.

Классические представления о пространстве и времени предоставляли возможность найти удобную систему отсчета, относительно которой было проще описать явления, происходящие в бесконечном эвклидовом пространстве и обыденном измерении времени. Следовательно, классическая теория была способна объяснить довольно обширный круг механических явлений, происходящих вокруг нас. Это движение тел с невысокими скоростями, наблюдаемое людьми в повседневной жизни, космическое движение планет, расчет траекторий искусственных спутников Земли и т. п. Однако когда в начале XX в. физики попытались объяснить природу таких явлений, для которых скорость происходящих событий была соразмерна со скоростью света (электромагнитное излучение, закономерности микромира), то классическая теория оказалась бессильной. Как выяснилось позже, пересмотра требовали сами ее основы, главным образом понятия пространства и времени.

А. Эйнштейн предположил, что принцип относительности Г. Галилея касается не только механических явлений, а распространяется на все физические явления и процессы. Затем он сформулировал постулат, что скорость распространения света не зависит от движения излучающего тела. Эти два утверждения были положены им в основу принципов СТО:

1. во всех инерциальных системах отсчета, независимо от состояния их движения, физические явления происходят по одним и тем же законам;
2. скорость распространения света в вакууме одинакова во всех инерциальных системах отсчета, независимо от их движения, и является предельной в передаче каких-либо взаимодействий.

Предельный характер скорости света в вакууме, независимо от движения излучающего тела, был подтвержден с большой точностью многочисленными физическими экспериментами.

В конце XIX в. американский ученый А. Майкельсон установил, что скорость света в вакууме является неизменяемой величиной во всех инерциальных системах отсчета, независимо от движения излучающего тела. Этот опытный факт, подтвержденный позже многими экспериментами, противоречил закону сложения скоростей

Впервые скорость света измерил в 1676 г. датский астроном О.К. Ремер, наблюдая разницу во времени между затмениями спутников Юпитера. Позже ее значение уточняли многие ученые - английский астроном Дж. Брадлей (1728), французские физики А. И. Я. Физо (1849), Ж. Б. Л. Фуко (1862) и др.

Измеренное А. Майкельсоном в 1926 г. значение скорости света в вакууме с=2,99796 •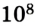

Постулаты СТО, сформулированные А. Эйнштейном, способствовали иному толкованию сущности фундаментальных понятий пространства и времени. Прежде всего они привели к необходимости их объединения в единый континуум -пространство-время. При таких условиях каждому событию, каждому явлению свойственна не только пространственная определенность их местопребывания, но и связанная с ними временная характеристика их осуществления. Это не механическое объединение пространства и времени, когда к системе координат прилагается хронометр, а совместная, объединяющая интерпретация явлений в пространственно-временном измерении. Такое понимание пространства и времени (точнее сказать пространства-времени) привело к изменению сущностных положений физики, в частности одновременности событий, замедление хода часов, уменьшения измеряемой длины.

Континуум (от лат. continuum) - непрерывный, неразрывный.

Относительность одновременности событий

Благодаря тому что в СТО была пересмотрена сущность пространства и времени, оказалось ложным утверждение классической физики об одновременности событий. В классической физике считалось, что события, одновременные в одной инерциальной системе отсчета, будут одновременными и в других таких системах, независимо от их взаимного движения.

Рассмотрим распространение света в подвижной и неподвижной системах отсчета. Пусть в неподвижной системе отсчета находится наблюдатель (рис. 3.1), слева и справа от которого на одинаковом расстоянии l находятся источники света А и В, периодически излучающие световой импульс. В определенный момент времени, зафиксированный часами, находящимися слева, источник света А посылает импульс в направлении наблюдателя. Синхронно такой же импульс излучает источник света В.

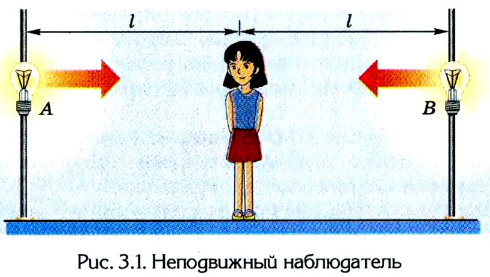
Поскольку расстояние от наблюдателя до источников света одинаковое, то и время распространения светового луча также будет одинаковым, ведь 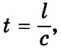а скорость света имеет постоянное значение (с = const). Если наблюдатель принимает импульсы от обоих источников света одновременно, то можно утверждать, что в точках А и В события произошли одновременно.

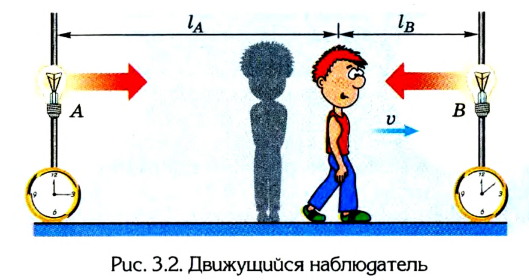
Пусть теперь другой наблюдатель перемещается в направлении одного из источников света, например правого (рис. 3.2). Как выяснилось, теперь получим иной результат. Импульс от источника света В придет к нему раньше, чем от источника А, потому что за время распространения светового импульса наблюдатель приблизится к источнику света В и удалится от источника света A: 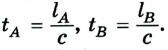Отсюда 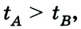потому что 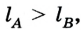а скорость света с - const.

Поэтому для движущегося наблюдателя время прохождения светового импульса от источников А и В будет разным, т. е. события не будут одновременными.

 

Релятивистская механика пересмотрела сложившиеся в классической физике представления о пространстве и времени | как абсолютных субстанциях и интерпретировала их как единый континуум - пространство-время.

Таким образом, можно сделать вывод, что два события, происходящих одновременно в разных точках пространства одной системы отсчета, не будут одновременными в других системах отсчета.

Данное утверждение СТО привело к удивительному выводу, что в подвижных системах отсчета длина сокращается, а время протекания событий замедляется.

Объясняя это, А. Эйнштейн предположил, что при переходе от одной системы отсчета к другой преобразования координат совпадают с формулами преобразований Лоренца:

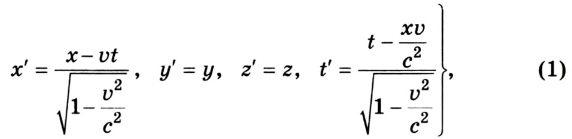
где х, у, z, t - координаты и время в неподвижной системе отсчета, а х', у', z', t' - координаты и время в подвижной системе отсчета.

Поскольку длина определяется разницей координат 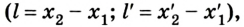то, учитывая формулу (1), получаем:

Это означает, что l'< l, т. е. длина, измеренная в подвижной системе отсчета, меньше длины в системе, относительно которой она движется, ведь множитель в формуле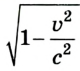 всегда меньше 1.

Стержень длиной 1 м в системе отсчета, которая движется со скоростью, близкой к скорости света в вакууме, например, 0,9 с, сокращает свои размеры приблизительно до 87 см.

В СТО установлено, что измеренная в разных инерциальных системах отсчета продолжительность событий будет неодинаковой.

Пусть в неподвижной системе отсчета некоторое событие продолжается в течение 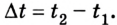Тогда в подвижной системе отсчета его продолжительность будет 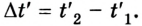Из формул преобразований Лоренца (1) в результате определенных математических упрощений получаем:

Данное соотношение указывает на то, что в подвижной системе отсчета ход события всегда дольше, чем в неподвижной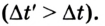

Если проанализировать формулы (2) и (3), то становится очевидным, что при относительно небольших скоростях 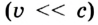подкоренное выражение приблизительно равно 1 и формулы СТО совпадают с формулами классической механики. Сокращение длины, замедление хода часов и другие следствия пространственно-временных свойств физического мира проявляются в том случае, если скорость движения тела близка к скорости света в вакууме.

Таким образом, благодаря более глубокому толкованию свойств пространства и времени в СТО современная физика получила более совершенный инструмент познания природы. Классическая теория (механика Ньютона) присутствует в ней как отдельная система взглядов и теоретических обобщений при определенных условиях и ограничениях (закономерности макромира, незначительные скорости тел по сравнению со скоростью света в вакууме и т. д.).

Взаимосвязь массы и энергии

Согласно законам Ньютона, если на тело действует сила, то оно движется с ускорением. В случае, когда направление действия силы совпадает с направлением движения, то скорость тела должна неограниченно возрастать. Однако данное утверждение противоречит второму принципу СТО, которым скорость передачи взаимодействия ограничивается значением скорости света в вакууме.

Для того чтобы законы Ньютона соблюдались во всех инерциальных системах отсчета, что обусловлено положениями СТО, А. Эйнштейн предложил пересмотреть некоторые классические представления о движении и взаимодействии тел. Прежде всего это касается понятий массы и энергии.

Как известно, масса отражает такие основные свойства тел:

• -    динамическую характеристику тел противодействовать изменению их скорости - так называемая инертная масса, входящая во второй закон механики Ньютона;
• -    способность создавать поле тяготения и взаимодействовать с другими гравитационными полями - так называемая гравитационная масса, входящая в закон всемирного тяготения.

Теоретически установлено и экспериментально подтверждено с достаточно высокой точностью, что инертная и гравитационная массы равны между собой, и поэтому в физике употребляют единое понятие массы, отражающее различные свойства тел. Кроме того, данная физическая величина инвариантна относительно любых инерциальных систем отсчета.

Для того чтобы уравнения релятивистской механики были подобны законам классической механики в любых инерциальных системах отсчета, А. Эйнштейн предположил, что между массой и энергией должна существовать связь. Путем сложных умозаключений и математических преобразований он установил, что масса как физическая величина представляет собой выражение:

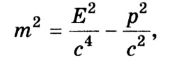
где Е - полная энергия тела, р - его импульс, с - скорость света в вакууме.

Если выбрать такую систему отсчета, в которой скорость тела 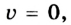то его масса будет равна: 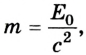т. е. она будет определяться энергией покоя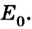

Эта знаменитая формула взаимосвязи массы и энергии является универсальной для всех видов энергии. Она предусматривает, что каждое тело обладает энергией, потенциальный запас которой определяется ее массой: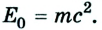

Формула взаимосвязи массы и энергии играет особую роль в атомной и ядерной физике, где преобразование вещества во время ядерных реакций сопровождается значительным высвобождением энергии.

Итоги

Современная механика основывается на постулатах, сформулированных в 1905 г. А. Эйнштейном. В основу СТО им положено два принципа:

1. во всех инерциальных системах отсчета, независимо от состояния их движения, физические явления совершаются по одинаковым законам;
2. скорость распространения света в вакууме является постоянной величиной для всех инерциальных систем отсчета и не зависит от их движения; она представляет собой предельную скорость передачи любого взаимодействия.

Согласно данным утверждениям два события, происходящие одновременно в одной инерциальной системе отсчета, не будут одновременными в других системах отсчета.

Уравнения для преобразования координат совпадают с формулами преобразований Лоренца. Поэтому длина l' в подвижной системе отсчета меньше длины l в системе, относительно которой она движется; продолжительность событий 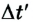в подвижной системе отсчета всегда больше ее продолжительности 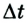в неподвижной системе.

А. Эйнштейн вывел универсальную для всех видов энергии взаимосвязь между массой и энергией: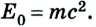

Благодаря более глубокому толкованию свойств пространства и времени современная физика получила более совершенный инструмент познания природы - специальную теорию относительности. Классическая теория в ней представляет собой частичную систему взглядов и обобщений, применимых для познания закономерностей макромира и физических явлений, происходящих при незначительных скоростях тел по сравнению со скоростью света в вакууме.

Элементы специальной теории относительности

«С тех пор как за теорию относительности взялись математики, — признавался А. Эйнштейн, — я ее уже и сам не понимаю». И неудивительно, что вокруг теории относительности вот уже более 100 лет не утихают ожесточенные споры ее «не понимающих». Что послужило причиной создания этого, на первый взгляд, чисто теоретического раздела физики? Оказывается, сначала, почти как всегда в физике, был эксперимент.

Принцип относительности Галилея — Ньютона

Механика — наука о движении. В механике Ньютона любое движение рассматривают относительно инерциальных систем отсчета (СО). Решая задачу, выбирают некую инерциальную СО, условно считая ее неподвижной. Однако это не означает, что выбранная СО — единственно правильная. Можно выбрать любую инерциальную СО — результат будет одинаков.

Для инерциальных СО справедлив механический принцип относительности (принцип относительности Галилея — Ньютона):

Любые механические процессы во всех инерциальных СО происходят одинаково при одинаковых начальных условиях, то есть никакими механическими опытами внутри системы нельзя установить, движется система равномерно прямолинейно или покоится.

В инерциальных СО выполняется классический закон сложения скоростей: скорость 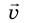движения тела относительно неподвижной СО равна сумме скорости 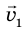движения тела относительно подвижной СО и скорости 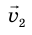движения подвижной СО относительно неподвижной: .

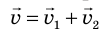Предпосылки создания специальной теории относительности

После того как в середине XIX в. английский физик Джеймс Максвелл (1831–1879) сформулировал основные законы электродинамики, возник вопрос: распространяется ли принцип относительности Галилея — Ньютона на электромагнитные явления? Другими словами: протекают ли электромагнитные процессы (взаимодействие электрических зарядов, распространение электромагнитных волн и т. д.) одинаково во всех инерциальных СО?

Размышления над этим вопросом, казалось бы, сразу приводят к отрицательному ответу. Например, согласно законам электродинамики скорость распространения электромагнитных волн в вакууме, в том числе скорость распространения света, одинакова во всех направлениях и равна 299 792 458 м/с (для расчетов обычно берут округленное значение: c = 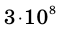м/с). Однако согласно классическому закону сложения скоростей скорость света должна зависеть от выбора СО. Так ли это? Для ответа на этот вопрос американские ученые Альберт Майкельсон (1852–1931) и Эдвард Морли (1838– 1923) в 1887 г. поставили эксперимент.

Идея ученых заключалась в следующем. Если от источника света на Земле направить луч света сначала вдоль линии движения Земли, а затем перпендикулярно ей, то в каждом случае скорость распространения света относительно неподвижной СО должна быть разной. Действительно, согласно классическому закону сложения скоростей скорость 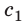света, распространяющегося в направлении движения Земли, должна быть равна:

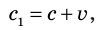
где 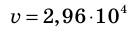м/с — скорость движения Земли вокруг Солнца.

Если свет распространяется в направлении, противоположном направлению движения Земли, то скорость 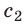его распространения должна быть равна: 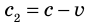. Соответственно скорость 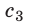света, распространяющегося перпендикулярно направлению движения Земли, должна составлять:

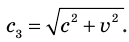
Опыты А. Майкельсона и Э. Морли показали, что скорость распространения света в любом случае одинакова (рис. 24.1). Это поставило в «тупик» ведущих физиков конца XIX — начала ХХ в., ведь полученный результат противоречил классическому закону сложения скоростей.

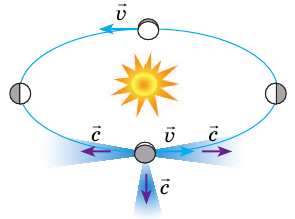
Рис. 24.1. Независимость скорости распространения света от выбора СО. Скорость распространения света вдоль линии движения Земли и перпендикулярно линии ее движения неизменна и равна скорости распространения света в вакууме: 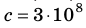м/с.

• Заказать решение задач по физике

Так какая же теория истинна — классическая механика Ньютона или электромагнитная теория Дж. Максвелла? Решением проблемы заинтересовались ведущие физики того времени, среди которых были Хендрик Антон Лоренц (1853–1928), Жюль Анри Пуанкаре (1854–1912), Герман Минковский (1864–1909), Альберт Эйнштейн (1879–1955). Было понятно, что проблему можно решить только на основе новых физических представлений о пространстве и времени. Такие представления начали развиваться еще в конце XIX в., а окончательно были сформулированы А. Эйнштейном в работе «К электродинамике движущихся тел». Независимо друг от друга А. Эйнштейн и Ж. А. Пуанкаре сформулировали важные постулаты, которые легли в основу специальной теории относительности, или релятивистской механики (от лат. relativus — относительный).

Специальная теория относительности (СТО) рассматривает взаимосвязь физических процессов только в инерциальных СО, то есть в СО, которые движутся друг относительно друга равномерно прямолинейно.

Постулаты специальной теории относительности

Первый постулат СТО:

В инерциальных СО все законы природы одинаковы.

Это означает, что все инерциальные СО эквивалентны (равноправны). При наличии двух инерциальных СО нет смысла выяснять, какая из них движется относительно наблюдателя, а какая неподвижна. Никакие опыты в любой области физики (электричество и магнетизм, молекулярная физика, ядерная физика, механика и т. д.) не позволяют выделить абсолютную (предпочтительную) инерциальную СО.

Второй постулат СТО:

Скорость распространения света в вакууме одинакова во всех инерциальных СО.

Это означает, что скорость распространения света в вакууме инвариантна — она не зависит от скорости движения источника или приемника света. Неизменность скорости распространения света — фундаментальное свойство природы. Согласно данному постулату скорость распространения света — максимально возможная скорость распространения любого взаимодействия. Материальные объекты не могут иметь скорость большую, чем скорость света.

Абсолютно ли время:

Кроме скорости света еще одним важнейшим понятием СТО является понятие события.

Событие — любое явление, происходящее в определенной точке пространства в определенный момент времени.

Событие для материальной точки считается заданным, если заданы координаты (x, y, z) места, где событие происходит, и время t, когда это событие происходит. С геометрической точки зрения, задать событие означает задать точку в четырехмерном пространстве «координаты — время».

В классической механике Ньютона время одинаково в любой инерциальной СО, то есть такие понятия, как «сейчас», «раньше», «позже», «одновременно», не зависят от выбора СО. В релятивистской механике время зависит от выбора СО. События, произошедшие в одной СО одновременно, в другой СО могут быть разделены временным промежутком, то есть одновременность двух событий относительна. Покажем это с помощью мысленного эксперимента.

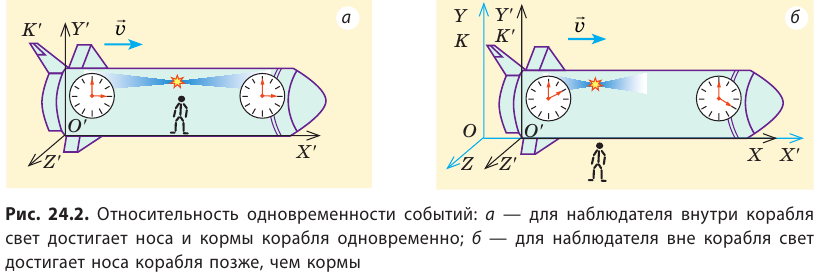
Пусть в центре космического корабля (рис. 24.2), движущегося со скоростью v относительно внешнего наблюдателя, произошла вспышка света. Для наблюдателя, находящегося внутри корабля, свет достигает носа и кормы корабля одновременно, то есть в системе отсчета K′, связанной с кораблем, эти два события происходят одновременно (см. рис. 24.2, а). Для внешнего наблюдателя свет достигает кормы раньше, чем носа корабля, поскольку корма приближается к наблюдателю, а нос корабля удаляется от него, то есть в системе отсчета K, связанной с внешним наблюдателем, эти два события происходят не одновременно (см. рис. 24.2, б).

Релятивистский закон сложения скоростей

Согласно второму постулату СТО скорость света в вакууме постоянна — она не зависит от скорости движения источника или приемника света. Это означает, что классический закон сложения скоростей в релятивистской механике применять нельзя. В СТО применяют релятивистский закон сложения скоростей. Запишем этот закон для частного случая, — случая сложения скоростей, направленных вдоль одной прямой, например вдоль оси OX (рис. 24.3). Тогда релятивистский закон сложения скоростей имеет вид:

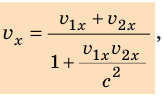
где 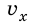— проекция скорости движения тела относительно неподвижной СО K; 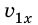— проекция скорости движения тела относительно подвижной СО K′; 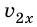— проекция скорости подвижной СО K′ относительно неподвижной СО K. Сравним релятивистский и классический законы сложения скоростей. Если рассматриваемые скорости много меньше скорости света 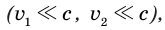то 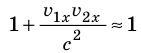и релятивистский закон сложения скоростей принимает вид классического:.

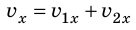Пример решения задачи

Докажите, используя релятивистский закон сложения скоростей, что, если перейти от одной инерциальной системы отсчета к другой, скорость распространения света не изменится.

Решение:

Для решения задачи необходимо выполнить пояснительный рисунок (мы воспользуемся рис. 24.3).

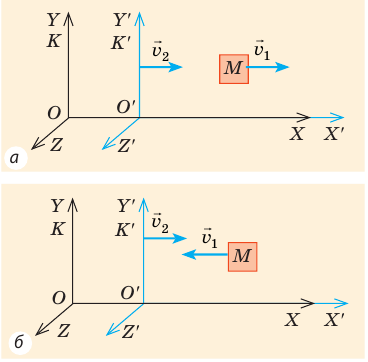
Рис. 24.3. Тело М движется со скоростью 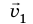относительно СО K′, которая, в свою очередь, движется со скоростью 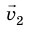относительно СО K: а — направление движения тела совпадает с направлением оси O X′ ′ ; б — направление движения тела противоположно направлению оси O X′ ′

Пусть квант света M движется со скоростью 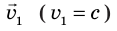вдоль оси O X′ ′ системы отсчета K′, которая, в свою очередь, движется со скоростью 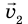в направлении оси OX системы отсчета K. Нам нужно определить скорость кванта относительно системы отсчета K.

Решение. Рассмотрим два случая.

Запишем релятивистский закон сложения скоростей: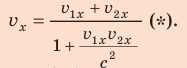

Найдем проекции скорости кванта (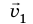) и скорости СО K′ (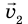) на ось ОХ:

Подставив полученные выражения в формулу (*), имеем:

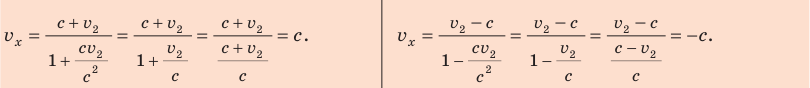
Таким образом, в любом случае скорость кванта света относительно СО K равна с; знак «–» означает, что квант движется в направлении, противоположном направлению оси ОХ.

Ответ: скорость света не зависит от выбора системы отсчета.

Выводы:

• В основе специальной теории относительности (СТО) лежат два постулата: 1) во всех инерциальных СО законы природы одинаковы; 2) скорость распространения света в вакууме одинакова во всех инерциальных СО; это максимально возможная скорость движения и распространения взаимодействия во Вселенной.
• Одновременность двух событий относительна: события, одновременные в одной инерциальной СО, не являются одновременными в инерциальных СО, движущихся относительно первой СО.
• В СТО для определения относительной скорости движения тел применяют релятивистский закон сложения скоростей: 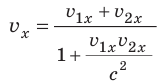. Он принимает вид классического, когда скорости много меньше скорости света. В общем случае классическая механика Ньютона является частным случаем СТО.

Следствия постулатов специальной теории относительности

«Длительность или возраст существования вещей остается одним и тем же независимо от того, быстры движения или медленны, или их нет вообще», — писал И. Ньютон. Создатели классической механики считали очевидным, что и время, и размеры тела абсолютны и не зависят от скорости его движения. Настолько ли это очевидно с точки зрения релятивистской механики?

В чем заключается релятивистский эффект сокращения длины

Длиной стержня называют расстояние между его концами, координаты которых зафиксированы одновременно (по часам той системы, в которой измеряется длина). Поскольку одновременность двух событий относительна, то и длина стержня будет разной в разных СО.

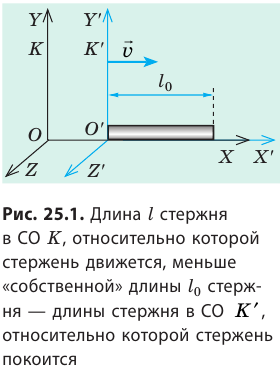
Пусть стержень покоится в СО K′, движущейся с некоторой скоростью v относительно СО K. Если стержень расположен вдоль линии движения системы K′ , то согласно теории относительности имеет место релятивистский эффект сокращения длины (лоренцево сокращение длины) (рис. 25.1):

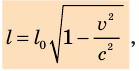
где 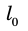— длина стержня в СО K′, относительно которой стержень покоится; l — длина стержня в СО K, относительно которой стержень движется.

Обратите внимание!

1. Размеры тела уменьшаются только вдоль линии его движения: если стержень расположен вдоль линии своего движения, то его длина уменьшается, а вот диаметр остается неизменным.
2. Релятивистский эффект сокращения длины становится заметным только при движении тела со скоростью, сравнимой со скоростью света: даже если ракета движется со второй космической скоростью (v= 11,2 км/с — наименьшая скорость, которую нужно сообщить ракете, чтобы она преодолела притяжение Земли и стала спутником Солнца), то ее длина почти не изменяется; а вот для частицы, разогнанной в ускорителе до скорости v= 0,99с, эффект сокращения длины становится очень заметным.

В чем заключается релятивистский эффект замедления времени

Рассмотрим, как изменяется интервал времени между двумя событиями при переходе от одной инерциальной СО к другой. Для этого воспользуемся световым часами — стержнем длиной 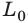, на концах которого (перпендикулярно стержню) закреплены два зеркала (см. рис. 25.2, а). Световой импульс движется от одного зеркала к другому, и каждое отражение импульса от зеркала фиксируется.

Наблюдатель, относительно которого часы находятся в покое, заметит, что время между двумя последовательными отражениями равно: 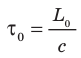. Для наблюдателя, относительно которого часы движутся с некоторой скоростью v , световой импульс пройдет расстояние 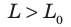(рис. 25.2, б), поэтому этот наблюдатель зафиксирует другое время между двумя отражениями: 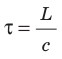. По теореме Пифагора: 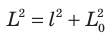, или:

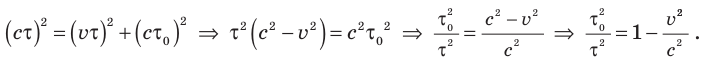
Отсюда время τ, измеренное наблюдателем, относительно которого часы движутся, равно:

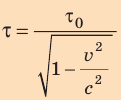
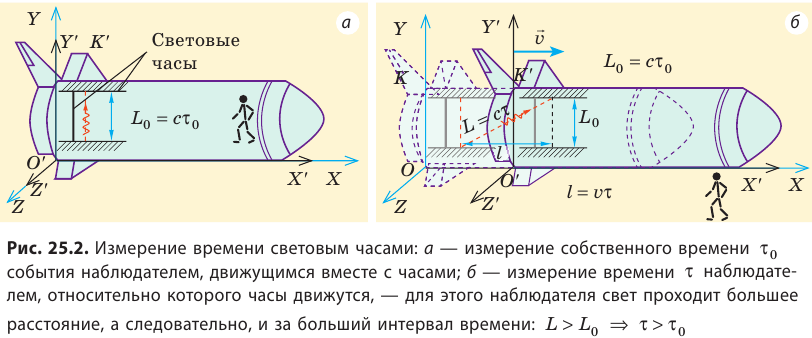
Интервал времени 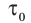, отсчитываемый в СО, относительно которой часы находятся в состоянии покоя (собственное время события), меньше, чем интервал времени τ, отсчитываемый в СО, относительно которой часы движутся. Другими словами, время в движущейся СО замедляется.

Обратите внимание! Замедление времени покажут любые часы в подвижной СО. Эффект замедления времени — свойство самого времени. В подвижной СО замедляются все физические процессы, замедляется и процесс старения.

Замедление времени экспериментально наблюдается, например, при радиоактивном распаде ядер. Пусть в СО, относительно которой ядро покоится, среднее время жизни ядра равно 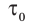= 0,1 с. Если с помощью ускорителя разогнать ядро до такой скорости, что 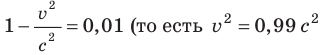), среднее время жизни ядра составит: .

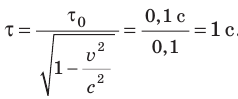Таким образом, с точки зрения неподвижного наблюдателя ускоренные ядра радио активных веществ живут (не распадаются) в среднем дольше, чем такие же ядра в состоянии покоя.

«Парадокс близнецов»:

Для наглядности замедления темпов процессов в системах, движущихся с большими скоростями, А. Эйнштейн предложил яркий мысленный эксперимент.

Посадим одного из близнецов в ракету и разгоним ее до скорости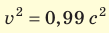. Вернем его на Землю через один год по часам, работающим в ракете: 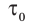= 1 год. Часы на Земле покажут, что между двумя событиями — отлетом и прибытием ракеты — прошло: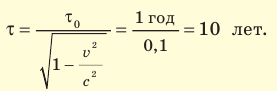

Таким образом, близнец, оставшийся на Земле, состарится больше, чем близнец, летевший в ракете со скоростью, близкой к скорости света. Сделаем важное замечание: СТО рассматривает только инерциальные СО.

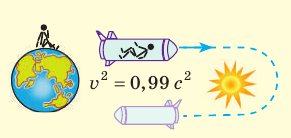
СО, связанная с ракетой, которая улетает с Земли и затем на нее возвращается, не является инерциальной: ракета не менее трех раз ускоряется — при отлете, при развороте и при посадке. По этой причине непосредственно применять формулу замедления времени для ситуации с близнецами нельзя. Ее необходимо рассматривать методами общей теории относительности (ОТО). Отметим, что в ОТО «парадокс близнецов» сохраняется.

Как связаны масса и энергия

Один из важнейших результатов СТО — установление связи энергии E тела с его массой: если тело массой m движется со скоростью v относительно некоторой СО, то энергия E тела в этой СО равна:

(*)

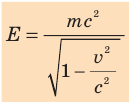Эта формула прошла проверку в экспериментах по ускорению ядер, протонов, электронов. Из нее следует несколько важных следствий.

1. Любое тело (любая частица), имеющее массу, несет с собой запас энергии. Действительно, даже если скорость тела (частицы) уменьшается до нуля (v= 0), согласно формуле (*) тело все равно обладает энергией, — энергией покоя:

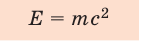
2. Изменение энергии тела прямо пропорционально изменению его массы: 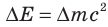. Передача неподвижном телу энергии всегда сопровождается увеличением его массы, и наоборот: выделение телом энергии сопровождается уменьшением его массы. Например, если тело нагревают, его масса увеличивается, а когда охлаждают, его масса уменьшается.

В полной мере формулу связи энергии и массы оценили в 1940-х гг., когда создавали атомную бомбу. Дело в том, что ядро Урана-235 распадается после захвата им медленного нейтрона, в результате чего выделяется энергия. Расчеты показали, что суммарная масса ядра Урана и нейтрона больше, чем общая масса частиц, которые образуются после распада. Этот дефект массы (∆m) и выделяется в виде энергии.

3. В случаях, когда тело (частица) движется со скоростью много меньшей, чем скорость света ( v << с), формулу (*) можно записать так:

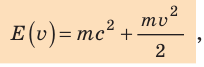
где 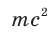— энергия покоя; 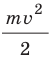— кинетическая энергия тела (частицы).

Выводы:

• Длина тела в разных СО различна. Наибольшую длину тело имеет в той СО, относительно которой оно покоится.
• Время в разных СО течет с разной скоростью. В подвижных СО время течет медленнее, чем в неподвижных.
• Энергия тела (частицы) связана с его (ее) массой и зависит от скорости v его (ее) движения: 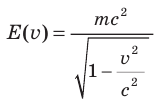. Если v= 0, то 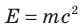— энергия покоя тела (частицы).