Развертка поверхности призмы в начертательной геометрии с примером

Развертка поверхности призмы:

При построении развертки поверхности любого многогранника все его грани располагают в одной плоскости. В результате построения развертки получают плоскую фигуру, в которой все грани многогранника сохраняют свою форму, натуральные размеры и последовательность расположения. Рассмотрим построение развертки поверхности пятиугольной призмы (рис. 5.9.).

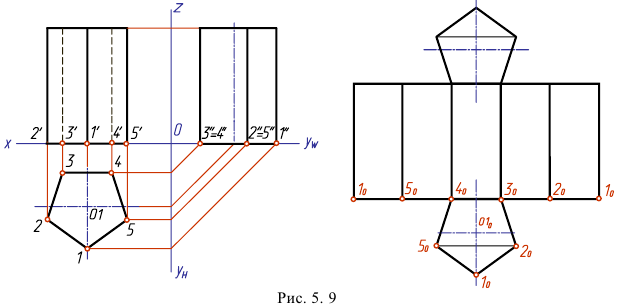
Для построения развертки боковой поверхности проводим горизонтальную прямую линию, на которой откладываем пять отрезков, каждый из которых равен ширине грани или стороне пятиугольного основания. Можно взять величину этого отрезка с ортогонального чертежа, где сторона основания проецируется без искажения. Получаем точки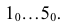

Далее строим два основания. Для этого через середину стороны грани 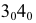(или любой другой) проводим центровую линию, на которую с горизонтальной проекции переносим расстояние от стороны 34 до центра 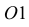и вершины основания. Строим точку 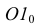и проводим вторую центровую линию основания. Для нахождения точек 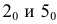на горизон­тальной проекции точки 2 и 5 соединяем прямой линией. Измеряем расстояние от точки пересечения этой линии с центровой до стороны 34 и переносим это расстояние на соответствующую центровую линию на развертке. Проводим параллельно стороне 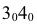прямую, на которую с горизонтальной проекции переносим расстояние от осевой линии до точек 2 и 5. Полученные точки 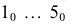соединяем отрезками, получаем основание. Таким же образом строим второе основание.

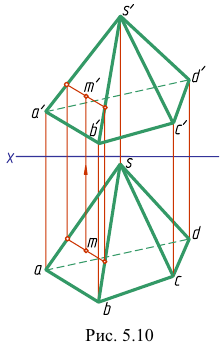
Пирамида представляет собой много­гранник (рис. 5.10), у которого одна грань - основание (произвольный многоугольник ABCD). Остальные грани (боковые) - тре­угольники с общей вершиной S. называемой вершиной пирамиды. Для задания на чертеже пирамиды дос­таточно задать ее основание и вершину. Чтобы построить проекции точки на поверхности пирамиды, нужно через эту точку провести прямую, аналогично построению, выполненному на рис. 5.8, б для призмы.